“Coupling Conduction, Convection and Radiative Transfer in a Single Path-Space: Application to Infrared Rendering” by Bati, Blanco, Coustet, Eymet, Forest, et al. …
Conference:
Type(s):
Title:
- Coupling Conduction, Convection and Radiative Transfer in a Single Path-Space: Application to Infrared Rendering
Session/Category Title:
- Pushing the Boundaries
Presenter(s)/Author(s):
- Mégane Bati
- Stéphane Blanco
- Christophe Coustet
- Vincent Eymet
- Vincent Forest
- Richard Fournier
- Jacques Gautrais
- Nicolas Mellado
- Mathias Paulin
- Benjamin Piaud
Moderator(s):
Abstract:
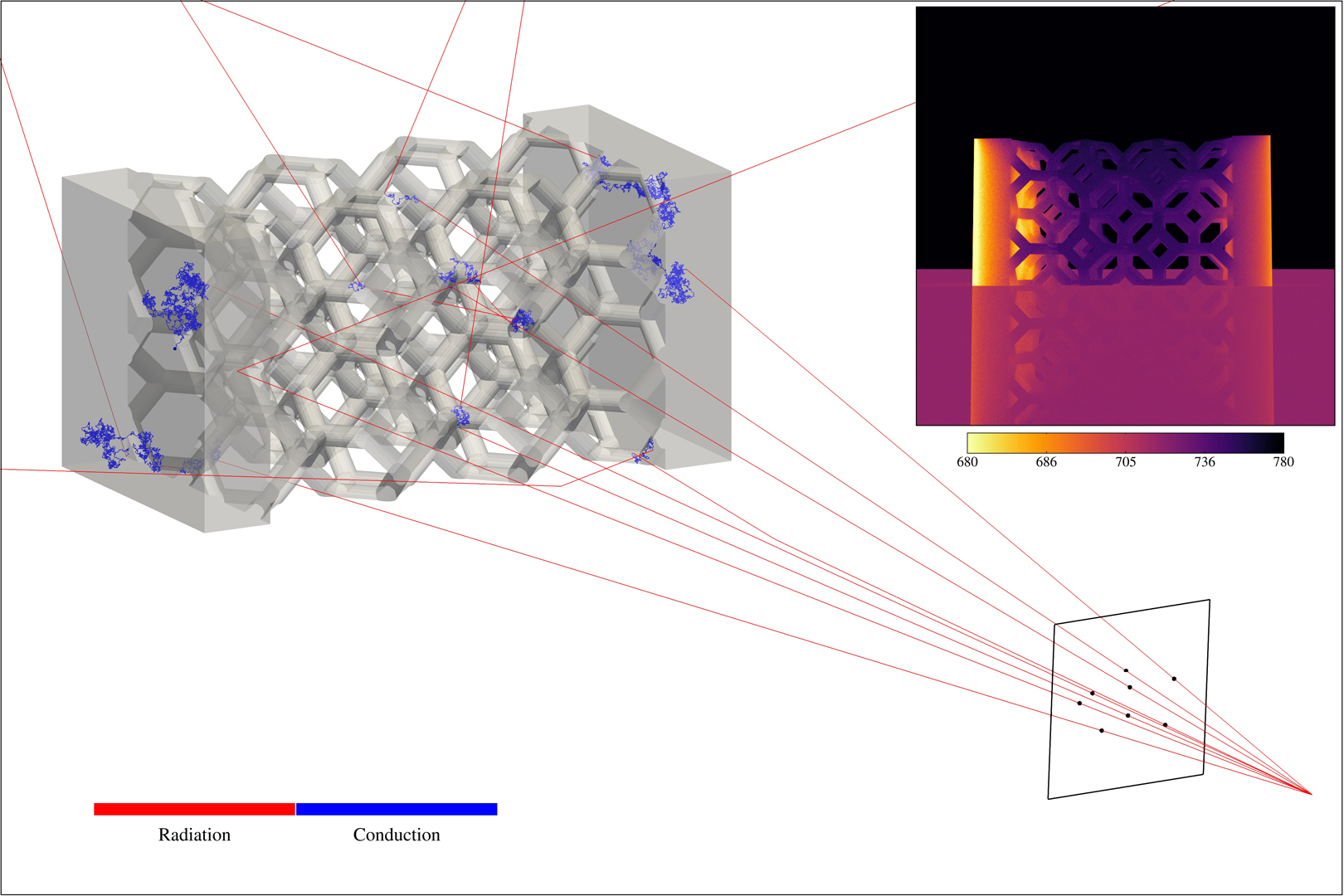
In the past decades, Monte Carlo methods have shown their ability to solve PDEs, independently of the dimensionality of the integration domain and for different use-cases (e.g. light transport, geometry processing, physics simulation). Specifically, the path-space formulation of transport equations is a key ingredient to define tractable and scalable solvers, and we observe nowadays a strong interest in the definition of simulation systems based on Monte Carlo algorithms. We also observe that, when simulating combined physics (e.g. thermal rendering from a heat transfer simulation), there is a lack of coupled Monte Carlo algorithms allowing to solve all the physics at once, in the same path space, rather than combining several independent MC estimators, a combination that would make the global solver critically sensitive to the complexity of each simulation space. This brings to our proposal: a coupled, single path-space, Monte Carlo algorithm for efficient multi-physics problems solving.In this work, we combine our understanding and knowledge of Physics and Computer Graphics to demonstrate how to formulate and arrange different simulation spaces into a single path space. We define a tractable formalism for coupled heat transfer simulation using Monte Carlo, and we leverage the path-space construction to interactively compute multiple simulations with different conditions in the same scene, in terms of boundary conditions and observation time. We validate our proposal in the context of infrared rendering with different thermal simulation scenarios: e.g., room temperature simulation, visualization of heat paths within materials (detection of thermal bridges), heat diffusion capacity of thermal exchanger. We expect that our theoretical framework will foster collaboration and multidisciplinary studies. The perspectives this framework opens are detailed and we suggest a research agenda towards the resolution of coupled PDEs at the interface of Physics and Computer Graphics.
References:
1. Next Limit 2016. Maxwell Multilight. Next Limit. https://maxwellrender.com
2. ANSYS, Inc. 2017. ANSYS Fluent. ANSYS, Inc. https://www.ansys.com/products/fluids/ansys-fluent
3. Meso-Star 2018. Stardis. Meso-Star. https://www.meso-star.com/projects/stardis/stardis.html
4. Comsol 2020. Comsol Multiphysics®. Comsol. https://www.comsol.com/
5. EDF 2021. SYRTHES. EDF. https://www.edf.fr/en/the-edf-group/inventing-the-future-of-energy/r-d-global-expertise/our-offers/simulation-softwares/syrthes
6. Marco Ament, Christoph Bergmann, and Daniel Weiskopf. 2014. Refractive Radiative Transfer Equation. ACM Trans. Graph. 33, 2, Article 17 (apr 2014), 22 pages.
7. Benedikt Bitterli and Eugene d’Eon. 2022. A Position-Free Path Integral for Homogeneous Slabs and Multiple Scattering on Smith Microfacets. Computer Graphics Forum 41, 4 (2022), 93–104. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.14589
8. Subrahmanyan Chandrasekar. 1960. Radiative Transfer. Dover Publications.
9. Xavier Chermain, Basile Sauvage, Jean-Michel Dischler, and Carsten Dachsbacher. 2020. Procedural Physically-based BRDF for Real-Time Rendering of Glints. Comput. Graph. Forum (Proc. Pacific Graphics) 39, 7 (2020), 243–253.
10. W. A. Coleman. 1968. Mathematical Verification of a Certain Monte Carlo Sampling Technique and Applications of the Technique to Radiation Transport Problems. Nuclear Science and Engineering 32, 1 (1968), 76–81. arXiv:https://doi.org/10.13182/NSE68-1
11. Jérémi Dauchet, Jean-Jacques Bezian, Stéphane Blanco, Cyril Caliot, Julien Charon, Christophe Coustet, Mouna El Hafi, Vincent Eymet, Olivier Farges, Vincent Forest, et al. 2018. Addressing nonlinearities in monte carlo. Scientific reports 8, 1 (2018), 1–11.
12. Jérémi Dauchet, Stéphane Blanco, Jean-François Cornet, Mouna El Hafi, Vincent Eymet, and Richard Fournier. 2013. The practice of recent radiative transfer Monte Carlo advances and its contribution to the field of microorganisms cultivation in photobioreactors. Journal of Quantitative Spectroscopy and Radiative Transfer 128 (2013), 52–59.
13. Madalina Deaconu, Samuel Herrmann, and Sylvain Maire. 2017. The walk on moving spheres: a new tool for simulating Brownian motion’s exit time from a domain. Mathematics and Computers in Simulation 135 (2017), 28–38.
14. Madalina Deaconu and Antoine Lejay. 2006. A random walk on rectangles algorithm. Methodology and Computing in Applied Probability 8, 1 (2006), 135–151.
15. Madalina Deaconu and Antoine Lejay. 2007. Simulation of exit times and positions for Brownian motions and diffusions. In PAMM: Proceedings in Applied Mathematics and Mechanics, Vol. 7. Wiley Online Library, 1081401–1081402.
16. Ivan Dimov and Todor Gurov. 2000. Monte Carlo algorithm for solving integral equations with polynomial non-linearity. Parallel implementation. Pliska Studia Mathematica Bulgarica 13, 1 (2000), 117p–132p.
17. Ivan T Dimov. 2008. Monte Carlo methods for applied scientists. World Scientific.
18. Richard Phillips Feynman and Laurie M Brown. 2005. Feynman’s thesis: a new approach to quantum theory. World Scientific.
19. M. Galtier, S. Blanco, C. Caliot, C. Coustet, J. Dauchet, M. El Hafi, V. Eymet, R. Fournier, J. Gautrais, A. Khuong, B. Piaud, and G. Terrée. 2013. Integral formulation of null-collision Monte Carlo algorithms. Journal of Quantitative Spectroscopy and Radiative Transfer 125 (2013), 57–68.
20. Mathieu Galtier, Stephane Blanco, Jérémi Dauchet, Mouna El Hafi, Vincent Eymet, Richard Fournier, Maxime Roger, Christophe Spiesser, and Guillaume Terrée. 2016. Radiative transfer and spectroscopic databases: A line-sampling Monte Carlo approach. Journal of Quantitative Spectroscopy and Radiative Transfer 172 (2016), 83–97.
21. Victor Gattepaille, Jérémi Dauchet, Fabrice Gros, Matthieu Roudet, Caroline Supplis, and Jean-François Cornet. 2018. Integral formulations of multi-scale models for the optimization of solar photo-catalytic processes. In International Congress/3rd days of GdR Solar Fuels: Artificial photosynthesis and Solar Fuels.
22. Ibón Guillén, Julio Marco, Diego Gutierrez, Wenzel Jakob, and Adrien Jarabo. 2020. A General Framework for Pearlescent Materials. Transactions on Graphics (Proceedings of SIGGRAPH Asia) 39, 6 (Nov. 2020).
23. Yu Guo, Miloš Hašan, and Shuang Zhao. 2018. Position-Free Monte Carlo Simulation for Arbitrary Layered BSDFs. ACM Trans. Graph. 37, 6, Article 279 (dec 2018), 14 pages.
24. John Hammersley. 2013. Monte carlo methods. Springer Science & Business Media.
25. Eric Heitz, Johannes Hanika, Eugene d’Eon, and Carsten Dachsbacher. 2016. Multiple-scattering microfacet BSDFs with the Smith model. ACM Trans. Graph. 35, 4 (July 2016), 58:1–58:14.
26. Nicolas Holzschuch and Romain Pacanowski. 2017. A Two-Scale Microfacet Reflectance Model Combining Reflection and Diffraction. ACM Trans. Graph. 36, 4, Article 66 (jul 2017), 12 pages.
27. John R Howell and Kyle J Daun. 2021. The past and future of the Monte Carlo method in thermal radiation transfer. Journal of Heat Transfer 143, 10 (2021).
28. Chi-Ok Hwang and Michael Mascagni. 2003. Analysis and comparison of Green’s function first-passage algorithms with “Walk on Spheres” algorithms. Mathematics and computers in simulation 63, 6 (2003), 605–613.
29. Kiyosi Itô, P Henry Jr, et al. 1996. Diffusion processes and their sample paths: Reprint of the 1974 edition. Springer Science & Business Media.
30. Wenzel Jakob, Sébastien Speierer, Nicolas Roussel, Merlin Nimier-David, Delio Vicini, Tizian Zeltner, Baptiste Nicolet, Miguel Crespo, Vincent Leroy, and Ziyi Zhang. 2022. Mitsuba 3 renderer. https://mitsuba-renderer.org.
31. Adrian Jarabo, Julio Marco, Adolfo Muñoz, Raul Buisan, Wojciech Jarosz, and Diego Gutierrez. 2014. A Framework for Transient Rendering. ACM Trans. Graph. 33, 6, Article 177 (nov 2014), 10 pages.
32. Mark Kac. 1947. Random walk and the theory of Brownian motion. The American Mathematical Monthly 54, 7P1 (1947), 369–391.
33. Mark Kac et al. 1951. On some connections between probability theory and differential and integral equations. In Proceedings of the second Berkeley symposium on mathematical statistics and probability. The Regents of the University of California.
34. James T. Kajiya. 1986. The Rendering Equation. SIGGRAPH Comput. Graph. 20, 4 (aug 1986), 143–150.
35. Sabelfeld Karl. 2019. First passage Monte Carlo algorithms for solving coupled systems of diffusion-reaction equations. Applied Mathematics Letters 88 (2019), 141–148.
36. Edward A Kopylov and Kirill A Dmitriev. 2000. Light propagation visualization as a tool for 3D scene analysis in lighting design. Computers & Graphics 24, 1 (2000), 31–39.
37. Peter Kutz, Ralf Habel, Yining Karl Li, and Jan Novák. 2017. Spectral and Decomposition Tracking for Rendering Heterogeneous Volumes. ACM Trans. Graph. 36, 4, Article 111 (jul 2017), 16 pages.
38. P Lapeyre, Stéphane Blanco, Cyril Caliot, J Dauchet, Mouna El Hafi, Richard Fournier, Olivier Farges, Jacques Gautrais, and Maxime Roger. 2020. Monte-Carlo and sensitivity transport models for domain deformation. Journal of Quantitative Spectroscopy and Radiative Transfer 251 (2020), 107022.
39. Antoine Lejay and Sylvain Maire. 2010. Simulating diffusions with piecewise constant coefficients using a kinetic approximation. Computer Methods in Applied Mechanics and Engineering 199, 29–32 (2010), 2014–2023.
40. Antoine Lejay and Sylvain Maire. 2013. New Monte Carlo schemes for simulating diffusions in discontinuous media. J. Comput. Appl. Math. 245, 1 (2013), 97–116.
41. Tzu-Mao Li, Miika Aittala, Frédo Durand, and Jaakko Lehtinen. 2018. Differentiable Monte Carlo Ray Tracing through Edge Sampling. ACM Trans. Graph. 37, 6, Article 222 (dec 2018), 11 pages.
42. Sylvain Maire and Giang Nguyen. 2016. Stochastic finite differences for elliptic diffusion equations in stratified domains. Mathematics and Computers in Simulation 121 (2016), 146–165.
43. Julio Marco, Ibón Guillén, Wojciech Jarosz, Diego Gutierrez, and Adrian Jarabo. 2019. Progressive Transient Photon Beams. Computer Graphics Forum 38, 6 (2019), 19–30. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.13600
44. Johannes Meng, Marios Papas, Ralf Habel, Carsten Dachsbacher, Steve Marschner, Markus Gross, and Wojciech Jarosz. 2015. Multi-Scale Modeling and Rendering of Granular Materials. ACM Transactions on Graphics (Proceedings of SIGGRAPH) 34, 4 (July 2015).
45. Mervin E. Muller. 1956. Some Continuous Monte Carlo Methods for the Dirichlet Problem. The Annals of Mathematical Statistics 27, 3 (1956), 569 — 589.
46. Matt Pharr, Wenzel Jakob, and Greg Humphreys. 2016. Physically Based Rendering: From Theory to Implementation (3rd ed.) (3rd ed.). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA. 1266 pages.
47. Yang Qi, Dario Seyb, Benedikt Bitterli, and Wojciech Jarosz. 2022. A bidirectional formulation for Walk on Spheres. Computer Graphics Forum (Proceedings of EGSR) 41, 4 (July 2022).
48. Matthias Raab, Daniel Seibert, and Alexander Keller. 2008. Unbiased Global Illumination with Participating Media. In Monte Carlo and Quasi-Monte Carlo Methods 2006, Alexander Keller, Stefan Heinrich, and Harald Niederreiter (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 591–605.
49. Joël Randrianandrasana, Patrick Callet, and Laurent Lucas. 2021. Transfer Matrix Based Layered Materials Rendering. ACM Trans. Graph. 40, 4, Article 177 (jul 2021), 16 pages.
50. Abdujabbor Rasulov, Gulnora Raimova, and Matyokub Bakoev. 2019. Monte Carlo Solution of Dirichlet Problem for Semi-linear Equation. In Finite Difference Methods. Theory and Applications: 7th International Conference, FDM 2018, Lozenetz, Bulgaria, June 11–16, 2018, Revised Selected Papers 7. Springer, 443–451.
51. Damien Rioux-Lavoie, Ryusuke Sugimoto, Tümay Özdemir, Naoharu H Shimada, Christopher Batty, Derek Nowrouzezahrai, and Toshiya Hachisuka. 2022. A Monte Carlo Method for Fluid Simulation. ACM Transactions on Graphics (TOG) 41, 6 (2022), 1–16.
52. Karl K Sabelfeld. 2019. A global random walk on spheres algorithm for transient heat equation and some extensions. Monte Carlo Methods and Applications 25, 1 (2019), 85–96.
53. Karl K Sabelfeld and Nikita Popov. 2020. Monte Carlo tracking drift-diffusion trajectories algorithm for solving narrow escape problems. Monte Carlo Methods and Applications 26, 3 (2020), 177–191.
54. Karl K Sabelfeld and Dmitrii Smirnov. 2021. A global random walk on grid algorithm for second order elliptic equations. Monte Carlo Methods and Applications 27, 3 (2021), 211–225.
55. Rohan Sawhney and Keenan Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 39, 4, Article 123 (jul 2020), 18 pages.
56. Rohan Sawhney, Bailey Miller, Ioannis Gkioulekas, and Keenan Crane. 2023. Walk on Stars: A Grid-Free Monte Carlo Method for PDEs with Neumann Boundary Conditions. arXiv:2302.11815 [cs.GR]
57. Rohan Sawhney, Dario Seyb, Wojciech Jarosz, and Keenan Crane. 2022. Grid-free Monte Carlo for PDEs with spatially varying coefficients. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1–17.
58. Evan Shellshear and Robin Ytterlid. 2014. Fast distance queries for triangles, lines, and points using SSE instructions. Journal of Computer Graphics Techniques Vol 3, 4 (2014).
59. Shlomi Steinberg, Pradeep Sen, and Ling-Qi Yan. 2022. Towards Practical Physical-Optics Rendering. ACM Trans. Graph. 41, 4, Article 132 (jul 2022), 24 pages.
60. Guillaume Terrée, Mouna El Hafi, Stéphane Blanco, Richard Fournier, Jérémi Dauchet, and Jacques Gautrais. 2022. Addressing the gas kinetics Boltzmann equation with branching-path statistics. Physical Review E 105, 2 (2022), 025305.
61. Jean Marc Tregan, Jean Luc Amestoy, Megane Bati, Jean-Jacques Bezian, Stéphane Blanco, Laurent Brunel, Cyril Caliot, Julien Charon, Jean-Francois Cornet, Christophe Coustet, Louis d’Alençon, Jeremi Dauchet, Sebastien Dutour, Simon Eibner, Mouna El Hafi, Vincent Eymet, Olivier Farges, Vincent Forest, Richard Fournier, Mathieu Galtier, Victor Gattepaille, Jacques Gautrais, Zili He, Frédéric Hourdin, Loris Ibarrart, Jean-Louis Joly, Paule Lapeyre, Pascal Lavieille, MarieHelene Lecureux, Jacques Lluc, Marc Miscevic, Nada Mourtaday, Yaniss Nyffenegger-Péré, Lionel Pelissier, Lea Penazzi, Benjamin Piaud, Clément Rodrigues-Viguier, Gisele Roques, Maxime Roger, Thomas Saez, Guillaume Terrée, Najda Villefranque, Thomas Vourc’h, and Daniel Yaacoub. 2023. Coupling radiative, conductive and convective heat-transfers in a single Monte Carlo algorithm: A general theoretical framework for linear situations. PLOS ONE 18, 4 (04 2023), 1–54.
62. Eric Veach. 1998. Robust Monte Carlo methods for light transport simulation. Stanford University.
63. Delio Vicini, Sébastien Speierer, and Wenzel Jakob. 2021. Path Replay Backpropagation: Differentiating Light Paths using Constant Memory and Linear Time. Transactions on Graphics (Proceedings of SIGGRAPH) 40, 4 (Aug. 2021), 108:1–108:14.
64. Najda Villefranque, Richard Fournier, Fleur Couvreux, Stéphane Blanco, Céline Cornet, Vincent Eymet, Vincent Forest, and Jean-Marc Tregan. 2019. A Path-Tracing Monte Carlo Library for 3-D Radiative Transfer in Highly Resolved Cloudy Atmospheres. Journal of Advances in Modeling Earth Systems 11, 8 (2019), 2449–2473.
65. Najda Villefranque, Frédéric Hourdin, Louis d’Alençon, Stéphane Blanco, Olivier Boucher, Cyril Caliot, Christophe Coustet, Jérémi Dauchet, Mouna El Hafi, Vincent Eymet, Olivier Farges, Vincent Forest, Richard Fournier, Jacques Gautrais, Valéry Masson, Benjamin Piaud, and Robert Schoetter. 2022. The “teapot in a city”: A paradigm shift in urban climate modeling. Science Advances 8, 27 (2022), eabp8934. arXiv:https://www.science.org/doi/pdf/10.1126/sciadv.abp8934
66. Ingo Wald, Sven Woop, Carsten Benthin, Gregory S Johnson, and Manfred Ernst. 2014. Embree: a kernel framework for efficient CPU ray tracing. ACM Transactions on Graphics (TOG) 33, 4 (2014), 1–8.
67. Beibei Wang, Wenhua Jin, Jiahui Fan, Jian Yang, Nicolas Holzschuch, and Ling-Qi Yan. 2022. Position-Free Multiple-Bounce Computations for Smith Microfacet BSDFs. ACM Trans. Graph. 41, 4, Article 134 (jul 2022), 14 pages.
68. A. Wilkie, S. Nawaz, M. Droske, A. Weidlich, and J. Hanika. 2014. Hero Wavelength Spectral Sampling. Computer Graphics Forum 33, 4 (2014), 123–131. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.12419
69. Cheng Zhang, Lifan Wu, Changxi Zheng, Ioannis Gkioulekas, Ravi Ramamoorthi, and Shuang Zhao. 2019. A Differential Theory of Radiative Transfer. ACM Trans. Graph. 38, 6, Article 227 (nov 2019), 16 pages.
70. Shuang Zhao, Wenzel Jakob, and Tzu-Mao Li. 2020. Physics-based differentiable rendering: from theory to implementation. In ACM siggraph 2020 courses. 1–30.
71. Tobias Zirr, Marco Ament, and Carsten Dachsbacher. 2015. Visualization of Coherent Structures of Light Transport. Computer Graphics Forum 34, 3 (2015), 491–500. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.12661