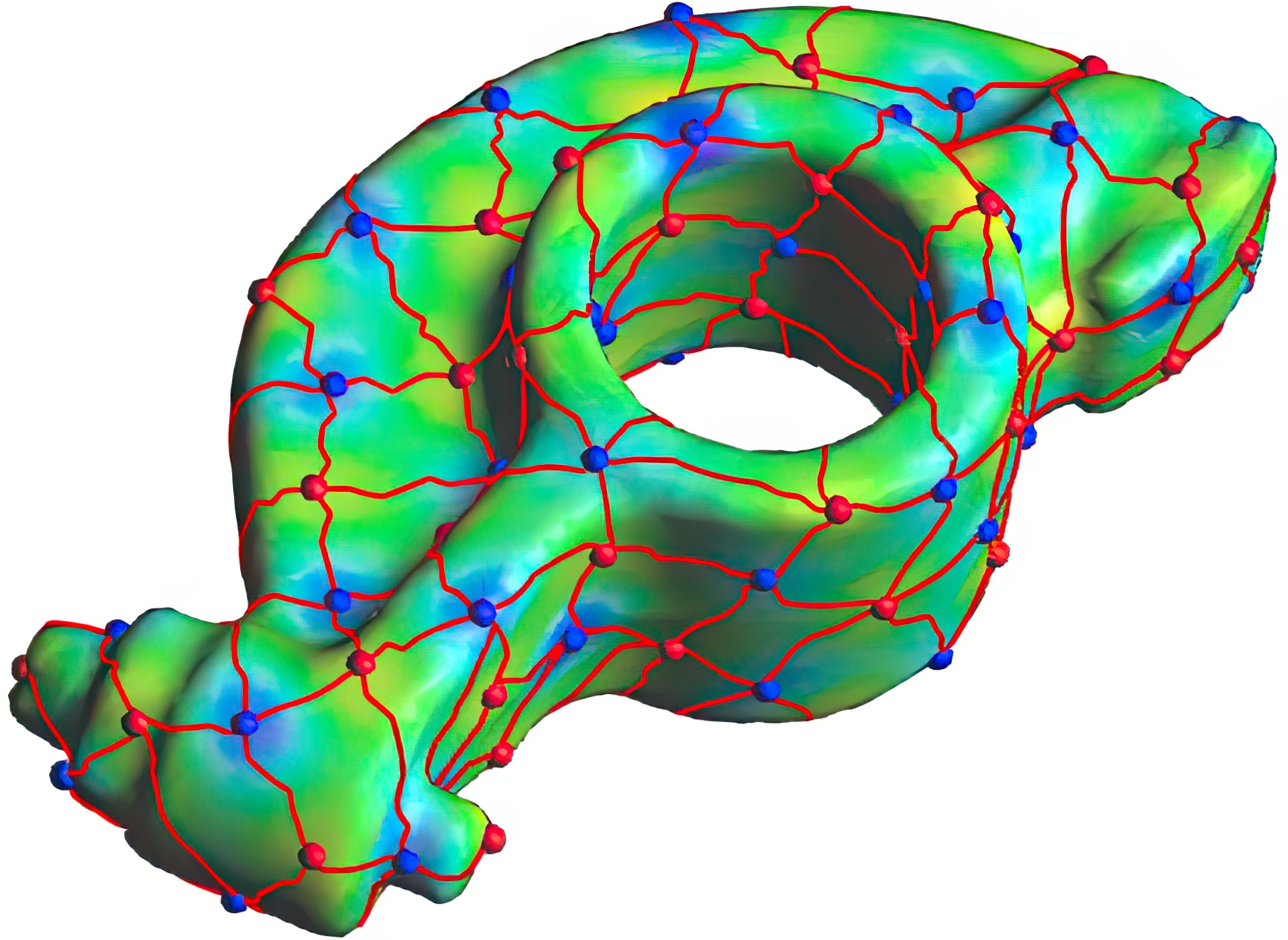
“Spectral quadrangulation with orientation and alignment control”
Conference:
Type(s):
Title:
- Spectral quadrangulation with orientation and alignment control
Session/Category Title: Mesh processing
Presenter(s)/Author(s):
Abstract:
This paper presents a new quadrangulation algorithm, extending the spectral surface quadrangulation approach where the coarse quadrangular structure is derived from the Morse-Smale complex of an eigenfunction of the Laplacian operator on the input mesh. In contrast to the original scheme, we provide flexible explicit controls of the shape, size, orientation and feature alignment of the quadrangular faces. We achieve this by proper selection of the optimal eigenvalue (shape), by adaption of the area term in the Laplacian operator (size), and by adding special constraints to the Laplace eigenproblem (orientation and alignment). By solving a generalized eigen-problem we can generate a scalar field on the mesh whose Morse-Smale complex is of high quality and satisfies all the user requirements. The final quadrilateral mesh is generated from the Morse-Smale complex by computing a globally smooth parametrization. Here we additionally introduce edge constraints to preserve user specified feature lines accurately.
References:
1. Alford, R. M., Kelly, K. R., and Boore, D. M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics 39, 6 (December), 834–842.Google ScholarCross Ref
2. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. ACM Trans. Graph. 22, 3, 485–493. Google ScholarDigital Library
3. Alliez, P., Ucelli, G., Gotsman, C., and Attene, M. 2005. Recent advances in remeshing of surfaces.Google Scholar
4. Boier-Martin, I., Rushmeier, H., and Jin, J. 2004. Parameterization of triangle meshes over quadrilateral domains. In SGP ’04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, ACM, 193–203. Google Scholar
5. Botsch, M., and Pauly, M. 2007. Course 23: Geometric modeling based on polygonal meshes. In SIGGRAPH courses. Google Scholar
6. Davis, T. A. 2004. A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw. 30, 2, 165–195. Google ScholarDigital Library
7. Dong, S., Kircher, S., and Garland, M. 2005. Harmonic functions for quadrilateral remeshing of arbitrary manifolds. Comput. Aided Geom. Des. 22, 5, 392–423. Google ScholarDigital Library
8. Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and Hart, J. C. 2006. Spectral surface quadrangulation. ACM Trans. Graph. 25, 3, 1057–1066. Google ScholarDigital Library
9. Edelsbrunner, H., Letscher, D., and Zomorodian, A. 2002. Topological persistence and simplification. Discrete Computer Geometry 28, 511–533.Google ScholarDigital Library
10. Edelsbrunner, H., Harer, J., and Zomorodian, A. 2003. Hierarchical morse-smale complexes for piecewise linear 2-manifolds. Discrete and Computational Geometry 30, 1, 87–107.Google ScholarCross Ref
11. Fisher, M., Schröder, P., Desbrun, M., and Hoppe, H. 2007. Design of tangent vector fields. In SIGGRAPH ’07: ACM SIGGRAPH 2007 papers, ACM, 56. Google Scholar
12. Gu, X., and Yau, S.-T. 2003. Global conformal surface parameterization. In SGP ’03: Proceedings of the 2003 Eurographics/ACM SIGGRAPH symposium on Geometry processing, Eurographics Association, 127–137. Google ScholarDigital Library
13. Igarashi, T., Moscovich, T., and Hughes, J. F. 2005. As-rigid-as-possible shape manipulation. ACM Trans. Graph. 24, 3, 1134–1141. Google ScholarDigital Library
14. Kälberer, F., Nieser, M., and Polthier, K. 2007. Quadcover — surface parameterization using branched coverings. Computer Graphics Forum 26, 3 (September), 375–384.Google ScholarCross Ref
15. Khodakovsky, A., Litke, N., and Schröder, P. 2003. Globally smooth parameterizations with low distortion. In SIGGRAPH ’03: ACM SIGGRAPH 2003 Papers, ACM, 350–357. Google Scholar
16. Li, W.-C., Ray, N., and Lévy, B. 2006. Automatic and interactive mesh to t-spline conversion. In SGP ’06: Proceedings of the fourth Eurographics symposium on Geometry processing, Eurographics Association, 191–200. Google ScholarDigital Library
17. Marinov, M., and Kobbelt, L. 2004. Direct anisotropic quaddominant remeshing. In PG ’04: Proceedings of the Computer Graphics and Applications, 12th Pacific Conference on (PG’04), IEEE Computer Society, 207–216. Google ScholarDigital Library
18. Marinov, M., and Kobbelt, L. 2006. A robust two-step procedure for quad-dominant remeshing. Computer Graphics Forum 25, 3 (Sept.), 537–546.Google ScholarCross Ref
19. Meyer, M., Desbrun, M., Schröder, P., and Barr, A. H. Discrete differential-geometry operators for triangulated 2-manifolds.Google Scholar
20. Pinkall, U., and Polthier, K. 1993. Computing discrete minimal surfaces and their conjugates. Experimental Mathematics 2, 1, 15–36.Google ScholarCross Ref
21. Ray, N., Li, W. C., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Trans. Graph. 25, 4, 1460–1485. Google ScholarDigital Library
22. Shi, L., and Yu, Y. 2004. Inviscid and incompressible fluid simulation on triangle meshes: Research articles. Comput. Animat. Virtual Worlds 15, 3–4, 173–181. Google ScholarCross Ref
23. Strang, G. 1999. The discrete cosine transform. SIAM Review 41, 1, 135–147. Google ScholarDigital Library
24. Timo Bremer, P., Edelsbrunner, H., Hamann, B., and Pascucci, V. 2004. A topological hierarchy for functions on triangulated surfaces. IEEE Transactions on Visualization and Computer Graphics 10, 385–396. Google ScholarDigital Library
25. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. In SGP ’06: Proceedings of the fourth Eurographics symposium on Geometry processing, Eurographics Association, 201–210. Google ScholarDigital Library
26. Vallet, B., and Lévy, B. 2007. Spectral geometry processing with manifold harmonics. Technical Report (April).Google Scholar
27. Vallet, B., and Lévy, B. 2008. Spectral geometry processing with manifold harmonics. Computer Graphics Forum 27, 2 (Apr.), 251–260.Google ScholarCross Ref
28. Yoshizawa, S., Belyaev, A., and Seidel, H.-P. 2005. Fast and robust detection of crest lines on meshes. In SPM ’05: Proceedings of the 2005 ACM symposium on Solid and physical modeling, ACM, 227–232. Google Scholar