“Sketch-based tree modeling using Markov random field”
Conference:
Type(s):
Title:
- Sketch-based tree modeling using Markov random field
Session/Category Title: Shape modelling
Presenter(s)/Author(s):
Abstract:
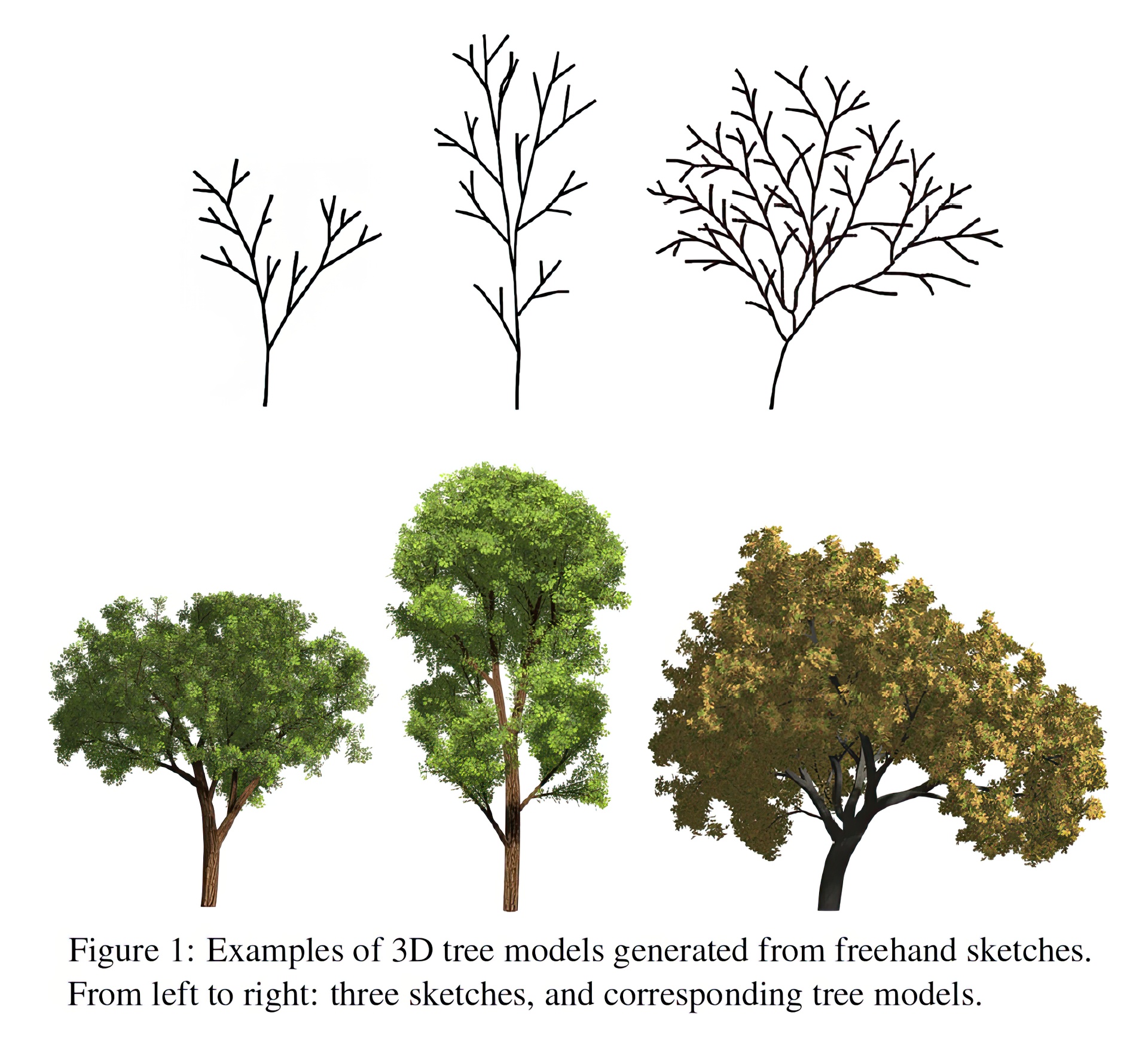
In this paper, we describe a new system for converting a user’s freehand sketch of a tree into a full 3D model that is both complex and realistic-looking. Our system does this by probabilistic optimization based on parameters obtained from a database of tree models. The best matching model is selected by comparing its 2D projections with the sketch. Branch interaction is modeled by a Markov random field, subject to the constraint of 3D projection to sketch. Our system then uses the notion of self-similarity to add new branches before finally populating all branches with leaves of the user’s choice. We show a variety of natural-looking tree models generated from freehand sketches with only a few strokes.
References:
1. Bishop, C. 2006. Pattern Recognition and Machine Learning. Springer. Google Scholar
2. de Reffye, P., Edelin, C., Francon, J., Jaeger, M., and Puech, C. 1988. Plant models faithful to botanical structure and development. In Computer Graphics (SIGGRAPH ’88 Proc.), J. Dill, Ed., vol. 22, ACM SIGGRAPH, 151–158. Google Scholar
3. Holton, M. 1994. Strands, gravity and botanical tree imagery. Computer Graphics Forum 13, 1, 57–67.Google ScholarCross Ref
4. Ijiri, T., Owada, S., and Igarashi, T. 2006. The sketch L-system: Global control of tree modeling using free-form strokes. In Smart Graphics, 138–146.Google Scholar
5. Jirasek, C., Prusinkiewicz, P., and Moulia, B. 2000. Integrating biomechanics into developmental plant models expressed using L-systems. In Proceedings of the 3rd Plant Biomechanics Conference, 615–624.Google Scholar
6. Lamdan, Y., Schwartz, J. T., and Wolfson, H. J. 1988. Object recognition by affine invariant matching. In CVPR, 335–344.Google Scholar
7. Lindenmayer, A. 1968. Mathematical models for cellular interaction in development, parts I and II. Journal of Theoretical Biology 18, 280–315.Google ScholarCross Ref
8. Lintermann, B., and Deussen, O. 1999. Interactive modeling of plants. IEEE Computer Graphics and Applications 19, 1, 56–65. Google ScholarDigital Library
9. Měch, R., and Prusinkiewicz, P. 1996. Visual models of plants interacting with their environment. In SIGGRAPH ’96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, ACM Press, New York, NY, USA, 397–410. Google Scholar
10. Neubert, B., Franken, T., and Deussen, O. 2007. Approximate image-based tree-modeling using particle flows. ACM Trans. Graph. (SIGGRAPH) 26, 3, 88. Google ScholarDigital Library
11. Okabe, M., Owada, S., and Igarashi, T. 2005. Interactive design of botanical trees using freehand sketches and example-based editing. In Computer Graphics Forum, Eurographics 2005, vol. 24.Google Scholar
12. Oppenheimer, P. 1986. Real time design and animation of fractal plants and trees. In Computer Graphics (SIGGRAPH 86 Conf. Proc.), vol. 20, 55–64. Google Scholar
13. Prusinkiewicz, P., Hammel, M., Hanan, J., and Mech, R. 1996. L-systems: from the theory to visual models of plants. In Machine Graphics and Vision, 365–392.Google Scholar
14. Prusinkiewicz, P., Mündermann, L., Karwowski, R., and Lane, B. 2001. The use of positional information in the modeling of plants. In SIGGRAPH ’01: Proceedings of the 28th annual conference on Computer graphics and interactive techniques, ACM Press, New York, NY, USA, 289–300. Google Scholar
15. Reche-Martinez, A., Martin, I., and Drettakis, G. 2004. Volumetric reconstruction and interactive rendering of trees from photographs. ACM Trans. Graph. 23, 3, 720–727. Google ScholarDigital Library
16. Shlyakhter, I., Rozenoer, M., Dorsey, J., and Teller, S. 2001. Reconstructing 3d tree models from instrumented photographs. IEEE Computer Graphics and Applications, 53–61. Google Scholar
17. Tan, P., Zeng, G., Wang, J., Kang, S. B., and Quan, L. 2007. Image-based tree modeling. In SIGGRAPH ’07: ACM SIGGRAPH 2007 papers, ACM, New York, NY, USA, 87. Google Scholar
18. Ulam, S. 1966. Pattern of growth of figures: mathematical aspects. In Module, Proportion, Symmetry, Rhythm, G. Keps, Ed. Braziller, New York, 64–74.Google Scholar
19. Weber, J., and Penn, J. 1995. Creation and rendering of realistic trees. In SIGGRAPH 95 Conf. Proc., 119–128. Google Scholar