“Recursive interlocking puzzles” by Song, Fu and Cohen-Or
Conference:
Type(s):
Title:
- Recursive interlocking puzzles
Session/Category Title:
- Physical Models
Presenter(s)/Author(s):
Abstract:
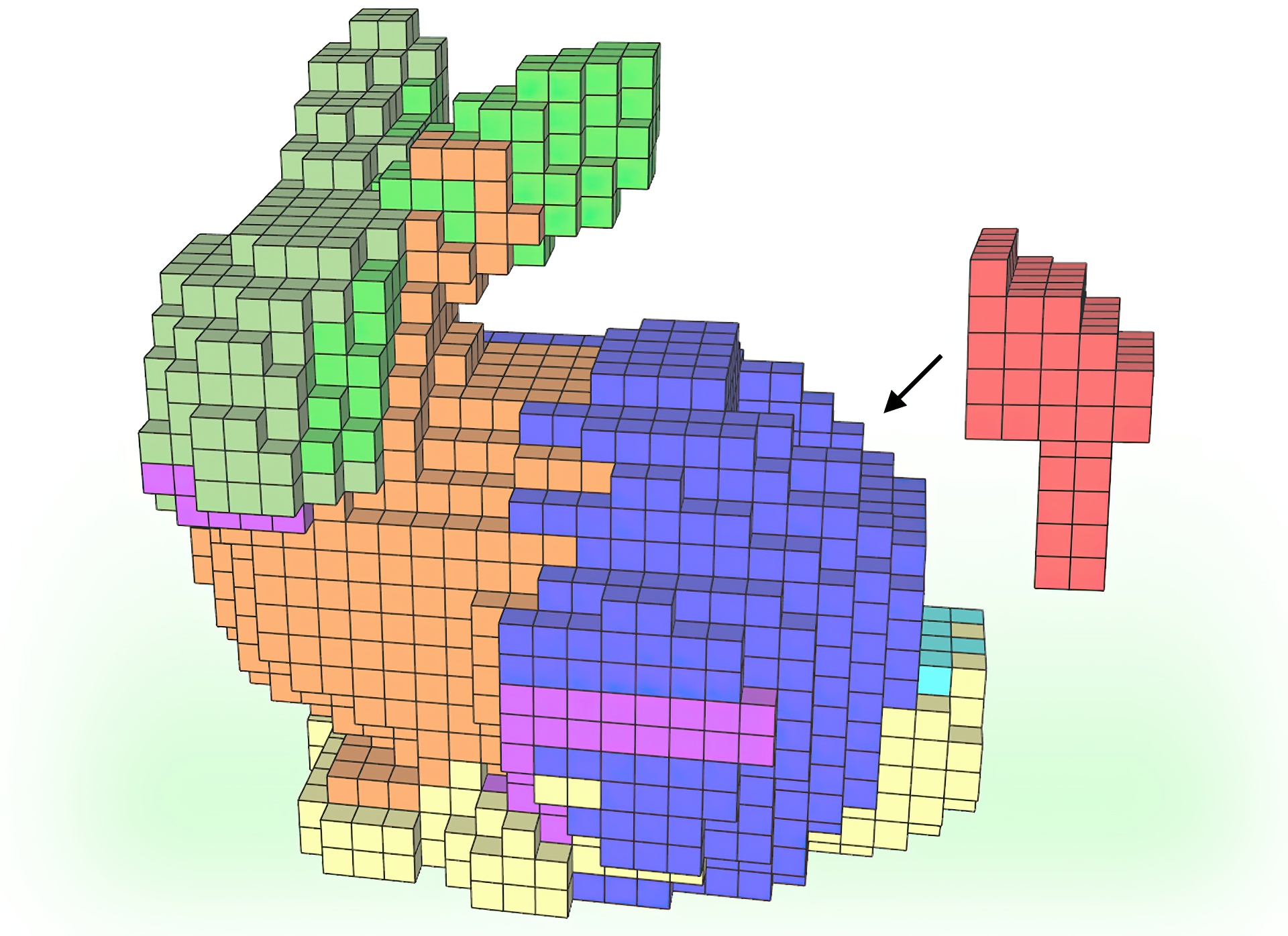
Interlocking puzzles are very challenging geometric problems with the fascinating property that once we solve one by putting together the puzzle pieces, the puzzle pieces interlock with one another, preventing the assembly from falling apart. Though interlocking puzzles have been known for hundreds of years, very little is known about the governing mechanics. Thus, designing new interlocking geometries is basically accomplished with extensive manual effort or expensive exhaustive search with computers.In this paper, we revisit the notion of interlocking in greater depth, and devise a formal method of the interlocking mechanics. From this, we can develop a constructive approach for devising new interlocking geometries that directly guarantees the validity of the interlocking instead of exhaustively testing it. In particular, we focus on an interesting subclass of interlocking puzzles that are recursive in the sense that the assembly of puzzle pieces can remain an interlocking puzzle also after sequential removal of pieces; there is only one specific sequence of assembling, or disassembling, such a puzzle. Our proposed method can allow efficient generation of recursive interlocking geometries of various complexities, and by further realizing it with LEGO bricks, we can enable the hand-built creation of custom puzzle games.
References:
1. Alexa, M., and Matusik, W. 2010. Reliefs as images. ACM Tran. on Graphics (SIGGRAPH) 29, 4. Article 60.
2. Cho, T. S., Avidan, S., and Freeman, W. T. 2010. A probabilistic image jigsaw puzzle solver. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 183–190.
3. Coffin, S. T. 1990. The Puzzling World of Polyhedral Dissections. Oxford University Press.
4. Cutler, W. H. 1978. The six-piece burr. Journal of Recreational Mathematics 10, 4, 241–250.
5. Cutler, W. H., 1994. A computer analysis of all 6-piece burrs. Self published.
6. Freeman, H., and Garder, L. 1964. Apictorial jigsaw puzzles: The computer solution of a problem in pattern recognition. IEEE Transactions on Electronic Computers EC-13, 2, 118–127.
7. Goldberg, D., Malon, C., and Bern, M. 2002. A global approach to automatic solution of jigsaw puzzles. In Proceedings of the Eighteenth Annual ACM Symposium on Computational Geometry, 82–87.
8. Hildebrand, K., Bickel, B., and Alexa, M. 2012. crdbrd: Shape fabrication by sliding planar slices. Computer Graphics Forum (Eurographics) 31, 2, 583–592.
9. Holroyd, M., Baran, I., Lawrence, J., and Matusik, W. 2011. Computing and fabricating multilayer models. ACM Tran. on Graphics (SIGGRAPH ASIA) 30, 6. Article 187.
10. IBM Research, 1997. The burr puzzles site. http://www.research.ibm.com/BurrPuzzles/.
11. Kilian, M., Flöery, S., Chen, Z., Mitra, N. J., Sheffer, A., and Pottmann, H. 2008. Curved folding. ACM Tran. on Graphics (SIGGRAPH) 27, 3.
12. Kong, W., and Kimia, B. B. 2001. On solving 2D and 3D puzzles using curve matching. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), vol. 2, 583–590.
13. Lau, M., Ohgawara, A., Mitani, J., and Igarashi, T. 2011. Converting 3d furniture models to fabricatable parts and connectors. ACM Tran. on Graphics (SIGGRAPH) 30, 4. Article 85.
14. Li, X.-Y., Shen, C.-H., Huang, S.-S., Ju, T., and Hu, S.-M. 2010. Popup: Automatic paper architectures from 3D models. ACM Tran. on Graphics (SIGGRAPH) 29, 3. Article 111.
15. Li, X.-Y., Ju, T., Gu, Y., and Hu, S.-M. 2011. A geometric study of v-style pop-ups: theories and algorithms. ACM Tran. on Graphics (SIGGRAPH) 30, 4. Article 98.
16. Lo, K.-Y., Fu, C.-W., and Li, H. 2009. 3D Polyomino puzzle. ACM Tran. on Graphics (SIGGRAPH Asia) 28, 5. Article 157.
17. Mitani, J., and Suzuki, H. 2004. Making papercraft toys from meshes using strip-based approximate unfolding. ACM Tran. on Graphics (SIGGRAPH) 23, 3, 259–263.
18. Mitra, N. J., and Pauly, M. 2009. Shadow art. ACM Tran. on Graphics (SIGGRAPH Asia) 28, 5. Article 156.
19. Mori, Y., and Igarashi, T. 2007. Plushie: an interactive design system for plush toys. ACM Tran. on Graphics (SIGGRAPH) 26, 3. Article 45.
20. Murakami, T., Toyama, F., Shoji, K., and Miyamichi, J. 2008. Assembly of puzzles by connecting between blocks. In 19th International Conference on Pattern Recognition, 1–4.
21. Röver, A., 2011. Burr tools. http://burrtools.sourceforge.net/.
22. Sagiroglu, M., and Ercil, A. 2006. A texture based matching approach for automated assembly of puzzles. In 18th International Conference on Pattern Recognition, vol. 3, 1036–1041.
23. Seike, K. 1977. Art Of Japanese Joinery. Weatherhill.
24. Tachi, T. 2010. Origamizing polyhedral surfaces. IEEE Transactions on Visualization and Computer Graphics 16, 2, 298–311.
25. Weyrich, T., Deng, J., Barnes, C., Rusinkiewicz, S., and Finkelstein, A. 2007. Digital bas-relief from 3D scenes. ACM Tran. on Graphics (SIGGRAPH) 26, 3. Article 32.
26. Wolfson, H., Schonberg, E., Kalvin, A., and Lamdan, Y. 1988. Solving jigsaw puzzles by computer. Annals of Operations Research 12, 51–64.
27. Xin, S.-Q., Lai, C.-F., Fu, C.-W., Wong, T.-T., He, Y., and Cohen-Or, D. 2011. Making burr puzzles from 3D models. ACM Tran. on Graphics (SIGGRAPH) 30, 4. Article 97.
28. Zwerger, K. 2012. Wood and Wood Joints: Building Traditions of Europe, Japan and China. Birkhaüser Verlag.