“Point registration via efficient convex relaxation”
Conference:
Type(s):
Title:
- Point registration via efficient convex relaxation
Session/Category Title: CORRESPONDENCE & MAPPING
Presenter(s)/Author(s):
Moderator(s):
Abstract:
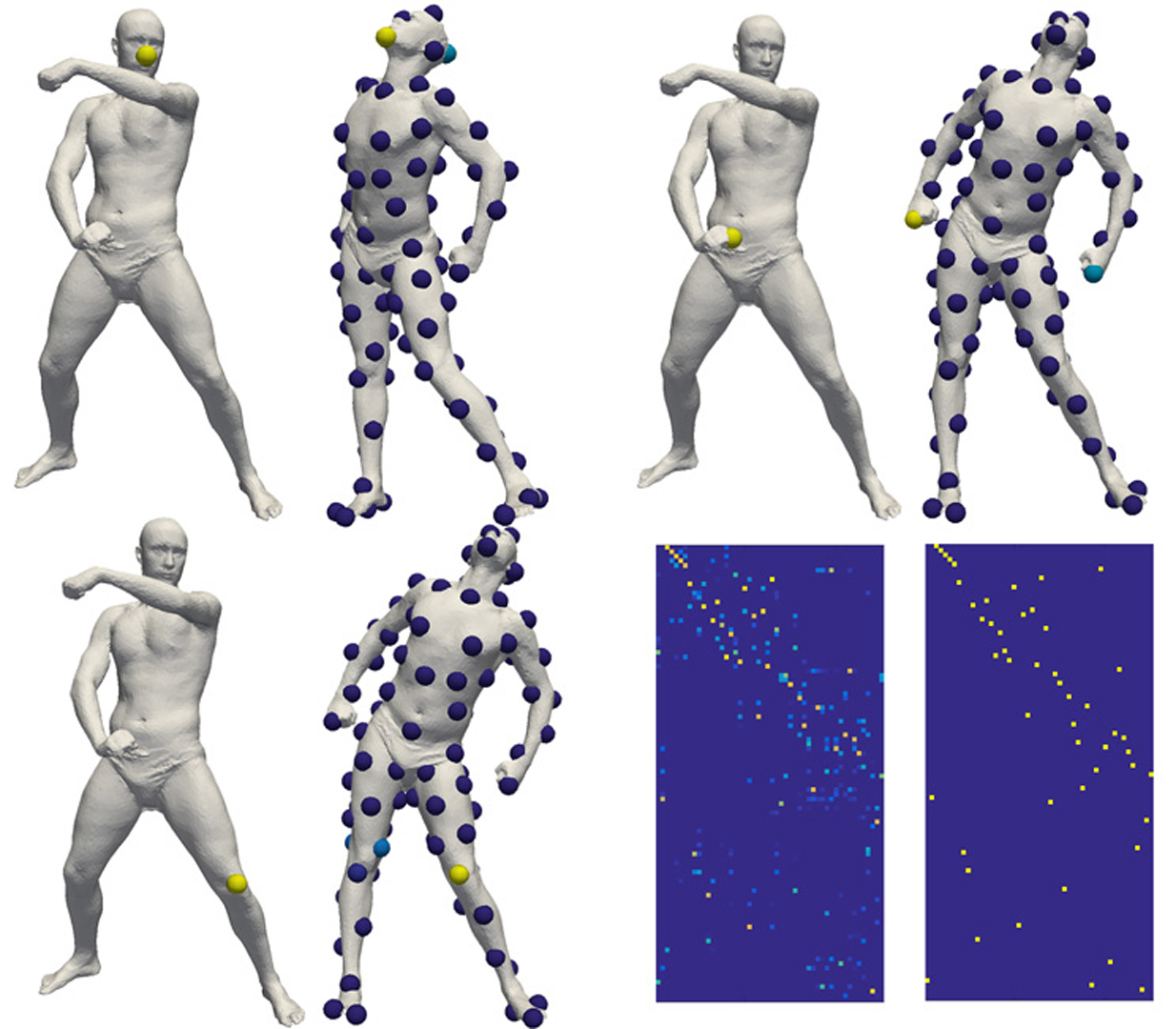
Point cloud registration is a fundamental task in computer graphics, and more specifically, in rigid and non-rigid shape matching. The rigid shape matching problem can be formulated as the problem of simultaneously aligning and labelling two point clouds in 3D so that they are as similar as possible. We name this problem the Procrustes matching (PM) problem. The non-rigid shape matching problem can be formulated as a higher dimensional PM problem using the functional maps method. High dimensional PM problems are difficult non-convex problems which currently can only be solved locally using iterative closest point (ICP) algorithms or similar methods. Good initialization is crucial for obtaining a good solution.We introduce a novel and efficient convex SDP (semidefinite programming) relaxation for the PM problem. The algorithm is guaranteed to return a correct global solution of the problem when matching two isometric shapes which are either asymmetric or bilaterally symmetric.We show our algorithm gives state of the art results on popular shape matching datasets. We also show that our algorithm gives state of the art results for anatomical classification of shapes. Finally we demonstrate the power of our method in aligning shape collections.
References:
1. Anguelov, D., Srinivasan, P., Koller, D., Thrun, S., Rodgers, J., and Davis, J. (2005). SCAPE: shape completion and animation of people. In ACM Transactions on Graphics (TOG), volume 24, pages 408–416. ACM. Google ScholarDigital Library
2. Aubry, M., Schlickewei, U., and Cremers, D. (2011). The wave kernel signature: A quantum mechanical approach to shape analysis. In Computer Vision Workshops (ICCV Workshops), 2011 IEEE International Conference on, pages 1626–1633. IEEE.Google ScholarCross Ref
3. Babai, L., Grigoryev, D. Y., and Mount, D. M. (1982). Isomorphism of graphs with bounded eigenvalue multiplicity. In Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing, STOC ’82, pages 310–324, New York, NY, USA. ACM. Google ScholarDigital Library
4. Belkin, M. and Niyogi, P. (2003). Laplacian eigenmaps for dimensionality reduction and data representation. Neural computation, 15(6):1373–1396. Google ScholarDigital Library
5. Berg, A. C., Berg, T. L., and Malik, J. (2005). Shape matching and object recognition using low distortion correspondences. In Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on, volume 1, pages 26–33. IEEE. Google ScholarDigital Library
6. Besl, P. and McKay, N. (1992). A method for registration of 3d shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(2):239–256. Google ScholarDigital Library
7. Bogo, F., Romero, J., Loper, M., and Black, M. J. (2014). FAUST: Dataset and evaluation for 3D mesh registration. In Computer Vision and Pattern Recognition (CVPR), 2014 IEEE Conference on, pages 3794–3801. IEEE. Google ScholarDigital Library
8. Boyer, D. M., Lipman, Y., Clair, E. S., Puente, J., Patel, B. A., Funkhouser, T., Jernvall, J., and Daubechies, I. (2011). Algorithms to automatically quantify the geometric similarity of anatomical surfaces. Proceedings of the National Academy of Sciences, 108(45):18221–18226.Google ScholarCross Ref
9. Bronstein, A. M., Bronstein, M. M., and Kimmel, R. (2006). Generalized multidimensional scaling: A framework for isometry-invariant partial surface matching. Proceedings of the National Academy of Sciences of the United States of America, 103(5):1168–1172.Google ScholarCross Ref
10. Brown, B. J. and Rusinkiewicz, S. (2007). Global non-rigid alignment of 3-d scans. ACM Transactions on Graphics (TOG), 26(3):21. Google ScholarDigital Library
11. Chen, Q. and Koltun, V. (2015). Robust nonrigid registration by convex optimization. In Proceedings of the IEEE International Conference on Computer Vision, pages 2039–2047. Google ScholarDigital Library
12. Dym, N. and Lipman, Y. (2016). Exact recovery with symmetries for procrustes matching. Technical report.Google Scholar
13. Eldar, Y., Lindenbaum, M., Porat, M., and Zeevi, Y. Y. (1997). The farthest point strategy for progressive image sampling. Image Processing, IEEE Transactions on, 6(9):1305–1315. Google ScholarDigital Library
14. Fischler, M. A. and Bolles, R. C. (1981). Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6):381–395. Google ScholarDigital Library
15. Fukuda, M., Kojima, M., Murota, K., and Nakata, K. (2000). Exploiting sparsity in semidefinite programming via matrix completion I: General framework. SIAM J. on Optimization, 11(3):647–674. Google ScholarDigital Library
16. Gelfand, N., Mitra, N. J., Guibas, L. J., and Pottmann, H. (2005). Robust global registration. In Proceedings of the Third Eurographics Symposium on Geometry Processing, SGP ’05, Aire-la-Ville, Switzerland, Switzerland. Eurographics Association. Google ScholarDigital Library
17. Giorgi, D., Biasotti, S., and Paraboschi, L. (2007). Shape retrieval contest 2007: Watertight models track. SHREC competition, 8.Google Scholar
18. Gower, J. C. and Dijksterhuis, G. B. (2004). Procrustes problems, volume 3. Oxford University Press Oxford.Google ScholarCross Ref
19. Grone, R., Johnson, C. R., Sá, E. M., and Wolkowicz, H. (1984). Positive definite completions of partial Hermitian matrices. Linear algebra and its applications, 58:109–124.Google Scholar
20. Huang, Q., Wang, F., and Guibas, L. (2014). Functional map networks for analyzing and exploring large shape collections. ACM Trans. Graph., 33(4):36:1–36:11. Google ScholarDigital Library
21. Jain, V., Zhang, H., and Van Kaick, O. (2007). Non-Rigid Spectral Correspondence of Triangle Meshes. International Journal of Shape Modeling, 13:101–124.Google ScholarCross Ref
22. Kendall, D. G. (1984). Shape manifolds, Procrustean metrics, and complex projective spaces. Bulletin of the London Mathematical Society, 16(2):81–121.Google ScholarCross Ref
23. Kezurer, I., Kovalsky, S. Z., Basri, R., and Lipman, Y. (2015). Tight relaxation of quadratic matching. Computer Graphics Forum, 34(5):115–128.Google ScholarCross Ref
24. Kim, V. G., Lipman, Y., and Funkhouser, T. (2011). Blended intrinsic maps. ACM Transactions on Graphics, 30(4):1. Google ScholarDigital Library
25. Leordeanu, M. and Hebert, M. (2005). A spectral technique for correspondence problems using pairwise constraints. In Computer Vision, 2005. ICCV 2005. Tenth IEEE International Conference on, volume 2, pages 1482–1489. IEEE. Google ScholarDigital Library
26. Li, H., Sumner, R. W., and Pauly, M. (2008). Global correspondence optimization for non-rigid registration of depth scans. In Computer Graphics Forum, volume 27, pages 1421–1430. Wiley Online Library. Google ScholarDigital Library
27. Lipman, Y. and Funkhouser, T. (2009). Möbius voting for surface correspondence. In ACM Transactions on Graphics (TOG), volume 28, page 72. ACM. Google ScholarDigital Library
28. Luo, Z.-Q., Ma, W.-k., So, A. M.-C., Ye, Y., and Zhang, S. (2010). Semidefinite relaxation of quadratic optimization problems. Signal Processing Magazine, IEEE, 27(3):20–34.Google ScholarCross Ref
29. Mémoli, F. and Sapiro, G. (2004). Comparing point clouds. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, SGP ’04, pages 32–40, New York, NY, USA. ACM. Google ScholarDigital Library
30. Mitteroecker, P. and Gunz, P. (2009). Advances in geometric mor-phometrics. Evolutionary Biology, 36(2):235–247.Google ScholarCross Ref
31. MOSEK (2015). The MOSEK optimization toolbox for MATLAB manual. Version 7.1 (Revision 49).Google Scholar
32. Nguyen, A., Ben-Chen, M., Welnicka, K., Ye, Y., and Guibas, L. (2011). An optimization approach to improving collections of shape maps. Computer Graphics Forum, 30(5):1481–1491.Google ScholarCross Ref
33. Ovsjanikov, M., Ben-Chen, M., Solomon, J., Butscher, A., and Guibas, L. (2012). Functional maps: a flexible representation of maps between shapes. ACM Transactions on Graphics (TOG), 31(4):30. Google ScholarDigital Library
34. Ovsjanikov, M., Mérigot, Q., Mémoli, F., and Guibas, L. (2010). One point isometric matching with the heat kernel. In Computer Graphics Forum, volume 29, pages 1555–1564. Wiley Online Library.Google ScholarCross Ref
35. Ovsjanikov, M., Sun, J., and Guibas, L. (2008). Global intrinsic symmetries of shapes. In Computer Graphics Forum, volume 27, pages 1341–1348. Wiley Online Library. Google ScholarDigital Library
36. Pinkall, U. and Polthier, K. (1993). Computing discrete minimal surfaces and their conjugates. Experimental mathematics, 2(1):15–36.Google Scholar
37. Pokrass, J., Bronstein, A. M., Bronstein, M. M., Sprechmann, P., and Sapiro, G. (2013). Sparse modeling of intrinsic correspondences. Computer Graphics Forum, 32(2 PART4):459–468.Google Scholar
38. Poljak, S., Rendl, F., and Wolkowicz, H. (1995). A recipe for semidefinite relaxation for (0, 1)-quadratic programming. Journal of Global Optimization, 7(1):51–73.Google ScholarCross Ref
39. Rusinkiewicz, S. and Levoy, M. (2001). Efficient variants of the ICP algorithm. Proceedings Third International Conference on 3-D Digital Imaging and Modeling, pages 145–152.Google ScholarCross Ref
40. Rustamov, R. M. (2007). Laplace-Beltrami eigenfunctions for deformation invariant shape representation. In Proceedings of the Fifth Eurographics Symposium on Geometry Processing, SGP ’07, pages 225–233, Aire-la-Ville, Switzerland, Switzerland. Eurographics Association. Google ScholarDigital Library
41. Saunderson, J., Parrilo, P. A., and Willsky, A. S. (2014). Semidefinite descriptions of the convex hull of rotation matrices. arXiv preprint arXiv:1403.4914.Google Scholar
42. Singer, A. and Wu, H.-T. (2012). Vector diffusion maps and the connection laplacian. Communications on Pure and Applied Mathematics, 65(8):1067–1144.Google ScholarCross Ref
43. Tam, G. K., Cheng, Z.-Q., Lai, Y.-K., Langbein, F. C., Liu, Y., Marshall, D., Martin, R. R., Sun, X.-F., and Rosin, P. L. (2013). Registration of 3D point clouds and meshes: a survey from rigid to nonrigid. Visualization and Computer Graphics, IEEE Transactions on, 19(7):1199–1217. Google ScholarDigital Library
44. Tevs, A., Bokeloh, M., Wand, M., Schilling, A., and Seidel, H.-P. (2009). Isometric registration of ambiguous and partial data. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on, pages 1185–1192. IEEE.Google Scholar
45. Van Kaick, O., Zhang, H., Hamarneh, G., and Cohen-Or, D. (2011). A survey on shape correspondence. In Computer Graphics Forum, volume 30, pages 1681–1707. Wiley Online Library.Google ScholarCross Ref
46. Waki, H., Kim, S., Kojima, M., and Muramatsu, M. (2006). Sums of squares and semidefinite programming relaxations for polynomial optimization problems with structured sparsity. SIAM Journal on Optimization, 17:218–242. Google ScholarDigital Library
47. Wand, M., Chang, W., Li, H., Mitra, N., Pauly, M., and Rusinkiewicz, S. (2011). Computing correspondences in geometric data sets tutorial. http://resources.mpi-inf.mpg.de/deformableShapeMatching/EG2011_Tutorial/.Google Scholar
48. Wei, L., Huang, Q., Ceylan, D., Vouga, E., and Li, H. (2015). Dense Human Body Correspondences Using Convolutional Networks.Google Scholar
49. Yang, J., Li, H., and Jia, Y. (2013). Go-ICP: Solving 3D Registration Efficiently and Globally Optimally. 2013 IEEE International Conference on Computer Vision, pages 1457–1464. Google ScholarDigital Library
50. Zeng, Y., Wang, C., Wang, Y., Gu, X., Samaras, D., and Paragios, N. (2010). Dense non-rigid surface registration using high-order graph matching. In Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pages 382–389. IEEE.Google ScholarCross Ref
51. Zhao, Q., Karisch, S. E., Rendl, F., and Wolkowicz, H. (1998). Semidefinite programming relaxations for the quadratic assignment problem. Journal of Combinatorial Optimization, 2(1):71–109.Google ScholarCross Ref
52. Zuffi, S. and Black, M. J. (2015). The stitched puppet: A graphical model of 3D human shape and pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3537–3546.Google ScholarCross Ref