“Neural Control Variates With Automatic Integration”
Conference:
Type(s):
Title:
- Neural Control Variates With Automatic Integration
Presenter(s)/Author(s):
Abstract:
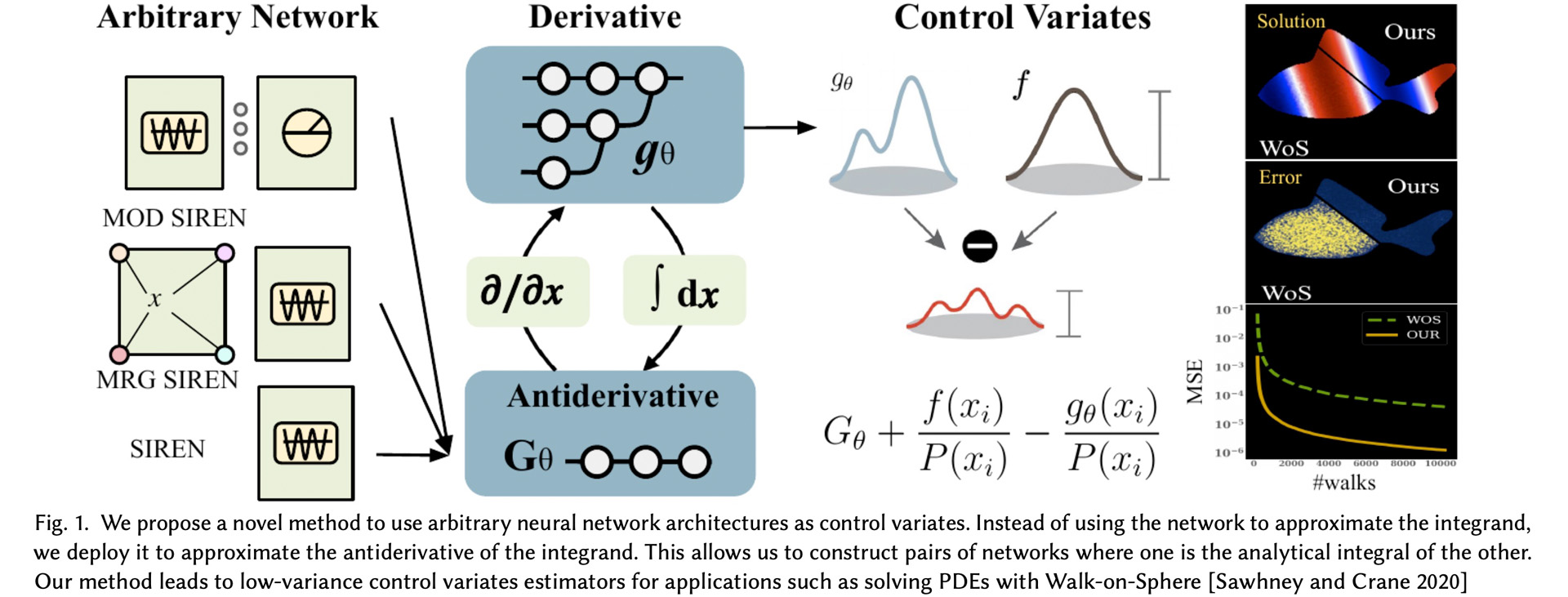
We present a method that uses arbitrary neural network architectures as control variates with automatic differentiation to improve Monte Carlo methods. Our approach creates unbiased, low-variance, and numerically stable Monte Carlo estimators for various problem setups. We demonstrate our method’s advantages in solving Laplace and Poisson equations using Walk-on-Sphere.
References:
[1]
Ghada Bakbouk and Pieter Peers. 2023. Mean Value Caching for Walk on Spheres. Eurographics (2023).
[2]
Ricky TQ Chen, Yulia Rubanova, Jesse Bettencourt, and David K Duvenaud. 2018. Neural ordinary differential equations. Advances in neural information processing systems 31 (2018), 1?9.
[3]
Petrik Clarberg and Tomas Akenine-M?ller. 2008. Exploiting visibility correlation in direct illumination. In Computer Graphics Forum, Vol. 27. Wiley Online Library, 1125?1136.
[4]
Keenan Crane, Ulrich Pinkall, and Peter Schr?der. 2013. Robust fairing via conformal curvature flow. ACM Transactions on Graphics (TOG) 32, 4 (2013), 1?10.
[5]
Laurent Dinh, David Krueger, and Yoshua Bengio. 2014. Nice: Non-linear independent components estimation, In International Conference on Learning Representations. International Conference on Learning Representations.
[6]
Laurent Dinh, Jascha Sohl-Dickstein, and Samy Bengio. 2016. Density estimation using Real NVP. In International Conference on Learning Representations.
[7]
Zineb El Filali Ech-Chafiq, J?r?me Lelong, and Adil Reghai. 2021. Automatic control variates for option pricing using neural networks. Monte Carlo Methods and Applications 27 (2021), 91 ? 104. https://api.semanticscholar.org/CorpusID:234204906
[8]
Tomas Geffner and Justin Domke. 2018. Using large ensembles of control variates for variational inference. Advances in Neural Information Processing Systems 31 (2018).
[9]
Peter W Glynn and Roberto Szechtman. 2002. Some new perspectives on the method of control variates. In Monte Carlo and Quasi-Monte Carlo Methods 2000: Proceedings of a Conference held at Hong Kong Baptist University, Hong Kong SAR, China, November 27?December 1, 2000. Springer, 27?49.
[10]
Qingqin Hua, Pascal Grittmann, and Philipp Slusallek. 2023. Revisiting controlled mixture sampling for rendering applications. ACM Transactions on Graphics (TOG) 42, 4 (2023), 1?13.
[11]
Diederik P. Kingma and Jimmy Ba. 2014. Adam: A Method for Stochastic Optimization. International Conference on Learning Representations abs/1412.6980 (2014). https://api.semanticscholar.org/CorpusID:6628106
[12]
Felix Kn?ppel, Keenan Crane, Ulrich Pinkall, and Peter Schr?der. 2015. Stripe Patterns on Surfaces. ACM Trans. Graph. 34 (2015). Issue 4.
[13]
Peter Kutz, Ralf Habel, Yining Karl Li, and Jan Nov?k. 2017. Spectral and decomposition tracking for rendering heterogeneous volumes. ACM Transactions on Graphics (TOG) 36, 4 (2017), 1?16.
[14]
Eric P Lafortune and Yves D Willems. 1994. Using the modified phong reflectance model for physically based rendering. Katholieke Universiteit Leuven. Departement Computerwetenschappen.
[15]
Zilu Li, Guandao Yang, Xi Deng, Christopher De Sa, Bharath Hariharan, and Steve Marschner. 2023. Neural Caches for Monte Carlo Partial Differential Equation Solvers. In SIGGRAPH Asia 2023 Conference Papers(SA ?23). Association for Computing Machinery, New York, NY, USA, Article 34, 10 pages. https://doi.org/10.1145/3610548.3618141
[16]
David B Lindell, Julien NP Martel, and Gordon Wetzstein. 2021. Autoint: Automatic integration for fast neural volume rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 14556?14565.
[17]
Wing Wah Loh. 1995. On the method of control variates. Stanford University.
[18]
Daniel Ma?tre and Roi Santos-Mateos. 2023. Multi-variable integration with a neural network. Journal of High Energy Physics 2023, 3 (2023), 1?16.
[19]
Ishit Mehta, Micha?l Gharbi, Connelly Barnes, Eli Shechtman, Ravi Ramamoorthi, and Manmohan Chandraker. 2021. Modulated periodic activations for generalizable local functional representations. In Proceedings of the IEEE/CVF International Conference on Computer Vision. 14214?14223.
[20]
Bailey Miller, Rohan Sawhney, Keenan Crane, and Ioannis Gkioulekas. 2023. Boundary Value Caching for Walk on Spheres. ACM Trans. Graph. 42, 4, Article 82 (jul 2023), 11 pages. https://doi.org/10.1145/3592400
[21]
Thomas M?ller, Alex Evans, Christoph Schied, and Alexander Keller. 2022. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. ACM Trans. Graph. 41, 4, Article 102 (July 2022), 15 pages. https://doi.org/10.1145/3528223.3530127
[22]
Thomas M?ller, Fabrice Rousselle, Alexander Keller, and Jan Nov?k. 2020. Neural control variates. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1?19.
[23]
Baptiste Nicolet, Fabrice Rousselle, Jan Novak, Alexander Keller, Wenzel Jakob, and Thomas M?ller. 2023. Recursive control variates for inverse rendering. ACM Transactions on Graphics (TOG) 42, 4 (2023), 1?13.
[24]
Arthur C Norman and PMA Moore. 1977. Implementing the new Risch integration algorithm. In Proceedings of the 4th International Colloquium on Advanced Computing Methods in Theoretical Physics. 99?110.
[25]
Ntumba Elie Nsampi, Adarsh Djeacoumar, Hans-Peter Seidel, Tobias Ritschel, and Thomas Leimk?hler. 2023. Neural Field Convolutions by Repeated Differentiation. ACM Transactions on Graphics (TOG) 42, 6 (2023), 1?11.
[26]
Anthony Pajot, Lo?c Barthe, and Mathias Paulin. 2014. Globally Adaptive Control Variate for Robust Numerical Integration. SIAM Journal on Scientific Computing 36, 4 (2014), A1708?A1730.
[27]
Armenak Petrosyan, Anton Dereventsov, and Clayton G Webster. 2020. Neural network integral representations with the ReLU activation function. In Mathematical and Scientific Machine Learning. PMLR, 128?143.
[28]
Yang Qi, Dario Seyb, Benedikt Bitterli, and Wojciech Jarosz. 2022. A bidirectional formulation for Walk on Spheres. In Computer Graphics Forum, Vol. 41. Wiley Online Library, 51?62.
[29]
Damien Rioux-Lavoie, Ryusuke Sugimoto, T?may ?zdemir, Naoharu H Shimada, Christopher Batty, Derek Nowrouzezahrai, and Toshiya Hachisuka. 2022. A Monte Carlo Method for Fluid Simulation. ACM Trans. Graph. 41, 6 (Nov. 2022), 1?16.
[30]
Robert H. Risch. 1969. The problem of integration in finite terms. Trans. Amer. Math. Soc. 139 (1969), 167?189. https://api.semanticscholar.org/CorpusID:122648356
[31]
Fabrice Rousselle, Wojciech Jarosz, and Jan Nov?k. 2016. Image-space control variates for rendering. ACM Transactions on Graphics (TOG) 35, 6 (2016), 1?12.
[32]
Corentin Sala?n, Adrien Gruson, Binh-Son Hua, Toshiya Hachisuka, and Gurprit Singh. 2022. Regression-based Monte Carlo integration. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1?14.
[33]
Rohan Sawhney and Keenan Crane. 2020. Monte Carlo geometry processing. ACM Trans. Graph. 39, 4 (Aug. 2020).
[34]
Rohan Sawhney, Bailey Miller, Ioannis Gkioulekas, and Keenan Crane. 2023. Walk on Stars: A Grid-Free Monte Carlo Method for PDEs with Neumann Boundary Conditions. ACM Trans. Graph. 42, 4, Article 80 (jul 2023), 20 pages. https://doi.org/10.1145/3592398
[35]
Rohan Sawhney, Dario Seyb, Wojciech Jarosz, and Keenan Crane. 2022. Grid-free Monte Carlo for PDEs with spatially varying coefficients. ACM Trans. Graph. 41, 4, Article 53 (jul 2022), 17 pages. https://doi.org/10.1145/3528223.3530134
[36]
Vincent Sitzmann, Julien Martel, Alexander Bergman, David Lindell, and Gordon Wetzstein. 2020. Implicit neural representations with periodic activation functions. Advances in neural information processing systems 33 (2020), 7462?7473.
[37]
Kartic Subr. 2021. Q-NET: A Network for Low-dimensional Integrals of Neural Proxies. In Computer Graphics Forum, Vol. 40. Wiley Online Library, 61?71.
[38]
Esteban G Tabak and Cristina V Turner. 2013. A family of nonparametric density estimation algorithms. Communications on Pure and Applied Mathematics 66, 2 (2013), 145?164.
[39]
Eric Veach. 1998. Robust Monte Carlo methods for light transport simulation. Stanford University.
[40]
Ruosi Wan, Mingjun Zhong, Haoyi Xiong, and Zhanxing Zhu. 2020. Neural control variates for Monte Carlo variance reduction. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2019, W?rzburg, Germany, September 16?20, 2019, Proceedings, Part II. Springer, 533?547.
[41]
Zihao Zhou and Rose Yu. 2023. Automatic Integration for Fast and Interpretable Neural Point Processes. In Learning for Dynamics and Control Conference. PMLR, University of Pennsylvania, 573?585.