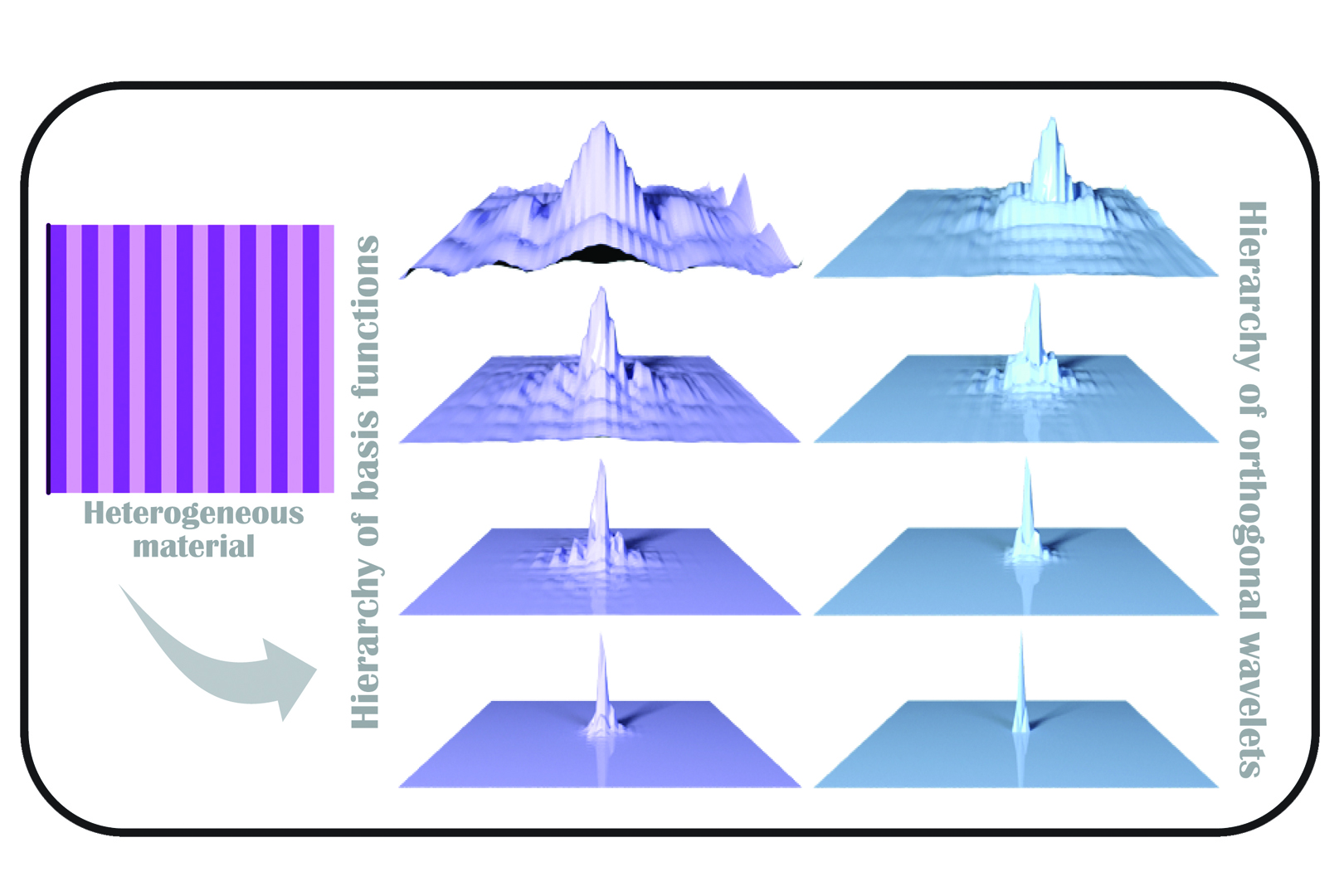
“Material-adapted refinable basis functions for elasticity simulation” by Chen, Budninskiy, Owhadi, Bao, Huang, et al. …
Conference:
Type(s):
Title:
- Material-adapted refinable basis functions for elasticity simulation
Session/Category Title:
- Accelerated Physics
Presenter(s)/Author(s):
Moderator(s):
Abstract:
In this paper, we introduce a hierarchical construction of material-adapted refinable basis functions and associated wavelets to offer efficient coarse-graining of linear elastic objects. While spectral methods rely on global basis functions to restrict the number of degrees of freedom, our basis functions are locally supported; yet, unlike typical polynomial basis functions, they are adapted to the material inhomogeneity of the elastic object to better capture its physical properties and behavior. In particular, they share spectral approximation properties with eigenfunctions, offering a good compromise between computational complexity and accuracy. Their construction involves only linear algebra and follows a fine-to-coarse approach, leading to a block-diagonalization of the stiffness matrix where each block corresponds to an intermediate scale space of the elastic object. Once this hierarchy has been precomputed, we can simulate an object at runtime on very coarse resolution grids and still capture the correct physical behavior, with orders of magnitude speedup compared to a fine simulation. We show on a variety of heterogeneous materials that our approach outperforms all previous coarse-graining methods for elasticity.
References:
1. Raymond Alcouffe, Achi Brandt, Joel Dendy, Jr., and James W. Painter. 1981. The Multi-Grid Method for the Diffusion Equation with Strongly Discontinuous Coefficients. SIAM J. Sci. Stat. Comput. 2, 4 (1981), 430–454.Google ScholarDigital Library
2. Ivo Babuška and John E. Osborn. 2000. Can a Finite Element Method Perform Arbitrarily Badly? Math. Comp. 69, 230 (2000), 443–462.Google ScholarDigital Library
3. Jernej Barbič and Doug L. James. 2005. Real-Time Subspace Integration for St. Venant-Kirchhoff Deformable Models. ACM Trans. Graph. 24, 3 (July 2005), 982–990.Google ScholarDigital Library
4. Jernej Barbič and Jovan Popović. 2008. Real-time Control of Physically Based Simulations Using Gentle Forces. In ACM SIGGRAPH Asia Proceedings. Article 163. Sofien Bouaziz, Sebastian Martin, Tiantian Liu, Ladislav Kavan, and Mark Pauly. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. ACM Trans. Graph. 33, 4, Article 154 (2014).Google Scholar
5. Achi Brandt, James Brannick, Karsten Kahl, and Irene Livshits. 2011. Bootstrap AMG. SIAM J. Scientific Computing 33, 2 (2011), 612–632.Google ScholarDigital Library
6. Christopher Brandt, Elmar Eisemann, and Klaus Hildebrandt. 2018. Hyper-reduced projective dynamics. ACM Transactions on Graphics (TOG) 37, 4 (2018), 80.Google ScholarDigital Library
7. Christopher Brandt and Klaus Hildebrandt. 2017. Compressed vibration modes of elastic bodies. Computer Aided Geometric Design 52–53 (2017), 297–312.Google Scholar
8. Mary E. Brewster and Gregory Beylkin. 1995. A Multiresolution Strategy for Numerical Homogenization. Applied and Computational Harmonic Analysis 2, 4 (1995), 327–349.Google ScholarCross Ref
9. Max Budninskiy, Houman Owhadi, and Mathieu Desbrun. 2019. Operator-adapted wavelets for finite-element differential forms. J. Comp. Phys. 388 (2019), 144–177.Google ScholarCross Ref
10. Desai Chen, David IW Levin, Wojciech Matusik, and Danny M Kaufman. 2017. Dynamics-aware numerical coarsening for fabrication design. ACM Trans. Graph. 36, 4, Article 84 (2017).Google ScholarDigital Library
11. Desai Chen, David IW Levin, Shinjiro Sueda, and Wojciech Matusik. 2015. Data-driven finite elements for geometry and material design. ACM Trans. Graph. 34, 4, Article 74 (2015).Google ScholarDigital Library
12. Jiong Chen, Hujun Bao, Tianyu Wang, Mathieu Desbrun, and Jin Huang. 2018. Numerical Coarsening Using Discontinuous Shape Functions. ACM Trans. Graph. 37, 4 (July 2018), Art. 120.Google ScholarDigital Library
13. Yuju Chen, David I. W. Levin, Danny Kaufmann, Uri Ascher, and Dinesh K. Pai. 2019. EigenFit for Consistent Elastodynamic Simulation Across Mesh Resolution. In Symp. Comp. Anim. Art. 5.Google Scholar
14. Min Gyu Choi and Hyeong-Seok Ko. 2005. Modal warping: real-time simulation of large rotational deformation and manipulation. IEEE Trans. Vis. Comp. Graph. 11, 1 (2005), 91–101.Google ScholarDigital Library
15. Timothy A. Davis. 2009. CHOLMOD: a sparse Cholesky factorization and modification package. http://faculty.cse.tamu.edu/davis/suitesparse.html.Google Scholar
16. Tyler De Witt, Christian Lessig, and Eugene Fiume. 2012. Fluid Simulation Using Laplacian Eigenfunctions. ACM Trans. Graph. 31, 1 (2012), Art. 10.Google Scholar
17. Gilles Debunne, Mathieu Desbrun, Marie-Paule Cani, and Alan H. Barr. 2001. Dynamic Real-time Deformations Using Space & Time Adaptive Sampling. In ACM SIGGRAPH Proceedings. 31–36.Google Scholar
18. Christian Dick, Joachim Georgii, and Ruediger Westermann. 2011. A Hexahedral Multigrid Approach for Simulating Cuts in Deformable Objects. IEEE Trans. Vis. Comp. Graph. 17, 11 (2011), 1663–1675.Google ScholarDigital Library
19. Mihai Dorobantu and Bjorn Engquist. 1998. Wavelet-Based Numerical Homogenization. SIAM J. Numer. Anal. 35, 2 (1998), 540–559.Google ScholarDigital Library
20. Joachim Georgii and Rüdiger Westermann. 2008. Corotated Finite Elements Made Fast and Stable. In Workshop in Virtual Reality Interactions and Physical Simulation.Google Scholar
21. Eitan Grinspun, Petr Krysl, and Peter Schröder. 2002. CHARMS: A Simple Framework for Adaptive Simulation. ACM Trans. Graph. 21, 3 (2002), 281–290.Google ScholarDigital Library
22. Robert L. Harder and Robert N. Desmarais. 1972. Interpolation using surface splines. J. Aircraft 9 (1972), 189–191.Google ScholarCross Ref
23. Kris K. Hauser, Chen Shen, and James F. O’Brien. 2003. Interactive Deformation Using Modal Analysis with Constraints. Graphics Interface (2003), 247–256.Google Scholar
24. Michael Hauth and Wolfgang Strasser. 2004. Corotational simulation of deformable solids. Journal of WSCG 12, 1–3 (2004), 1–8.Google Scholar
25. Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, and Konrad Polthier. 2012. Interactive Spacetime Control of Deformable Objects. ACM Trans. Graph. 31, 4, Article 71 (2012).Google ScholarDigital Library
26. Jin Huang, Xiaohan Shi, Xinguo Liu, Kun Zhou, Baining Guo, and Hujun Bao. 2006. Geometrically based potential energy for simulating deformable objects. The Visual Computer 22, 9 (2006), 740–748.Google ScholarDigital Library
27. Jin Huang, Yiying Tong, Kun Zhou, Hujun Bao, and Mathieu Desbrun. 2011. Interactive Shape Interpolation Through Controllable Dynamic Deformation. IEEE Trans. Vis. Comp. Graph. 17, 7 (2011), 983–992.Google ScholarDigital Library
28. Geoffrey Irving, Joseph Teran, and Ron Fedkiw. 2006. Tetrahedral and hexahedral invertible finite elements. Graphical Models 68, 2 (2006), 66–89.Google ScholarDigital Library
29. Inyong Jeon, Kwang-Jin Choi, Tae-Yong Kim, Bong-Ouk Choi, and Hyeong-Seok Ko. 2013. Constrainable multigrid for cloth. Comp. Graph. Forum 32, 7 (2013), 31–39.Google ScholarCross Ref
30. Lily Kharevych, Patrick Mullen, Houman Owhadi, and Mathieu Desbrun. 2009. Numerical coarsening of inhomogeneous elastic materials. ACM Trans. Graph. 28, 3, Article 51 (2009).Google ScholarDigital Library
31. Theodore Kim, Nils Thürey, Doug James, and Markus Gross. 2008. Wavelet Turbulence for Fluid Simulation. In ACM SIGGRAPH Proceedings. Article 50.Google Scholar
32. Marin Kobilarov, Keenan Crane, and Mathieu Desbrun. 2009. Lie Group Integrators for Animation and Control of Vehicles. ACM Trans. Graph. 28, 2, Article 16 (2009).Google ScholarDigital Library
33. Peter. Krysl, Sanjay Lall, and Jerrold E. Marsden. 2001. Dimensional model reduction in non-linear finite element dynamics of solids and structures. Int. J. Num. Methods Eng. 51, 4 (2001), 479–504.Google ScholarCross Ref
34. Tassilo Kugelstadt, Dan Koschier, and Jan Bender. 2018. Fast Corotated FEM using Operator Splitting. Comp. Graph. Forum 37, 8 (2018), 149–160.Google ScholarCross Ref
35. Siwang Li, Jin Huang, Fernando de Goes, Xiaogang Jin, Hujun Bao, and Mathieu Desbrun. 2014. Space-time Editing of Elastic Motion Through Material Optimization and Reduction. ACM Trans. Graph. 33, 4, Article 108 (2014).Google ScholarDigital Library
36. Beibei Liu, Gemma Mason, Julian Hodgson, Yiying Tong, and Mathieu Desbrun. 2015. Model-reduced Variational Fluid Simulation. ACM Trans. Graph. 34, 6, Article 244 (2015).Google ScholarDigital Library
37. Hsueh-Ti Derek Liu, Alec Jacobson, and Maks Ovsjanikov. 2019. Spectral Coarsening of Geometric Operators. ACM Trans. Graph. 38, 4, Article 105 (July 2019), 13 pages. Google ScholarDigital Library
38. Stéphane Mallat. 2008. A Wavelet Tour of Signal Processing: the Sparse Way. Academic Press.Google Scholar
39. Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-based elastic materials. ACM Trans. Graph. 30, 4, Article 72 (2011).Google ScholarDigital Library
40. Aleka McAdams, Yongning Zhu, Andrew Selle, Mark Empey, Rasmus Tamstorf, Joseph Teran, and Eftychios Sifakis. 2011. Efficient elasticity for character skinning with contact and collisions. ACM Trans. Graph. 30, 4 (2011), 37.Google ScholarDigital Library
41. Charles A. Micchelli and Theodore J. Rivlin. 1977. A survey of optimal recovery. In Optimal Estimation in Approximation Theory. 1–54.Google Scholar
42. Matthias Müller, Julie Dorsey, Leonard McMillan, Robert Jagnow, and Barbara Cutler. 2002. Stable Real-time Deformations. In Symp. Comp. Anim. 49–54.Google Scholar
43. Rahul Narain, Armin Samii, and James F. O’Brien. 2012. Adaptive Anisotropic Remeshing for Cloth Simulation. ACM Trans. Graph. 31, 6, Article 152 (2012).Google ScholarDigital Library
44. Matthieu Nesme, Paul G Kry, Lenka Jeřábková, and François Faure. 2009. Preserving topology and elasticity for embedded deformable models. ACM Trans. Graph. 28, 3, Article 52 (2009).Google ScholarDigital Library
45. Houman Owhadi. 2017. Multigrid with rough coefficients and multiresolution operator decomposition from hierarchical information games. SIAM Rev. 59, 1 (2017), 99–149.Google ScholarDigital Library
46. Houman Owhadi and Lei Zhang. 2017. Gamblets for opening the complexity-bottleneck of implicit schemes for hyperbolic and parabolic ODEs/PDEs with rough coefficients. J. Comp. Phys. 347 (2017), 99–128.Google ScholarCross Ref
47. Zherong Pan, Hujun Bao, and Jin Huang. 2015. Subspace dynamic simulation using rotation-strain coordinates. ACM Trans. Graph. 34, 6, Article 242 (2015).Google ScholarDigital Library
48. Julian Panetta, Qingnan Zhou, Luigi Malomo, Nico Pietroni, Paolo Cignoni, and Denis Zorin. 2015. Elastic Textures for Additive Fabrication. ACM Trans. Graph. 34, 4, Article 135 (2015).Google ScholarDigital Library
49. Alex Pentland and John Williams. 1989. Good Vibrations: Modal Dynamics for Graphics and Animation. SIGGRAPH Comput. Graph. 23, 3 (1989), 207–214.Google ScholarDigital Library
50. Christian Schumacher, Bernd Bickel, Jan Rys, Steve Marschner, Chiara Daraio, and Markus Gross. 2015. Microstructures to control elasticity in 3D printing. ACM Trans. Graph. 34, 4, Article 136 (2015).Google ScholarDigital Library
51. Christian Schumacher, Steve Marschner, Markus Cross, and Bernhard Thomaszewski. 2018. Mechanical characterization of structured sheet materials. ACM Trans. Graph. 37, 4 (2018), 148.Google ScholarDigital Library
52. Eric J. Stollnitz, Tony D. Derose, and David H. Salesin. 1996. Wavelets for Computer Graphics: Theory and Applications. Morgan Kaufmann Publishers Inc.Google Scholar
53. Raghunathan Sudarshan. 2005. Operator-adapted Finite Element Wavelets: theory and applications to a posteriori error estimation and adaptive computational modeling. Ph.D. Dissertation. Department of Civil and Environmental Engineering, Massachusetts Institute of Technology.Google Scholar
54. Rasmus Tamstorf, Toby Jones, and Stephen F. McCormick. 2015. Smoothed aggregation multigrid for cloth simulation. ACM Trans Graph. 34, 6 (2015), Art. 245.Google ScholarDigital Library
55. Rosell Torres, Jose M. Espadero, Felipe A. Calvo, and Miguel A. Otaduy. 2014. Interactive Deformation of Heterogeneous Volume Data. Lecture Notes in Computer Science 8789 (2014).Google Scholar
56. Adrien Treuille, Andrew Lewis, and Zoran Popović. 2006. Model Reduction for Real-time Fluids. In ACM SIGGRAPH Proceedings. 826–834.Google Scholar
57. Panayot S. Vassilevski. 2010. General constrained energy minimization interpolation mappings for AMG. SIAM J. Sci. Comput. 32, 1 (2010), 1–13.Google ScholarDigital Library
58. Gregory H Wannier. 1937. The structure of electronic excitation levels in insulating crystals. Physical Review 52, 3 (1937), 191.Google ScholarCross Ref
59. Irad Yavneh. 2006. Why Multigrid Methods Are So Efficient. Computing in Science Engineering 8, 6 (2006), 12–22.Google ScholarDigital Library
60. Yongning Zhu, Eftychios Sifakis, Joseph Teran, and Achi Brandt. 2010. An efficient multigrid method for the simulation of high-resolution elastic solids. ACM Trans. Graph. 29, 2 (2010), 16.Google ScholarDigital Library