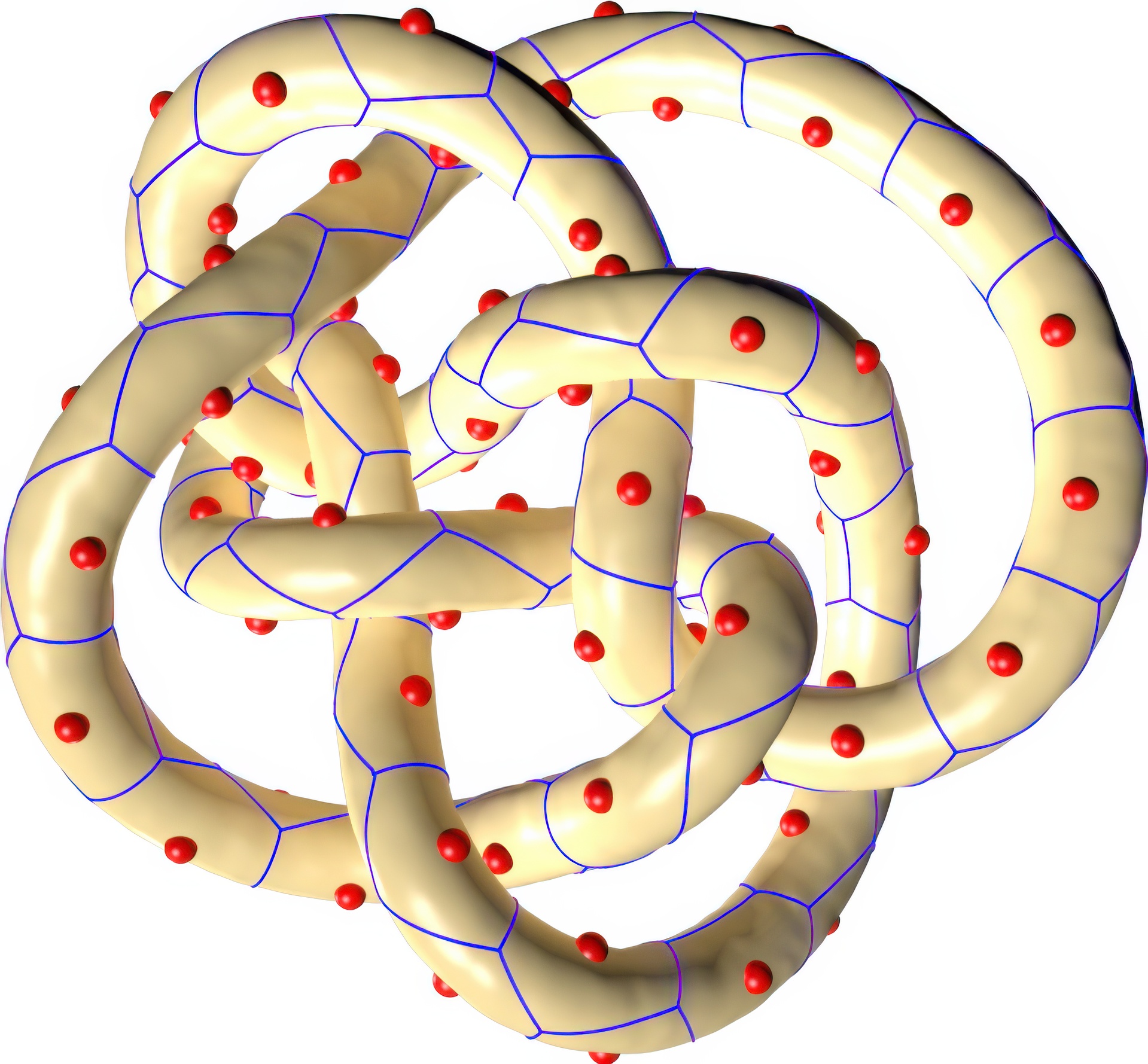
“Manifold differential evolution (MDE): a global optimization method for geodesic centroidal voronoi tessellations on meshes”
Conference:
Type(s):
Title:
- Manifold differential evolution (MDE): a global optimization method for geodesic centroidal voronoi tessellations on meshes
Session/Category Title:
- Tessellations
Presenter(s)/Author(s):
Abstract:
Computing centroidal Voronoi tessellations (CVT) has many applications in computer graphics. The existing methods, such as the Lloyd algorithm and the quasi-Newton solver, are efficient and easy to implement; however, they compute only the local optimal solutions due to the highly non-linear nature of the CVT energy. This paper presents a novel method, called manifold differential evolution (MDE), for computing globally optimal geodesic CVT energy on triangle meshes. Formulating the mutation operator using discrete geodesics, MDE naturally extends the powerful differential evolution framework from Euclidean spaces to manifold domains. Under mild assumptions, we show that MDE has a provable probabilistic convergence to the global optimum. Experiments on a wide range of 3D models show that MDE consistently out-performs the existing methods by producing results with lower energy. Thanks to its intrinsic and global nature, MDE is insensitive to initialization and mesh tessellation. Moreover, it is able to handle multiply-connected Voronoi cells, which are challenging to the existing geodesic CVT methods.
References:
1. Alliez, P., de Verdière, É. C., Devillers, O., and Isenburg, M. 2003. Isotropic surface remeshing. In Shape Modeling International, 49–58.
2. Alliez, P., de Verdière, É. C., Devillers, O., and Isenburg, M. 2005. Centroidal voronoi diagrams for isotropic surface remeshing. Graphical Models 67, 3, 204–231.
3. Berntsen, J., and Espelid, T. O. 1992. Algorithm 706: Dcutri: An algorithm for adaptive cubature over a collection of triangles. ACM Trans. Math. Softw. 18, 3, 329–342.
4. Boender, C. G. E., and Romeijn, H. E. 1995. Stochastic methods. In Handbook of Global Optimization, Kluwer Academic Publishers, 829–869.
5. Cheng, P., Miao, C., Liu, Y.-J., Tu, C., and He, Y. 2016. Solving the initial value problem of discrete geodesics. Computer-Aided Design 70, 144–152.
6. Crane, K., Weischedel, C., and Wardetzky, M. 2013. Geodesics in heat: A new approach to computing distance based on heat flow. ACM Trans. Graph. 32, 5, 152:1–152:11.
7. Das, S., and Suganthan, P. N. 2011. Differential evolution: A survey of the state-of-the-art. IEEE Transactions on Evolutionary Computation 15, 1, 4–31.
8. Das, S., Mullick, S. S., and Suganthan, P. N. 2016. Recent advances in differential evolution – an updated survey. Swarm and Evolutionary Computation 27, 1–30. Cross Ref
9. Du, Q., Faber, V., and Gunzburger, M. 1999. Centroidal Voronoi tessellations: Applications and algorithms. SIAM Review 41, 4, 637–676.
10. Du, Q., Gunzburger, M. D., and Ju, L. 2003. Constrained centroidal Voronoi tessellations for surfaces. SIAM Journal on Scientific Computing 24, 5, 1488–1506.
11. Engelbrecht, A. P. 2006. Fundamentals of Computational Swarm Intelligence. John Wiley & Sons.
12. Ghosh, S., Das, S., Vasilakos, A. V., and Suresh, K. 2012. On convergence of differential evolution over a class of continuous functions with unique global optimum. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics 42, 1, 107–124.
13. Horst, R., Pardalos, P. M., and Thoai, N. V. 2000. Introduction to Global Optimization. 2nd edition, Kluwer Academic Publishers.
14. Kimmel, R., and Sethian, J. 1998. Computing geodesic paths on manifolds. Proceedings of National Academy of Sciences 95, 8431–8435. Cross Ref
15. Korte, B., and Vygen, J. 2006. Combinatorial Optimization: Theory and Algorithms. 3rd edition, Springer-Verlag.
16. Leung, Y.-S., Wang, X., He, Y., Liu, Y.-J., and Wang, C. C. L. 2015. A unified framework for isotropic meshing based on narrow-banded euclidean distance transformation. Computational Visual Media 1, 3, 239–251. Cross Ref
17. Lévy, B., and Liu, Y. 2010. Lp centroidal voronoi tessellation and its applications. ACM Trans. Graph. 29, 4, 119:1–119:11.
18. Liu, Y., Wang, W., Lévy, B., Sun, F., Yan, D.-M., Lu, L., and Yang, C. 2009. On centroidal Voronoi tessellation – energy smoothness and fast computation. ACM Trans. Graph. 28, 4, 101:1–101:17.
19. Liu, Y.-J., Chen, Z., and Tang, K. 2011. Construction of iso-contours, bisectors, and Voronoi diagrams on triangulated surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence 33, 8, 1502–1517.
20. Liu, Y.-J. 2015. Semi-continuity of skeletons in 2-manifold and discrete voronoi approximation. IEEE Transactions on Pattern Analysis and Machine Intelligence 37, 9, 1938–1944. Cross Ref
21. Lloyd, S. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2, 129 — 137.
22. Lu, L., Sun, F., Pan, H., and Wang, W. 2012. Global optimization of centroidal Voronoi tessellation with monte carlo approach. IEEE Transactions on Visualization and Computer Graphics 18, 11, 1880–1890.
23. Mitchell, J. S., Mount, D. M., and Papadimitriou, C. H. 1987. The discrete geodesic problem. SIAM Journal on Computing 16, 4, 647–668.
24. Papoulis, A. 1991. Probability, Random Variables and Stochastic Processes. Third Edition, McGraw-Hill, Inc.
25. Price, K., Storn, R. M., and Lampinen, J. A. 2005. Differential Evolution: A Practical Approach to Global Optimization. Springer.
26. Qu, B., Liang, J., Wang, Z., Chen, Q., and Suganthan, P. 2016. Novel benchmark functions for continuous multimodal optimization with comparative results. Swarm and Evolutionary Computation 26, 23–34. Cross Ref
27. Rong, G., Jin, M., Shuai, L., and Guo, X. 2011. Centroidal voronoi tessellation in universal covering space of manifold surfaces. Comput. Aided Geom. Des. 28, 8, 475–496.
28. Rong, G., Liu, Y., Wang, W., Yin, X., Gu, X., and Guo, X. 2011. GPU-assisted computation of centroidal Voronoi tessellation. IEEE Transactions on Visualization and Computer Graphics 17, 3, 345–356.
29. Vesterstrom, J., and Thomsen, R. 2004. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proc. 6th Congress on Evolutionary Computation, 1980–1987.
30. Wandzurat, S., and Xiao, H. 2003. Symmetric quadrature rules on a triangle. Computers & Mathematics with Applications 45, 12, 1829–1840. Cross Ref
31. Wang, X., Ying, X., Liu, Y.-J., Xin, S.-Q., Wang, W., Gu, X., Mueller-Wittig, W., and He, Y. 2015. Intrinsic computation of centroidal Voronoi tessellation (cvt) on meshes. Computer-Aided Design 58, 51–61.
32. Xu, C., Wang, T. Y., Liu, Y., Liu, L., and He, Y. 2015. Fast wavefront propagation (FWP) for computing exact geodesic distances on meshes. IEEE Trans. Vis. Comput. Graph. 21, 7, 822–834.
33. Yan, D., and Wonka, P. 2016. Non-obtuse remeshing with centroidal Voronoi tessellation. IEEE Trans. Vis. Comput. Graph. 22, 9, 2136–2144. Cross Ref
34. Yan, D.-M., Lévy, B., Liu, Y., Sun, F., and Wang, W. 2009. Isotropic remeshing with fast and exact computation of restricted Voronoi diagram. Comput. Graph. Forum 28, 5, 1445–1454.
35. Yan, D., Bao, G., Zhang, X., and Wonka, P. 2014. Low-resolution remeshing using the localized restricted voronoi diagram. IEEE Trans. Vis. Comput. Graph. 20, 10, 1418–1427. Cross Ref
36. Ying, X., Wang, X., and He, Y. 2013. Saddle vertex graph (svg): A novel solution to the discrete geodesic problem. ACM Trans. Graph. 32, 6, 170:1–170:12.
37. Ying, X., Xin, S., and He, Y. 2014. Parallel Chen-Han (PCH) algorithm for discrete geodesics. ACM Trans. Graph. 33, 1, 9:1–9:11.
38. Zaharie, D. 2001. On the explorative power of differential evolution algorithms. In Proc. 3rd Int. Workshop Symbolic and Numerical Algorithms on Scientific Computing.