“Lp Centroidal Voronoi Tessellation and its applications” by Levy and Liu
Conference:
Type(s):
Title:
- Lp Centroidal Voronoi Tessellation and its applications
Presenter(s)/Author(s):
Abstract:
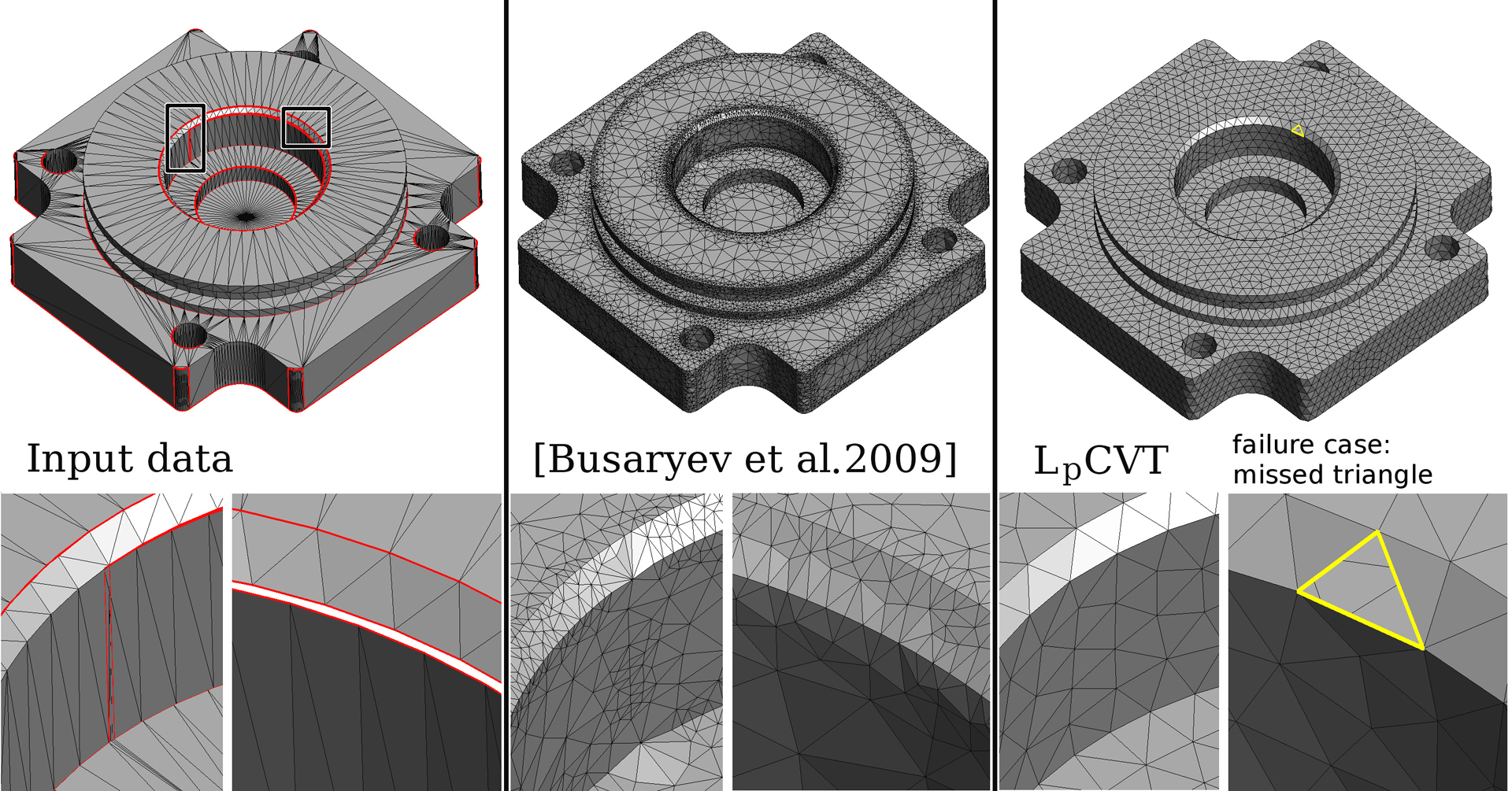
This paper introduces Lp-Centroidal Voronoi Tessellation (Lp-CVT), a generalization of CVT that minimizes a higher-order moment of the coordinates on the Voronoi cells. This generalization allows for aligning the axes of the Voronoi cells with a predefined background tensor field (anisotropy). Lp-CVT is computed by a quasi-Newton optimization framework, based on closed-form derivations of the objective function and its gradient. The derivations are given for both surface meshing (Ω is a triangulated mesh with per-facet anisotropy) and volume meshing (Ω is the interior of a closed triangulated mesh with a 3D anisotropy field). Applications to anisotropic, quad-dominant surface remeshing and to hexdominant volume meshing are presented. Unlike previous work, Lp-CVT captures sharp features and intersections without requiring any pre-tagging.
References:
1. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. ACM Transactions on Graphics 22, 3, 485–493. Google ScholarDigital Library
2. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. ACM Transactions on Graphics 24, 3, 617–625. Google ScholarDigital Library
3. Boissonnat, J.-D., and Oudot, S. 2006. Provably good sampling and meshing of Lipschitz surfaces. In SCG ’06: Proceedings of the twenty-second annual symposium on Computational geometry, 337–346. Google ScholarDigital Library
4. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixedinteger quadrangulation. ACM Transactions on Graphics 28, 3, 1–10. Google ScholarDigital Library
5. Busaryev, O., Dey, T. K., and Levine, J. A. 2009. Repairing and meshing imperfect shapes with Delaunay refinement. In SPM ’09: 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling, 25–33. Google ScholarDigital Library
6. Chen, L., and Xu, J. 2004. Optimal Delaunay triangulations. Journal of Computational Mathematics 22, 2, 299–308.Google Scholar
7. Cohen-Steiner, D., Alliez, P., and Desbrun, M. 2004. Variational shape approximation. ACM Transactions on Graphics 23, 905–914. Google ScholarDigital Library
8. Daniels-II, J., Silva, C. T., and Cohen, E. 2009. Localized quadrilateral coarsening. Computer Graphics Forum 28, 1437–1444.Google ScholarDigital Library
9. Dey, T. K., and Levine, J. A. 2008. Delaunay meshing of piecewise smooth complexes without expensive predicates. Algorithms 2, 1327–1349. OSU-CISRC-7/08-TR40.Google ScholarCross Ref
10. Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and Hart, J. C. 2006. Spectral surface quadrangulation. ACM Transactions on Graphics 25, 1057–1066. Google ScholarDigital Library
11. Du, Q., and Emelianenko, M. 2006. Acceleration schemes for computing centroidal Voronoi tessellations. Numerical Linear Algebra with Applications 13, 2–3, 173–192.Google ScholarCross Ref
12. Du, Q., and Wang, D. 2003. Tetrahedral mesh generation and optimization based on centroidal Voronoi tessellations. International Journal for Numerical Methods in Engineering 56, 1355–1373.Google ScholarCross Ref
13. Du, Q., and Wang, D. 2005. Anisotropic centroidal Voronoi tessellations and their applications. SIAM Journal on Scientific Computing 26, 3, 737–761. Google ScholarDigital Library
14. Du, Q., Faber, V., and Gunzburger, M. 1999. Centroidal Voronoi tessellations: applications and algorithms. SIAM Review 41, 4, 637–676. Google ScholarDigital Library
15. Edelsbrunner, H., and Shah, N. R. 1997. Triangulating topological spaces. International Journal of Computational Geometry & Applications 7, 4, 365–378.Google Scholar
16. Huang, J., Zhang, M., Ma, J., Liu, X., Kobbelt, L., and Bao, H. 2008. Spectral quadrangulation with orientation and alignment control. ACM Transactions on Graphics 27. Google ScholarDigital Library
17. Iri, M., Murota, K., and Ohya, T. 1984. A fast Voronoidiagram algorithm with applications to geographical optimization problems. In Proc. IFIP, 273–288.Google Scholar
18. Itoh, T., and Shimada, K. 2001. Automatic conversion of triangular meshes into quadrilateral meshes with directionality. International Journal of CAD/CAM.Google Scholar
19. Kalberer, F., Nieser, M., and Polthier, K. 2007. Quadcover — surface parameterization using branched coverings. Computer Graphics Forum 26, 375–384.Google ScholarCross Ref
20. Labelle, F., and Shewchuk, J. R. 2003. Anisotropic Voronoi diagrams and guaranteed-quality anisotropic mesh generation. In SCG ’03: Proceedings of the nineteenth annual symposium on Computational geometry, 191–200. Google ScholarDigital Library
21. Lai, Y.-K., Kobbelt, L., and Hu, S.-M. 2008. An incremental approach to feature aligned quad dominant remeshing. In ACM SPM conference proceedings. Google ScholarDigital Library
22. Lasserre, J., and Avrachenkov, K. 2001. Integration on a simplex: The multi-dimensional version of ∫a
b x
p dx. American Mathematics Monthly 108, 151–154.Google ScholarCross Ref
23. Liu, Y., Wang, W., Lévy, B., Sun, F., Yan, D.-M., Lu, L., and Yang, C. 2009. On centroidal Voronoi tessellation—energy smoothness and fast computation. ACM Transactions on Graphics 28, 4, 1–17. Google ScholarDigital Library
24. Lloyd, S. P. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2, 129–137.Google ScholarDigital Library
25. Maréchal, L. 2009. Advances in octree-based all-hexahedral mesh generation: handling sharp features. In 18th International Meshing Roundtable conference proceedings.Google ScholarCross Ref
26. Martin, T., Cohen, E., and Kirby, M. 2008. Volumetric parameterization and trivariate B-spline fitting using harmonic functions. In SPM ’08: Proceedings of the 2008 ACM symposium on Solid and physical modeling, 269–280. Google ScholarDigital Library
27. Meshkat, S., and Talmor, D. 2000. Generating a mixed mesh of hexahedra, pentahedra and tetrahedra from an underlying tetrahedral mesh. International Journal for Numerical Methods in Engineering 49, 17–30.Google ScholarCross Ref
28. Minka, T. 1997. Old and new matrix algebra useful for statistics. Tech. rep., MIT Media Lab. revised 12/00.Google Scholar
29. Mount, D. M., and Arya, S. 1997. ANN: A library for approximate nearest neighbor searching. In Proceedings CGC Workshop on Computational Geometry, 33–40.Google Scholar
30. Owen, S. J., and Saigal, S. 2000. H-Morph: An indirect approach to advancing front hex meshing. International Journal for Numerical Methods in Engineering 49, 289–312.Google ScholarCross Ref
31. Ray, N., Li, W. C., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Transactions on Graphics 25, 4, 1460–1485. Google ScholarDigital Library
32. Shepherd, J. F., and Johnson, C. R. 2008. Hexahedral mesh generation constraints. Engineering with Computers 24, 3, 195–213. Google ScholarDigital Library
33. Shepherd, J., Mitchell, S. A., Knupp, P., and White, D. 2000. Methods for multisweep automation. In 9th Intl. Meshing Roundtable conference proceedings.Google Scholar
34. Staten, M. L., Owen, S. J., and Blacker, T. D. 2005. Unconstrained paving and plastering: A new idea for all hexahedral mesh generation. In International Meshing Roundtable conference proceedings.Google Scholar
35. Steiner, D., and Fischer, A. 2005. Planar parameterization for closed manifold genus-g meshes using any type of positive weights. Journal of Computational Methods in Information Science and Engineering 5, 2.Google Scholar
36. Tchon, K.-F., and Camarero, R. 2006. Quad-dominant mesh adaptation using specialized simplicial optimization. In 15th International Meshing Roundtable conference proceedings.Google Scholar
37. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. In SGP ’06: Proceedings of the fourth Eurographics symposium on Geometry processing, 201–210. Google ScholarDigital Library
38. Tournois, J., Wormser, C., Alliez, P., and Desbrun, M. 2009. Interleaving delaunay refinement and optimization for practical isotropic tetrahedron mesh generation. ACM Transactions on Graphics 28, 75:1–75:9. Google ScholarDigital Library
39. Valette, S., Chassery, J.-M., and Prost, R. 2008. Generic remeshing of 3D triangular meshes with metric-dependent discrete Voronoi diagrams. IEEE Transactions on Visualization and Computer Graphics 14, 2, 369–381. Google ScholarDigital Library
40. Vyas, V., and Shimada, K. 2009. Tensor-guided hex-dominant mesh generation with targeted all-hex regions. In 18th International Meshing Roundtable conference proceedings.Google Scholar
41. Yamakawa, S., and Shimada, K. 2003. Anisotropic tetrahedral meshing via bubble packing and advancing front. International Journal for Numerical Methods in Engineering 57.Google Scholar
42. Yamakawa, S., and Shimada, K. 2003. Fully-automated hexdominant mesh generation with directionality control via packing rectangular solid cells. International Journal for Numerical Methods in Engineering 57, 2099–2129.Google ScholarCross Ref
43. Yan, D.-M., Lévy, B., Liu, Y., Sun, F., and Wang, W. 2009. Isotropic remeshing with fast and exact computation of restricted Voronoi diagram. Computer Graphics Forum 28, 5, 1445–1454.Google ScholarDigital Library