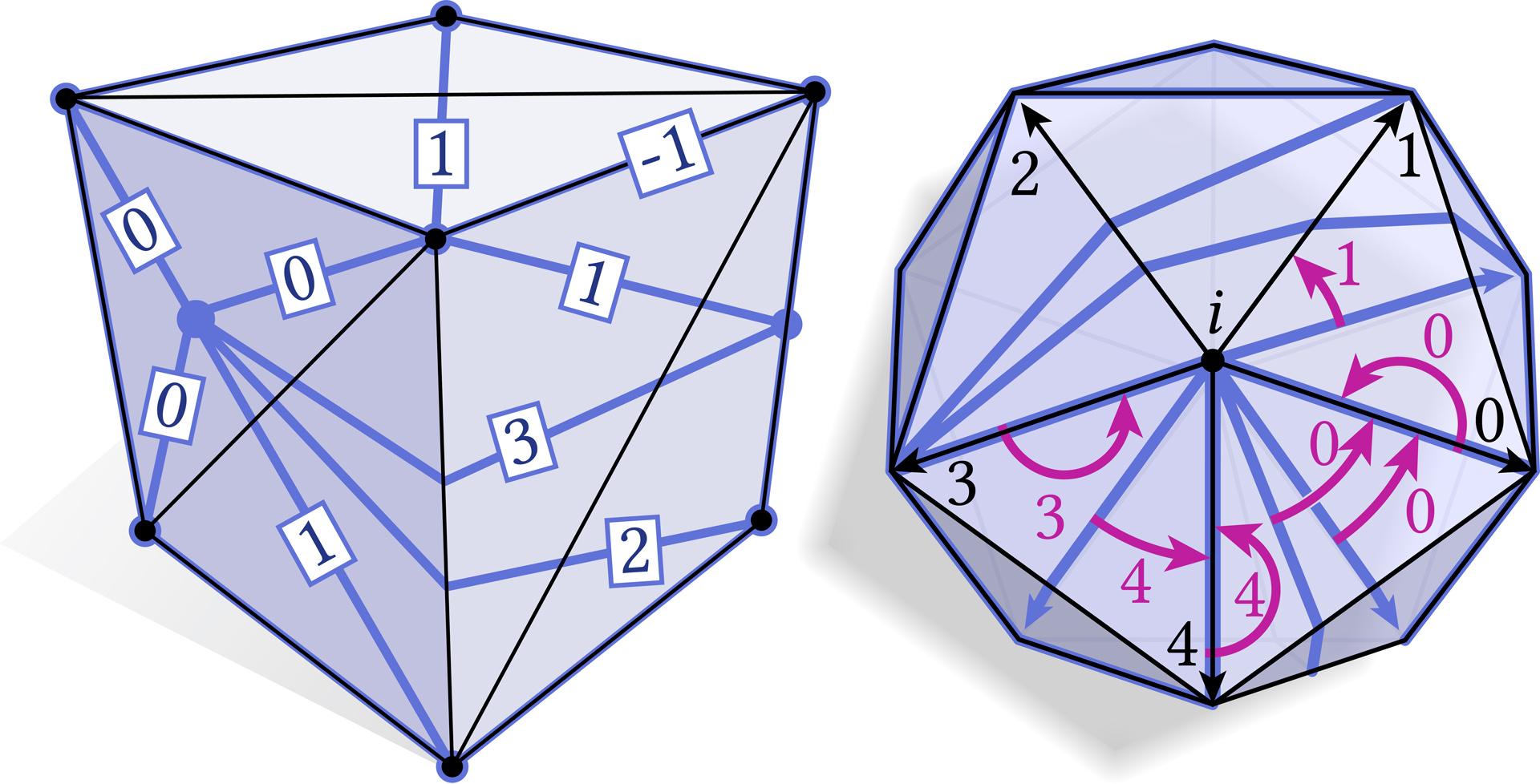
“Integer coordinates for intrinsic geometry processing” by Gillespie, Sharp and Crane
Conference:
Type(s):
Title:
- Integer coordinates for intrinsic geometry processing
Session/Category Title:
- Geometry Processing and Simulation
Presenter(s)/Author(s):
Abstract:
This paper describes a numerically robust data structure for encoding intrinsic triangulations of polyhedral surfaces. Many applications demand a correspondence between the intrinsic triangulation and the input surface, but existing data structures either rely on floating point values to encode correspondence, or do not support remeshing operations beyond basic edge flips. We instead provide an integer-based data structure that guarantees valid correspondence, even for meshes with near-degenerate elements. Our starting point is the framework of normal coordinates from geometric topology, which we extend to the broader set of operations needed for mesh processing (vertex insertion, edge splits, etc.). The resulting data structure can be used as a drop-in replacement for earlier schemes, automatically improving reliability across a wide variety of applications. As a stress test, we successfully compute an intrinsic Delaunay refinement and associated subdivision for all manifold meshes in the Thingi10k dataset. In turn, we can compute reliable and highly accurate solutions to partial differential equations even on extremely low-quality meshes.
References:
1. Mark Bell. 2013–2018. flipper (Computer Software). https://pypi.python.org/pypi/flipper.
2. Mark Bell. 2015. Recognising mapping classes. Ph.D. Dissertation. University of Warwick.
3. Alexander I Bobenko and Ivan Izmestiev. 2008. Alexandrov’s theorem, weighted Delaunay triangulations, and mixed volumes. In Annales de l’institut Fourier, Vol. 58. 447–505.
4. Alexander I Bobenko and Boris A Springborn. 2007. A discrete Laplace-Beltrami operator for simplicial surfaces. Discrete & Computational Geometry 38, 4 (2007), 740–756.
5. Mario Botsch, Leif Kobbelt, Mark Pauly, Pierre Alliez, and Bruno Lévy. 2010. Polygon Mesh Processing. CRC press.
6. L Paul Chew. 1993. Guaranteed-quality mesh generation for curved surfaces. In Proceedings of the ninth annual symposium on Computational geometry. 274–280.
7. Paolo Cignoni, Marco Callieri, Massimiliano Corsini, Matteo Dellepiane, Fabio Ganovelli, and Guido Ranzuglia. 2008. Meshlab: an open-source mesh processing tool.. In Eurographics Italian chapter conference, Vol. 2008. Salerno, Italy, 129–136.
8. Keenan Crane, Clarisse Weischedel, and Max Wardetzky. 2017. The Heat Method for Distance Computation. Commun. ACM 60, 11 (Oct. 2017), 90–99.
9. Olivier Devillers and Sylvain Pion. 2003. Efficient Exact Geometric Predicates for Delauny Triangulations.. In Proc. 5th Workshop Algorithm Eng. Exper. 37–44.
10. Ivan Dynnikov. 2020. Counting intersections of normal curves. arXiv preprint arXiv:2010.01638 (2020).
11. Jeff Erickson and Amir Nayyeri. 2013. Tracing compressed curves in triangulated surfaces. Discrete & Computational Geometry 49, 4 (2013), 823–863.
12. Benson Farb and Dan Margalit. 2011. A primer on mapping class groups. Princeton University Press.
13. Patrick E Farrell, Matthew D Piggott, Christopher C Pain, Gerard J Gorman, and Cian R Wilson. 2009. Conservative interpolation between unstructured meshes via supermesh construction. Computer methods in applied mechanics and engineering 198, 33-36 (2009), 2632–2642.
14. Matthew Fisher, Boris Springborn, Alexander I Bobenko, and Peter Schröder. 2006. An algorithm for the construction of intrinsic Delaunay triangulations with applications to digital geometry processing. In ACM SIGGRAPH 2006. 69–74.
15. Marco Fumero, Michael Möller, and Emanuele Rodolà. 2020. Nonlinear spectral geometry processing via the tv transform. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1–16.
16. Mark Gillespie, Boris Springborn, and Keenan Crane. 2021. Discrete Conformal Equivalence of Polyhedral Surfaces. ACM Trans. Graph. 40, 4 (2021).
17. Wolfgang Haken. 1961. Theorie Der Normalflächen: Ein Isotopiekriterium Für Den Kreisknoten. Acta Math. 105, 3-4 (1961).
18. Joel Hass and Maria Trnkova. 2020. Approximating Isosurfaces by Guaranteed-quality Triangular Meshes. Computer Graphics Forum (2020).
19. Allen Hatcher. 2002. Algebraic Topology. Cambridge University Press.
20. Yixin Hu, Teseo Schneider, Bolun Wang, Denis Zorin, and Daniele Panozzo. 2020. Fast tetrahedral meshing in the wild. ACM Transactions on Graphics (TOG) 39, 4 (2020), 117–1.
21. Yixin Hu, Qingnan Zhou, Xifeng Gao, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2018. Tetrahedral meshing in the wild. ACM Trans. Graph. 37, 4 (2018), 60–1.
22. Claude Indermitte, Th M Liebling, Marc Troyanov, and Heinz Clémençon. 2001. Voronoi diagrams on piecewise flat surfaces and an application to biological growth. Theoretical Computer Science 263, 1-2 (2001), 263–274.
23. Zhongshi Jiang, Teseo Schneider, Denis Zorin, and Daniele Panozzo. 2020. Bijective projection in a shell. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1–18.
24. Xiangmin Jiao and Michael T Heath. 2004. Common-refinement-based data transfer between non-matching meshes in multiphysics simulations. Internat. J. Numer. Methods Engrg. 61, 14 (2004), 2402–2427.
25. Hellmuth Kneser. 1929. Geschlossene Flächen in Dreidimensionalen Mannigfaltigkeiten. Jahresber. Dtsch. Math.-Ver. 38 (1929).
26. Felix Knöppel, Keenan Crane, Ulrich Pinkall, and Peter Schröder. 2013. Globally optimal direction fields. ACM Trans. Graph. 32, 4 (2013).
27. Dimas Martínez Morera, Paulo Cezar Carvalho, and Luiz Velho. 2008. Modeling on triangulations with geodesic curves. The Visual Computer 24, 12 (2008), 1025–1037.
28. Lee Mosher. 1988. Tiling the Projective Foliation Space of a Punctured Surface. Trans. Amer. Math. Soc. (1988).
29. Alexander Rand. 2011. Where and How Chew’s Second Delaunay Refinement Algorithm Works.. In CCCG.
30. Rohan Sawhney and Keenan Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 39, 4 (2020).
31. Marcus Schaefer, Eric Sedgwick, and Daniel Štefankovič. 2002. Algorithms for normal curves and surfaces. In International Computing and Combinatorics Conference. Springer, 370–380.
32. Marcus Schaefer, Eric Sedgwick, and Daniel Stefankovic. 2008. Computing Dehn Twists and Geometric Intersection Numbers in Polynomial Time.. In CCCG, Vol. 20. 111–114.
33. Max Schindler and Evan Chen. 2012. Barycentric Coordinates in Olympiad Geometry. Olympiad Articles (2012), 1–40.
34. Teseo Schneider, Yixin Hu, Jérémie Dumas, Xifeng Gao, Daniele Panozzo, and Denis Zorin. 2018. Decoupling simulation accuracy from mesh quality. ACM transactions on graphics (2018).
35. Silvia Sellán, Herng Yi Cheng, Yuming Ma, Mitchell Dembowski, and Alec Jacobson. 2019. Solid geometry processing on deconstructed domains. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 564–579.
36. Nicholas Sharp and Keenan Crane. 2020a. You can find geodesic paths in triangle meshes by just flipping edges. ACM Trans. on Graphics (TOG) 39, 6 (2020), 1–15.
37. Nicholas Sharp and Keenan Crane. 2020b. A Laplacian for Nonmanifold Triangle Meshes. Computer Graphics Forum (SGP) 39, 5 (2020).
38. Nicholas Sharp, Mark Gillespie, and Keenan Crane. 2021. Geometry Processing with Intrinsic Triangulations. (2021).
39. Nicholas Sharp, Yousuf Soliman, and Keenan Crane. 2019a. Navigating intrinsic triangulations. ACM Trans. on Graphics (TOG) 38, 4 (2019), 1–16.
40. Nicholas Sharp, Yousuf Soliman, and Keenan Crane. 2019b. The Vector Heat Method. ACM Trans. Graph. 38, 3 (2019).
41. Jonathan R Shewchuk. 1997. Delaunay refinement mesh generation. Ph.D. Dissertation. Carnegie-Mellon Univ School of Computer Science.
42. Gilbert Strang and George J Fix. 2008. An analysis of the finite element method (2 ed.). 212 (2008).
43. Jian Sun, Tianqi Wu, Xianfeng Gu, and Feng Luo. 2015. Discrete conformal deformation: algorithm and experiments. SIAM Journal on Imaging Sciences 8, 3 (2015), 1421–1456.
44. Ge Xia. 2013. The stretch factor of the Delaunay triangulation is less than 1.998. SIAM J. Comput. 42, 4 (2013), 1620–1659.
45. Qingnan Zhou, Eitan Grinspun, Denis Zorin, and Alec Jacobson. 2016. Mesh arrangements for solid geometry. ACM Transactions on Graphics (TOG) 35, 4 (2016), 1–15.
46. Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv preprint arXiv:1605.04797 (2016).