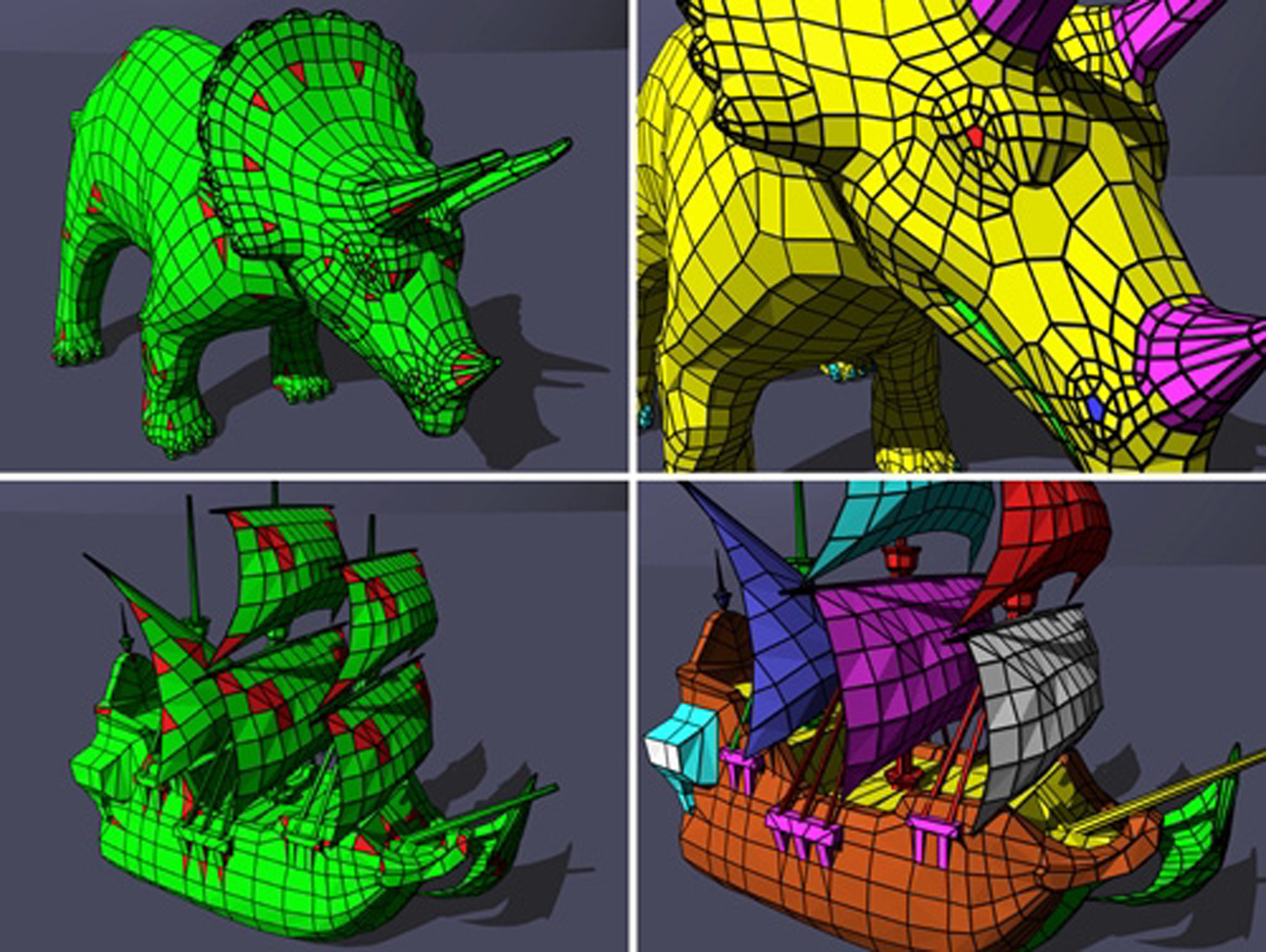
“Face fixer: compressing polygon meshes with properties” by Isenburg and Snoeyink

Most schemes to compress the topology of a surface mesh have been developed for the lowest common denominator: triangulated meshes. We propose a scheme that handles the topology of arbitrary polygon meshes. It encodes meshes directly in their polygonal representation and extends to capture face groupings in a natural way. Avoiding the triangulation step we reduce the storage costs for typical polygon models that have group structures and property data.

1. C. Bajaj, V. Pascucci, and G. Zhuang. Progressive compression and transmission of arbitrary triangular meshes. In Visualization 99, pages 307-316,1999.
2. D. Cohen-Or, D. Levin, and O. Remez. Progressive compression of arbitrary tri-angular meshes. In Visualization 99 Conference Proceedings, pages 67-72,1999.
3. M. Deering. Geometry compression. In SIGGRAPH 95, pages 13-20, 1995.
4. M. Denny and C. Sohler. Encoding a triangulation as a permutation of its point set. In Proc. of 9th Canadian Conf. on Comp. Geom., pages 39-43, 1997.
5. F. Evans, S. S. Skiena, and A. Varshney. Optimizing triangle strips for fast ren-dering. In Visualization 96 Conference Proceedings, pages 319-326, 1996.
6. L. Guibas and J. Stolfi. Primitives for the manipulation of general subdivisions and the computation of Voronoi Diagrams. ACM ToG, 4(2):74-123, 1985.
7. S. Gumhold and W. Strasser. Real time compression of triangle mesh connectiv-ity. In SIGGRAPH 98 Conference Proceedings, pages 133-140,1998.
8. H. Hoppe. Progressive meshes. In SIGGRAPH 96, pages 99-108, 1996.
9. M. Isenburg and J. Snoeyink. Mesh collapse compression. In Proceedings of SIBGRAPI 99, Campinas, Brazil, pages 27-28, 1999.
10. M. Isenburg and J. Snoeyink. Spirale reversi: Reverse decoding of the Edge-breaker encoding. Technical Report TR-99-08, Computer Science, UBC, 1999.
11. K. Keeler and J. Westbrook. Short encodings of planar graphs and maps. In Dis-crete Applied Mathematics, pages 239-252,1995.
12. D. King and J. Rossignac. Guaranteed 3.67v bit encoding of planar triangle graphs. In Proc. of 11th Canadian Conf. on Comp. Geom., pages 146-149,1999.
13. D. King, J. Rossignac, and A. Szymczak. Connectivity compression for irregular quadrilateral meshes. Technical Report TR-99-36,GVU, Georgia Tech, 1999.
14. D. G. Kirkpatrick. Optimal search in planar subdivisions. SIAMJournal of Com-puting, 12(1):28-35, 1983.
15. B. Kronrod and C. Gotsman. Efficient coding of non-triangular meshes. In Proc. of 16th Europ. Workshop on Computational Geometry, pages 24-26, 2000.
16. J. Li, C. C. Kuo, and H. Chen. Mesh connectivity coding by dual graph approach. Contribution Document MPEG98/m3530Tokyo, mar 1998.
17. R. Parajola and Rossignac. Compressed progressive meshes. Technical Report TR-99-05, GVU, Georgia Tech, 1999.
18. J. Rossignac. Edgebreaker: Connectivity compressionfor triangle meshes. IEEE Transactions on Visualization and Computer Graphics, 5(1), 1999.
19. J. Rossignac and A. Szymczak. Wrap&zip: Linear decoding of planar triangle graphs. The Journal of ComputationalGeometry, Theory and Applications, 1999.
20. J. Snoeyink and M. van Kreveld. Linear-time reconstruction of Delaunay trian-gulations with applications. In Proc. of Europ. Symp. Alg., pages 459-471,1997.
21. D. M. Y. Sommerville. An Introductionto the Geometry of N Dimensions. Dutton Publications, New York, 1929.
22. G. Taubin, A. Gu~ eziec, W.P. Horn, and F. Lazarus. Progressive forest split com-pression. In SIGGRAPH 98 Conference Proceedings, pages 123-132, 1998.
23. G. Taubin, W.P. Horn, F. Lazarus, and J. Rossignac. Geometry coding and VRML. Proceedings of the IEEE, 86(6):1228-1243, 1998.
24. G. Taubin and J. Rossignac. Geometric compression throughtopological surgery. ACM Transactions on Graphics, 17(2):84-115, 1998.
25. C. Touma and C. Gotsman. Triangle mesh compression. In Graphics Interface 98 Conference Proceedings, pages 26-34, 1998.
26. G. Turan. Succinct representations of graphs. Dis. Apl. Math., 8:289-294, 1984.
27. W.T. Tutte. A census of planar triangulations. Cnd. Jrn. Math., 14:21-38, 1962.
28. Viewpoint. Premier Catalog (2000 Edition) www.viewpoint.com.
29. I. H. Witten, R. M. Neal, and J. G. Cleary. Arithmetic coding for data compres-sion. Communications of the ACM, 30(6):520-540, 1987.
30. M. Woo, J. Neider, and T. Davis. Open GL Programming Guide. A.W., 1996.