“Estimating Discrete Total Curvature with Per Triangle Normal Variation” by Chen
Conference:
Type(s):
Interest Area:
- New Technologies, Production & Animation, and Research / Education
Title:
- Estimating Discrete Total Curvature with Per Triangle Normal Variation
Session/Category Title: Byte-Size Geometry; Mathematical Techniques
Presenter(s)/Author(s):
Abstract:
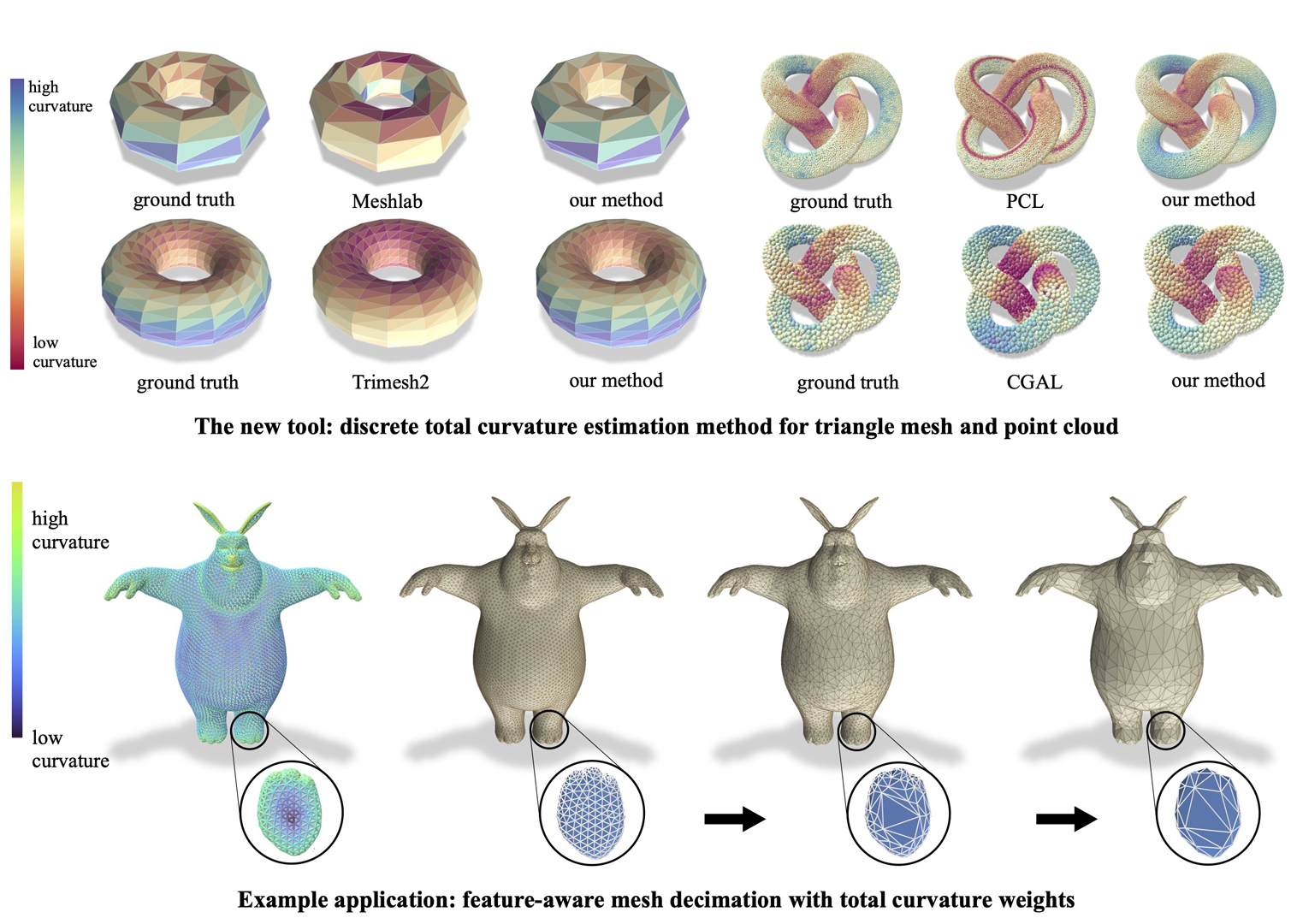
We introduce a novel approach for measuring the total curvature at every triangle of a discrete surface. This method takes advantage of the relationship between per triangle total curvature and the Dirichlet energy of the Gauss map. This new tool can be used on both triangle meshes and point clouds and has numerous applications. In this study, we demonstrate the effectiveness of our technique by using it for feature-aware mesh decimation, and show that it outperforms existing curvature-estimation methods from popular libraries such as Meshlab, Trimesh2, and Libigl. When estimating curvature on point clouds, our method outperforms popular libraries PCL and CGAL.
References:
[1] Mikhail Belkin, Jian Sun, and Yusu Wang. 2008. Discrete Laplace operator on meshed surfaces. In Proceedings of the twenty-fourth annual symposium on Computational geometry. 278–287.
[2] Quentin Mérigot, Maks Ovsjanikov, and Leonidas J Guibas. 2010. Voronoi-based curvature and feature estimation from point clouds. IEEE Transactions on Visualization and Computer Graphics 17, 6 (2010), 743–756.
[3] Daniele Panozzo, Enrico Puppo, and Luigi Rocca. 2010. Efficient multi-scale curvature and crease estimation. Proceedings of Computer Graphics, Computer Vision and Mathematics (Brno, Czech Rapubic 1, 6 (2010).
[4] Szymon Rusinkiewicz. 2004. Estimating curvatures and their derivatives on triangle meshes. In Proceedings. 2nd International Symposium on 3D Data Processing, Visualization and Transmission, 2004. 3DPVT 2004. IEEE, 486–493.
[5] Gabriel Taubin. 1995. Estimating the tensor of curvature of a surface from a polyhedral approximation. In Proceedings of IEEE International Conference on Computer Vision. IEEE, 902–907.
[6] Max Wardetzky, Miklós Bergou, David Harmon, Denis Zorin, and Eitan Grinspun. 2007. Discrete quadratic curvature energies. Computer Aided Geometric Design 24, 8-9 (2007), 499–518.
ACM Digital Library Publication:
Overview Page:
Submit a story:
If you would like to submit a story about this presentation, please contact us: historyarchives@siggraph.org
