“Designing unreinforced masonry models” by Panozzo, Block and Sorkine-Hornung
Conference:
Type(s):
Title:
- Designing unreinforced masonry models
Session/Category Title: Building Structures & Layouts
Presenter(s)/Author(s):
Moderator(s):
Abstract:
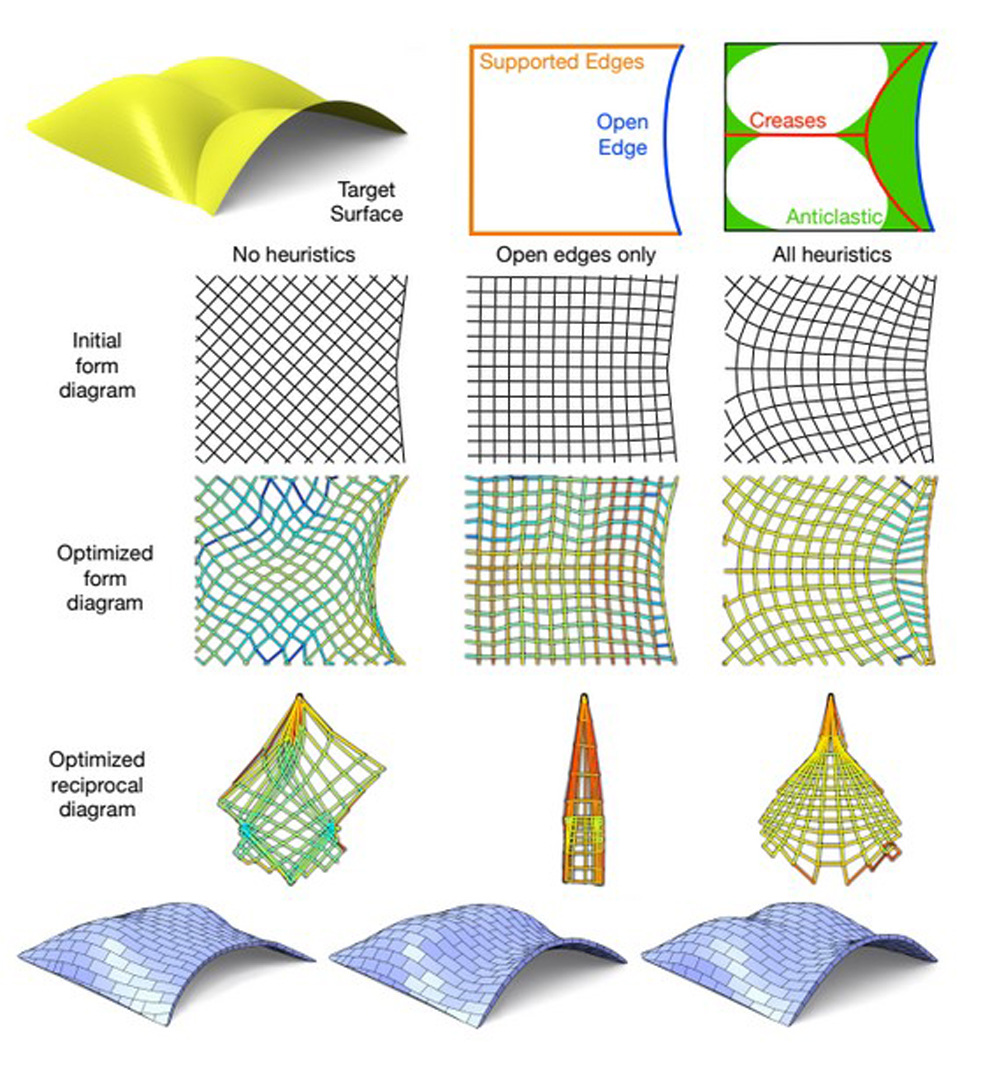
We present a complete design pipeline that allows non-expert users to design and analyze masonry structures without any structural knowledge. We optimize the force layouts both geometrically and topologically, finding a self-supported structure that is as close as possible to a given target surface. The generated structures are tessellated into hexagonal blocks with a pattern that prevents sliding failure. The models can be used in physically plausible virtual environments or 3D printed and assembled without reinforcements.
References:
1. Bhooshan, S., and El Sayed, M. 2011. Use of subdivision surfaces in architectural form-finding and procedural modelling. In Proc. Symp. Simulation for Architecture and Urban Design. Google ScholarDigital Library
2. Block, P., and Lachauer, L. 2012. Three-dimensional equilibrium analysis of gothic masonry vaults. In Proc. VIII Int. Conference on Structural Analysis of Historic Construction.Google Scholar
3. Block, P. 2009. Thrust Network Analysis: Exploring Three-dimensional Equilibrium. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA, USA.Google Scholar
4. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3, 77. Google ScholarDigital Library
5. Borgart, A. 2005. The relationship of form and force in (irregular) curved surfaces. In Proc. Int. Conf. Computation of Shell and Spatial Structures.Google Scholar
6. Bouaziz, S., Deuss, M., Schwartzburg, Y., Weise, T., and Pauly, M. 2012. Shape-up: Shaping discrete geometry with projections. Comput. Graph. Forum 31, 5, 1657–1667. Google ScholarDigital Library
7. Calladine, C. R. 1983. Theory of Shell Structures. Cambridge University Press, Cambridge.Google Scholar
8. Cazals, F., and Pouget, M. 2003. Estimating differential quantities using polynomial fitting of osculating jets. In Proc. SGP. Google ScholarDigital Library
9. Crane, K., Desbrun, M., and Schröder, P. 2010. Trivial connections on discrete surfaces. Comput. Graph. Forum 29, 5.Google ScholarCross Ref
10. Eigensatz, M., Kilian, M., Schiftner, A., Mitra, N. J., Pottmann, H., and Pauly, M. 2010. Paneling architectural freeform surfaces. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
11. Fraternali, F. 2010. A thrust network approach to the equilibrium problem of unreinforced masonry vaults via polyhedral stress functions. Mechanics Research Communications 37, 2.Google ScholarCross Ref
12. Fu, C.-W., Lai, C.-F., He, Y., and Cohen-Or, D. 2010. K-set tilable surfaces. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
13. Heyman, J. 1995. The Stone Skeleton: Structural engineering of masonry architecture. Cambridge University Press.Google Scholar
14. Hildebrandt, K., Polthier, K., and Wardetzky, M. 2005. Smooth feature lines on surface meshes. In Proc. SGP. Google ScholarDigital Library
15. Kilian, A., and Ochsendorf, J. 2005. Particle-spring systems for structural form finding. J. IASS 148, 77.Google Scholar
16. Liu, Y., Pottmann, H., Wallner, J., Yang, Y.-L., and Wang, W. 2006. Geometric modeling with conical meshes and developable surfaces. ACM Trans. Graph. 25, 3, 681–689. Google ScholarDigital Library
17. Mark, R. 1982. Experiments in Gothic structure. The MIT Press, Cambridge.Google Scholar
18. O’Dwyer, D. W. 1999. Funicular analysis of masonry vaults. Computers and Structures 73, 1–5.Google Scholar
19. Panozzo, D., Lipman, Y., Puppo, E., and Zorin, D. 2012. Fields on symmetric surfaces. ACM Trans. Graph. 31, 4. Google ScholarDigital Library
20. Ray, N., Vallet, B., Li, W., and Lévy, B. 2008. N-Symmetry Direction Field Design. ACM Trans. Graph. 27, 2. Google ScholarDigital Library
21. Rippmann, M., and Block, P. 2013. Rethinking structural masonry: unreinforced, stone-cut shells. In Proc. ICE – Construction Materials.Google Scholar
22. Rippmann, M., Lachauer, L., and Block, P. 2012. Interactive vault design. International Journal of Space Structures 27, 4, 219–230.Google ScholarCross Ref
23. Schiftner, A., and Balzer, J. 2010. Statics-sensitive layout of planar quadrilateral meshes. In Proc. Advances in Architectural Geometry, 221–236.Google Scholar
24. Shewchuk, J. R. 1996. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In Applied Computational Geometry: Towards Geometric Engineering, vol. 1148 of Lecture Notes in Computer Science. Springer-Verlag, 203–222. Google ScholarDigital Library
25. Singh, M., and Schaefer, S. 2010. Triangle surfaces with discrete equivalence classes. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
26. Van Mele, T., McInerney, J., DeJong, M., and Block, P. 2012. Physical and computational discrete modeling of masonry vault collapse. In Proc. Int. Conf. Structural Analysis of Historical Constructions.Google Scholar
27. Vouga, E., Höbinger, M., Wallner, J., and Pottmann, H. 2012. Design of self-supporting surfaces. ACM Trans. Graph. 31, 4. Google ScholarDigital Library
28. Whiting, E., Ochsendorf, J., and Durand, F. 2009. Procedural modeling of structurally-sound masonry buildings. ACM Trans. Graph. 28, 5, 112:1–112:9. Google ScholarDigital Library
29. Whiting, E., Shin, H., Wang, R., Ochsendorf, J., and Durand, F. 2012. Structural optimization of 3D masonry buildings. ACM Trans. Graph. 31, 6, 159:1–159:11. Google ScholarDigital Library
30. Williams, C. J. K. 1990. The generation of a class of structural forms for vaults and sails. The Structural Engineer 68, 12.Google Scholar
31. Zessin, J., Lau, W., and Ochsendorf, J. 2010. Equilibrium of cracked masonry domes. Proc. ICE-Engineering and Computational Mechanics 163, 3, 135–145.Google Scholar
32. Zimmer, H., Campen, M., Bommes, D., and Kobbelt, L. 2012. Rationalization of triangle-based point-folding structures. Comput. Graph. Forum 31, 2, 611–620. Google ScholarDigital Library