“Design galleries: a general approach to setting parameters for computer graphics and animation” by Marks, Andalman, Beardsley, Freeman, Gibson, et al. …

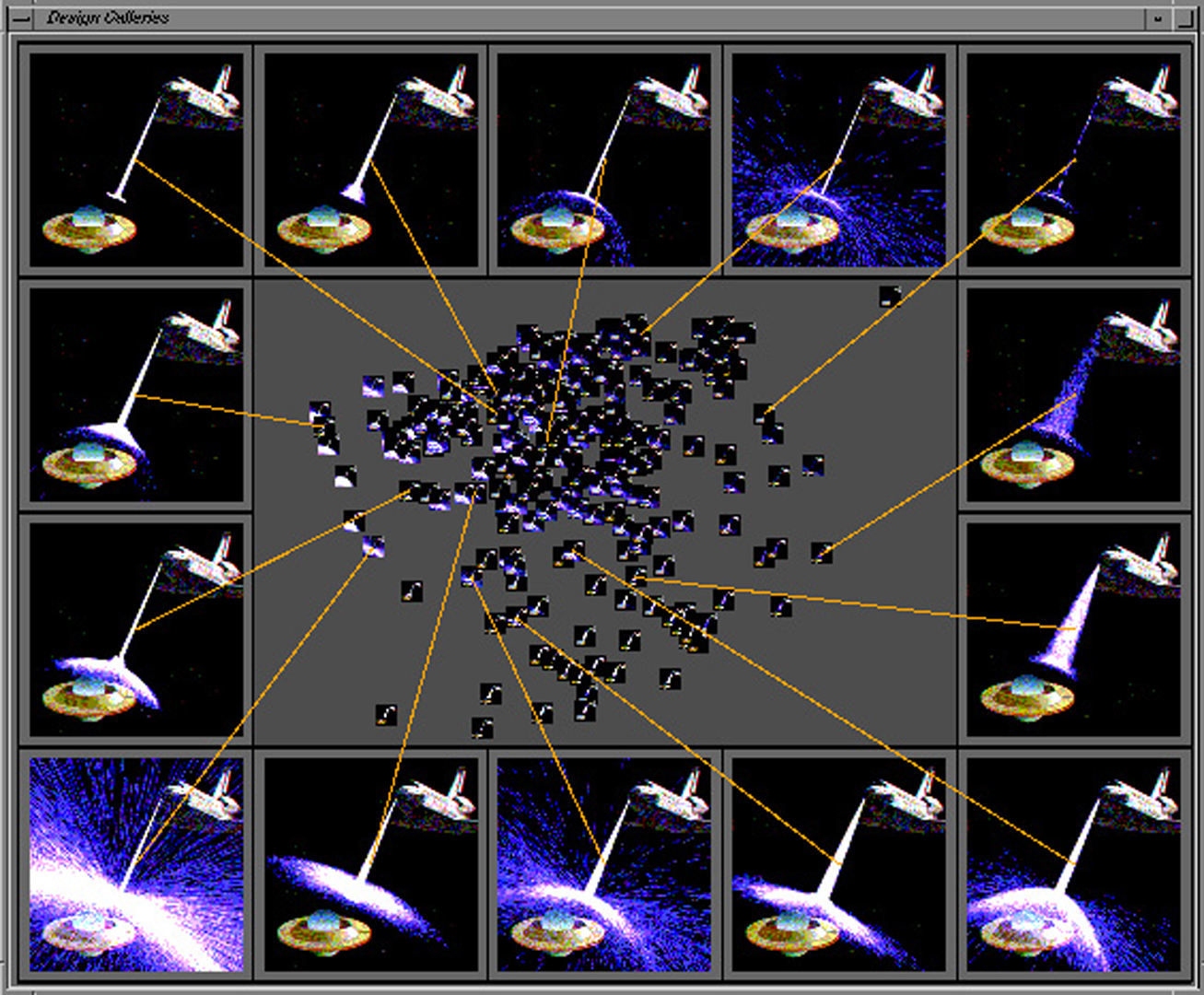
Image rendering maps scene parameters to output pixel values; animation maps motion-control parameters to trajectory values. Because these mapping functions are usually multidimensional, nonlinear, and discontinuous, finding input parameters that yield desirable output values is often a painful process of manual tweaking. Interactive evolution and inverse design are two general methodologies for computer-assisted parameter setting in which the computer plays a prominent role. In this paper we present another such methodology. Design GalleryTM (DG) interfaces present the user with the broadest selection, automatically generated and organized, of perceptually different graphics or animations that can be produced by varying a given input-parameter vector. The principal technical challenges posed by the DG approach are dispersion, finding a set of input-parameter vectors that optimally disperses the resulting output-value vectors, and arrangement, organizing the resulting graphics for easy and intuitive browsing by the user. We describe the use of DG interfaces for several parameter-setting problems: light selection and placement for image rendering, both standard and image-based; opacity and color transfer-function specification for volume rendering; and motion control for particle-system and articulated-figure animation.

1. C.J. Alpert and A. B. Kahng. Recent directions in netlist partitioning: a survey. Integration: The VLSI Journal, 19:1-81, 1995.
2. E A. Beardsley, A. E Zisserman, and D. W. Murray. Sequential updating of projective and affine structure from motion. International Journal of Computer Vision, 1997. In press.
3. I. Borg and E Groenen. Modern Multidimensional Scaling: Theo17 and Applications. Springer, 1997.
4. M. R. Garey, D. S. Johnson, and L. Stockmeyer. Some simplified NP-complete graph problems. Theoretical Computer Science, 1(3):237-267, 1976.
5. J.C. Gower. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika, 53:325- 338, 1966.
6. P. Haeberli. Synthetic lighting for photography. URL http://- www.sgi.com/grafica/synth/index.html, Jan. 1992.
7. T. He, L. Hong, A. Kaufman, and H. Pfister. Generation of transfer functions with stochastic search techniques. In Proc. of Visualization 96, pages 227-234, San Francisco, California, Oct. 1996.
8. J. Kahrs, S. Calahan, D. Carson, and S. Poster. Pixel cinematography: a lighting approach for computer graphics. Notes for Course #30, SIGGRAPH 96, New Orleans, Louisiana, Aug. 1996.
9. G. Karypis and V. Kumar. Multilevel k-way partitioning scheme for irregular graphs. Technical report, Dept. of Computer Science, Univ. of Minnesota, 1995. See also URL http://- www.cs.umn.edu/”karypis/metis/metis.html.
10. J.K. Kawai, J. S. Painter, and M. F. Cohen. Radioptimization – goal-based rendering. In SIGGRAPH 93 Conf. Proc., pages 147-154, Anaheim, California, Aug. 1993.
11. S. Kochhar. A prototype system for design automation via the browsing paradigm. In Proc. of Graphics Intelface 90, pages 156-166, Halifax, Nova Scotia, May 1990.
12. Z. Liu, S. J. Gortler, and M. F. Cohen. Hierarchical spacetime control. In SIGGRAPH 94 Conf. Proc., pages 35-42, Orlando, Florida, July 1994.
13. H. Murakami and B. V. K. V. Kumar. Efficient calculation of primary images from a set of images. IEEE Trans. on Pattern Analysis and Machine Intelligence, PAMI-4(5):511-515, Sept. 1982.
14. J. T. Ngo and J. Marks. Spacetime constraints revisited. In SIGGRAPH 93 Conf. Proc., pages 343-350, Anaheim, California, Aug. 1993.
15. E Poulin and A. Fournier. Lights from highlights and shadows. In Proc. of the 1992 Symposium on Interactive Graphics, pages 31-38, Boston, Massachusetts,Mar. 1992. In Computer Graphics 25(2), 1992.
16. W. T. Reeves. Particle systems- a technique for modeling a class of fuzzy objects. ACM Trans. on Graphics, 2:91-108, Apr. 1983.
17. D.E. Rosenthal and M. A. Sherman. High performance multibody simulations via symbolic equation manipulation and Kane’s method. Journal of Astronautical Sciences, 34(3):223- 239, 1986.
18. Y. Rubner, L. J. Guibas, and C. Tomasi. The earth mover’s distance, multi-dimensional scaling, and color-based image retrieval. In Proc. of the DARPA Image Understanding Workshop, New Orleans, May 1997.
19. C. Schoeneman, J. Dorsey, B. Smits, J. Arvo, and D. Greenberg. Painting with light. In SIGGRAPH 93 Conf. Proc., pages 143-146, Anaheim, California, Aug. 1993.
20. T. Shinbrot, C. Grebogi, J. Wisdom, and J. A. Yorke. Chaos in a double pendulum. American Journal of Physics, 60(6):491- 499, 1992.
21. K. Sims. Artificial evolution for computer graphics. In Computer Graphics (SIGGRAPH 91 Conf. Proc.), volume 25, pages 319-328, Las Vegas, Nevada, July 1991.
22. K. Sims. Evolving virtual creatures. In SIGGRAPH 94 Conf. Proc., pages 15-22, Orlando, Florida, July 1994.
23. S. Todd and W. Latham. Evolutiona~7 Art and Computers. Academic Press, London, 1992.
24. W. S. Torgerson. Theo17 and Methods of Scaling. Wiley, New York, 1958. See especially pages 254-259.
25. M. van de Panne and E. Fiume. Sensor-actuator networks. In SIGGRAPH 93 Conf. Proc., pages 335-342, Anaheim, California, Aug. 1993.
26. J. Ventrella. Disney meets Darwin – the evolution of funny animated figures. In Proc. of Computer Animation 95, pages 35-43, Apr. 1995.
27. A. Witkin and M. Kass. Spacetime constraints. In Computer Graphics (SIGGRAPH 88 Conf. Proc.), volume 22, pages 159-168, Atlanta, Georgia, Aug. 1988.