“Construction and fabrication of reversible shape transforms” – ACM SIGGRAPH HISTORY ARCHIVES

“Construction and fabrication of reversible shape transforms”

  • 2018 SA Technical Papers_Li_Construction and fabrication of reversible shape transforms

Conference:


Type(s):


Title:

    Construction and fabrication of reversible shape transforms

Session/Category Title:   Fun in geometry & fabrication

Presenter(s)/Author(s):


Moderator(s):


Abstract:


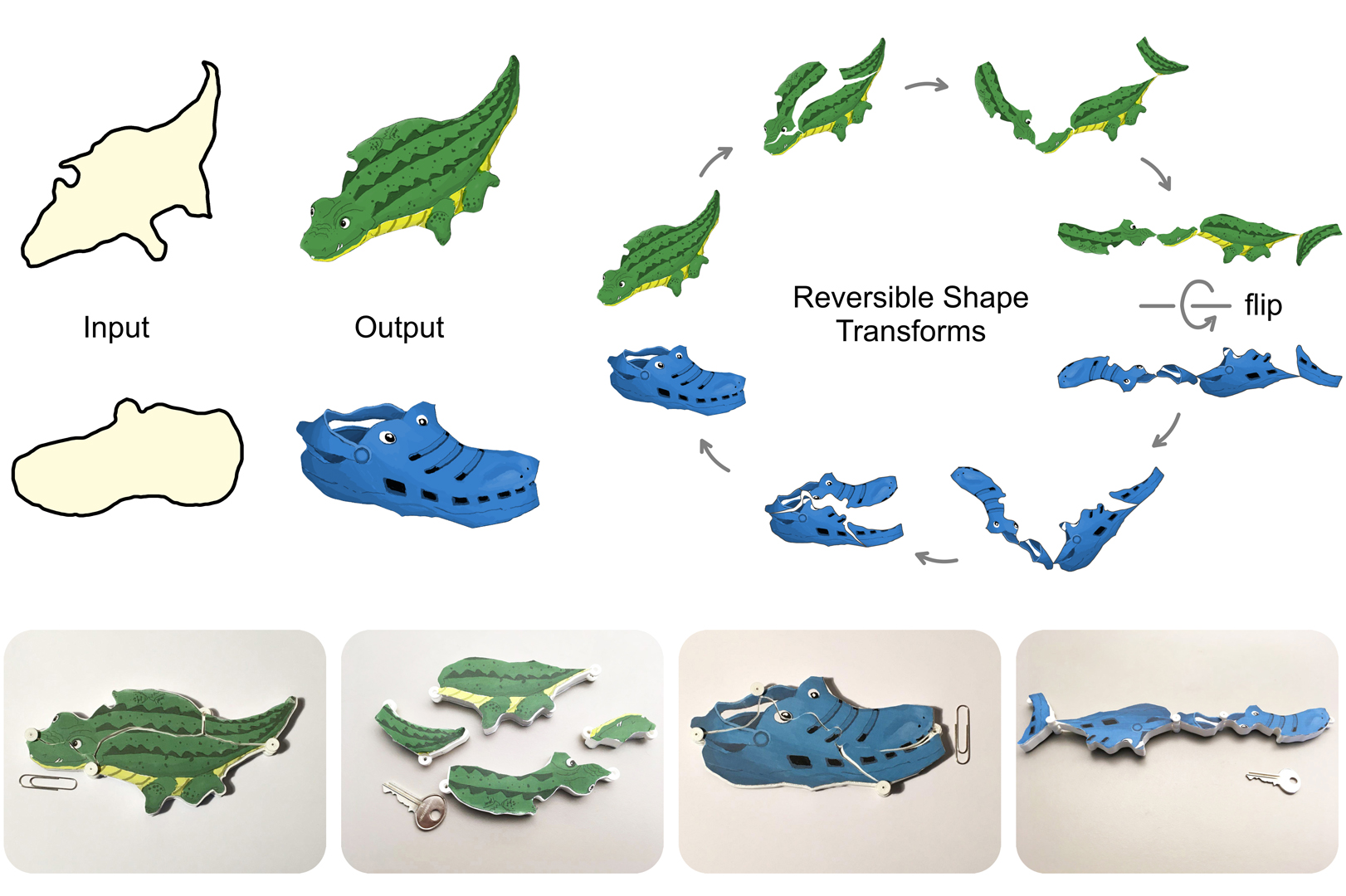
    We study a new and elegant instance of geometric dissection of 2D shapes: reversible hinged dissection, which corresponds to a dual transform between two shapes where one of them can be dissected in its interior and then inverted inside-out, with hinges on the shape boundary, to reproduce the other shape, and vice versa. We call such a transform reversible inside-out transform or RIOT. Since it is rare for two shapes to possess even a rough RIOT, let alone an exact one, we develop both a RIOT construction algorithm and a quick filtering mechanism to pick, from a shape collection, potential shape pairs that are likely to possess the transform. Our construction algorithm is fully automatic. It computes an approximate RIOT between two given input 2D shapes, whose boundaries can undergo slight deformations, while the filtering scheme picks good inputs for the construction. Furthermore, we add properly designed hinges and connectors to the shape pieces and fabricate them using a 3D printer so that they can be played as an assembly puzzle. With many interesting and fun RIOT pairs constructed from shapes found online, we demonstrate that our method significantly expands the range of shapes to be considered for RIOT, a seemingly impossible shape transform, and offers a practical way to construct and physically realize these transforms.

References:


    1. Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine, and Scott D. Kominers. 2012. Hinged dissections exist. Discrete & Computational Geometry 47, 1 (2012), 150–186.Google ScholarDigital Library
    2. Jin Akiyama, Stefan Langerman, and Kiyoko Matsunaga. 2015. Reversible nets of polyhedra. In Japanese Conference on Discrete and Computational Geometry and Graphs. Springer, 13–23.Google Scholar
    3. Jin Akiyama and Kiyoko Matsunaga. 2015. Treks into Intuitive Geometry. Springer.Google Scholar
    4. Jin Akiyama and Kiyoko Matsunaga. 2017. Generalization of Haberdasher’s Puzzle. Discrete & Computational Geometry 58, 1 (2017), 30–50. Google ScholarDigital Library
    5. Jin Akiyama and Gisaku Nakamura. 2000. Dudeney Dissections of Polygons and Polyhedrons-A Survey-. In Japanese Conference on Discrete and Computational Geometry. Springer, 1–30. Google ScholarDigital Library
    6. Tyler Andrews. 2012. Computation time comparison between matlab and C++ using launch windows. Research report submitted to American Institute of Aeronautics and Astronautics, California Polytechnic State University San Luis Obispo (2012).Google Scholar
    7. Xiang Bai, Wenyu Liu, and Zhuowen Tu. 2009. Integrating contour and skeleton for shape classification. In Proc. ICCV. IEEE, 360–367.Google ScholarCross Ref
    8. Yurii D. Burago and Viktor A. Zalgaller. 2013. Geometric inequalities. Vol. 285. Springer Science & Business Media.Google Scholar
    9. Xuelin Chen, Hao Zhang, Jinjie Lin, Ruizhen Hu, Lin Lu, Qixing Huang, Bedrich Benes, Daniel Cohen-Or, and Baoquan Chen. 2015. Dapper: Decompose-and-Pack for 3D Printing. ACM Trans. on Graphics (Proc. of SIGGRAPH Asia) 34, 6 (2015), 213:1–213:12. Google ScholarDigital Library
    10. Erik D. Demaine, Martin L. Demaine, David Eppstein, Greg N. Frederickson, and Erich Friedman. 2005. Hinged Dissection of Polyominoes and Polyforms. Computational Geometry 31, 3 (2005), 237–262. Google ScholarDigital Library
    11. David H. Douglas and Thomas K. Peucker. 1973. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica: The International Journal for Geographic Information and Geovisualization 10, 2 (1973), 112–122.Google ScholarCross Ref
    12. Henry E. Dudeney. 1902. Puzzles and prizes. Column in the Weekly Dispatch, April 19, 1896-March 27, 1904 (1902).Google Scholar
    13. Noah Duncan, Lap-Fai Yu, Sai-Kit Yeung, and Demetri Terzopoulos. 2017. Approximate Dissections. ACM Trans. on Graph. 36, 6, Article 182 (Nov. 2017), 13 pages. Google ScholarDigital Library
    14. Thomas Eiter and Heikki Mannila. 1994. Computing discrete Fréchet distance. Technical Report. Tech. Report CD-TR 94/64, Information Systems Department, Technical University of Vienna.Google Scholar
    15. Greg N. Frederickson. 1997. Dissections: Plane and Fancy. Cambridge University Press.Google ScholarCross Ref
    16. Greg N. Frederickson. 2002. Hinged Dissections: Swinging and Twisting. Cambridge University Press.Google Scholar
    17. RJ Gardner. 1985. A problem of Sallee on equidecomposable convex bodies. Proc. Amer. Math. Soc. 94, 2 (1985), 329–332.Google ScholarCross Ref
    18. Longin Jan Latecki, Rolf Lakamper, and T Eckhardt. 2000. Shape descriptors for non-rigid shapes with a single closed contour. In IEEE CVPR, Vol. 1. IEEE, 424–429.Google ScholarCross Ref
    19. Xian-Ying Li, Tao Ju, Yan Gu, and Shi-Min Hu. 2011. A geometric study of v-style pop-ups: theories and algorithms. In ACM Trans. on Graph., Vol. 30. ACM, 98. Google ScholarDigital Library
    20. Maarten Löffler, Mira Kaiser, Tim van Kapel, Gerwin Klappe, Marc van Kreveld, and Frank Staals. 2014. The Connect-The-Dots Family of Puzzles: Design and Automatic Generation. ACM Trans. on Graph. 33, 4, Article 72 (2014), 72:1–72:10 pages. Google ScholarDigital Library
    21. Nobuyuki Otsu. 1979. A threshold selection method from gray-level histograms. IEEE transactions on systems, man, and cybernetics 9, 1 (1979), 62–66.Google ScholarCross Ref
    22. Ariel Shamir. 2008. A survey on mesh segmentation techniques. Computer Graphics Forum 27, 6 (2008), 1539–1556.Google ScholarCross Ref
    23. Peng Song, Chi-Wing Fu, Yueming Jin, Hongfei Xu, Ligang Liu, Pheng-Ann Heng, and Daniel Cohen-Or. 2017. Reconfigurable Interlocking Furniture. ACM Trans. on Graph. 36, 6, Article 174 (Nov. 2017), 14 pages. Google ScholarDigital Library
    24. Olga Sorkine, Daniel Cohen-Or, Yaron Lipman, Marc Alexa, Christian Rössl, and H-P Seidel. 2004. Laplacian surface editing. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing. ACM, 175–184. Google ScholarDigital Library
    25. Timothy Sun and Changxi Zheng. 2015. Computational Design of Twisty Joints and Puzzles. ACM Trans. on Graph. 34, 4, Article 101 (2015), 101:1–101:11 pages. Google ScholarDigital Library
    26. Nobuyuki Umetani, Danny M. Kaufman, Takeo Igarashi, and Eitan Grinspun. 2011. Sensitive couture for interactive garment modeling and editing. ACM Trans. on Graph. 30, 4 (2011), 90–1. Google ScholarDigital Library
    27. William Wallace. 1831. Elements of Geometry (8th ed.). Bell & Bradfute.Google Scholar
    28. Shiqing Xin, Chi-Fu Lai, Chi-Wing Fu, Tien-Tsin Wong, Ying He, and Daniel Cohen-Or. 2011. Making Burr Puzzles from 3D Models. ACM Trans. on Graph. 30, 4, Article 97 (2011), 97:1–97:8 pages. Google ScholarDigital Library
    29. Christopher Yu, Keenan Crane, and Stelian Coros. 2017. Computational Design of Telescoping Structures. ACM Trans. on Graph. 36, 4, Article 83 (July 2017), 9 pages. Google ScholarDigital Library
    30. Yahan Zhou, Shinjiro Sueda, Wojciech Matusik, and Ariel Shamir. 2014. Boxelization: folding 3D objects into boxes. ACM Trans. on Graph. 33, 4 (2014), 71. Google ScholarDigital Library
    31. Yahan Zhou and Rui Wang. 2012. An Algorithm for Creating Geometric Dissection Puzzles. In Proc. of Bridges Conf. 49–58.Google Scholar
    32. Changqing Zou, Junjie Cao, Warunika Ranaweera, Ibraheem Alhashim, Ping Tan, Alla Sheffer, and Hao Zhang. 2016. Legible Compact Calligrams. ACM Trans. on Graph. 35, 4, Article 122 (July 2016), 122:1–122:12 pages. Google ScholarDigital Library
    33. Jovisa Zunic and Paul L. Rosin. 2004. A new convexity measure for polygons. IEEE Trans. Pattern Analysis & Machine Intelligence 26, 7 (2004), 923–934. Google ScholarDigital Library

ACM Digital Library Publication:


Overview Page:


Submit a story:

If you would like to submit a story about this presentation, please contact us: historyarchives@siggraph.org