“Cascaded Sobol’ sampling” by Paulin, Coeurjolly, Iehl, Bonneel, Keller, et al. …
Conference:
Type(s):
Title:
- Cascaded Sobol' sampling
Session/Category Title:
- Samping and Denoising
Presenter(s)/Author(s):
Abstract:
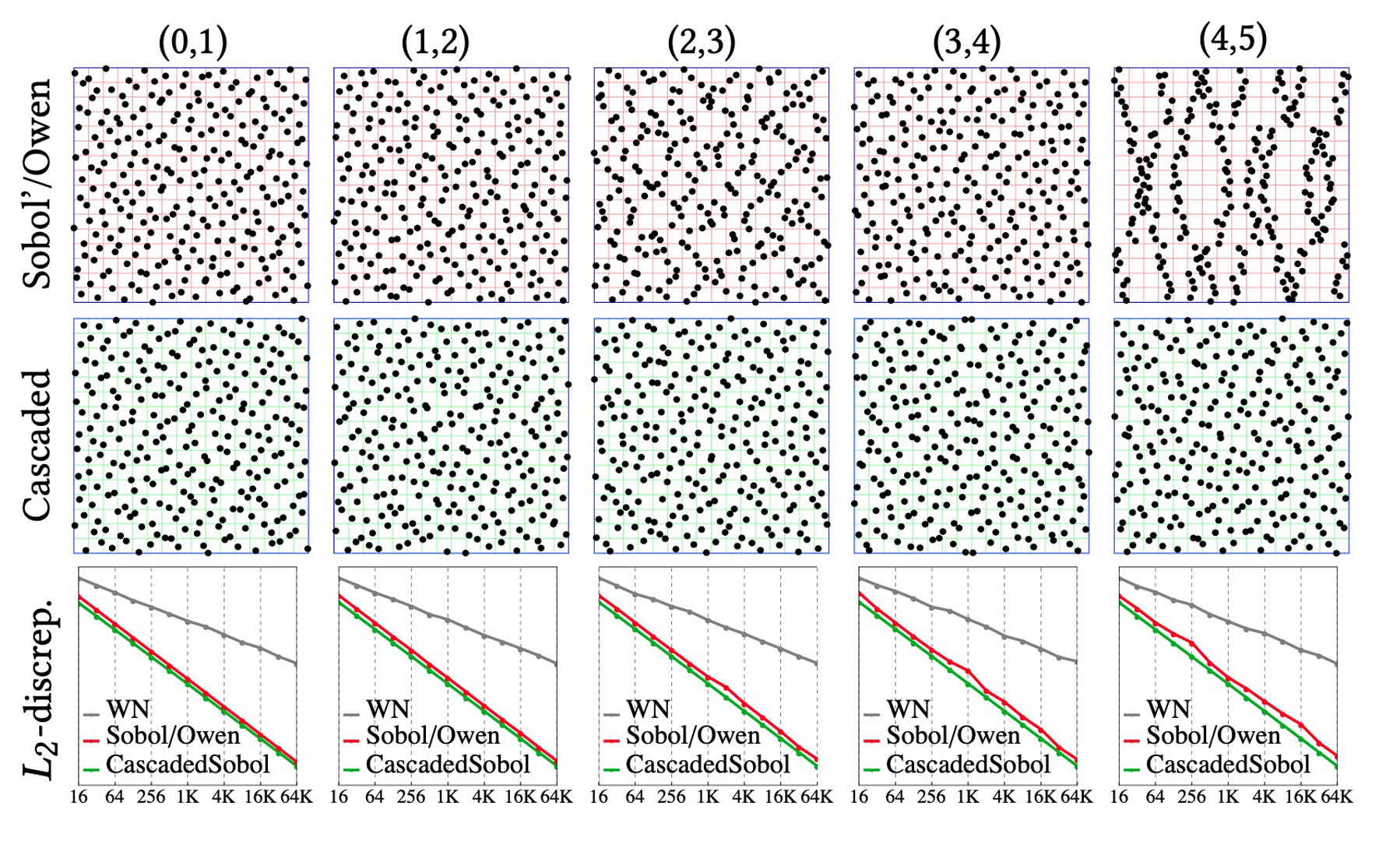
Rendering quality is largely influenced by the samplers used in Monte Carlo integration. Important factors include sample uniformity (e.g., low discrepancy) in the high-dimensional integration domain, sample uniformity in lower-dimensional projections, and lack of dominant structures that could result in aliasing artifacts. A widely used and successful construction is the Sobol’ sequence that guarantees good high-dimensional uniformity and consequently results in faster convergence of quasi-Monte Carlo integration. We show that this sequence exhibits low uniformity and dominant structures in low-dimensional projections. These structures impair quality in the context of rendering, as they precisely occur in the 2-dimensional projections used for sampling light sources, reflectance functions, or the camera lens or sensor. We propose a new cascaded construction, which, despite dropping the sequential aspect of Sobol’ samples, produces point sets exhibiting provably perfect dyadic partitioning (and therefore, excellent uniformity) in consecutive 2-dimensional projections, while preserving good high-dimensional uniformity. By optimizing the initialization parameters and performing Owen scrambling at finer levels of binary representations, we further improve over Sobol’s integration convergence rate. Our method does not incur any overhead as compared to the generation of the Sobol’ sequence, is compatible with Owen scrambling and can be used in rendering applications.
References:
1. Abdalla GM Ahmed, Hélène Perrier, David Coeurjolly, Victor Ostromoukhov, Jianwei Guo, Dong-Ming Yan, Hui Huang, and Oliver Deussen. 2016. Low-discrepancy blue noise sampling. ACM Trans. Graph. 35, 6 (2016), 247.
2. Abdalla GM Ahmed and Peter Wonka. 2020. Screen-space blue-noise diffusion of Monte Carlo sampling error via hierarchical ordering of pixels. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1–15.
3. Michael Balzer, Thomas Schlömer, and Oliver Deussen. 2009. Capacity-constrained point distributions: a variant of Lloyd’s method. ACM Trans. Graph. 28, 3 (2009).
4. Benedikt Bitterli. 2016. Rendering resources. https://benedikt-bitterli.me/resources/.
5. Robert Bridson. 2007. Fast Poisson Disk Sampling in Arbitrary Dimensions. In ACM SIGGRAPH Sketches. 22–23.
6. Brent Burley. 2020. Practical Hash-based Owen Scrambling. Journal of Computer Graphics Techniques (JCGT) 10, 4 (2020), 1–20.
7. Per Christensen, Andrew Kensler, and Charlie Kilpatrick. 2018. Progressive Multi-Jittered Sample Sequences. Computer Graphics Forum 37, 4 (2018), 21–33.
8. Roy Cranley and Thomas NL Patterson. 1976. Randomization of number theoretic methods for multiple integration. SIAM J. Numer. Anal. 13, 6 (1976), 904–914.
9. Josef Dick and Friedrich Pillichshammer. 2010. Digital Nets and Sequences: Discrepancy Theory and Quasi-Monte Carlo Integration. Cambridge University Press.
10. Raanan Fattal. 2011. Blue-Noise Point Sampling Using Kernel Density Model. ACM Trans. Graph. 30 (2011), 48:1–48:12.
11. Iliyan Georgiev and Marcos Fajardo. 2016. Blue-Noise Dithered Sampling. 35:1–35:1.
12. Leonhard Grünschloß, Johannes Hanika, Ronnie Schwede, and Alexander Keller. 2008. (t, m, s)-Nets and Maximized Minimum Distance. In Monte Carlo and Quasi-Monte Carlo Methods 2006. Springer, 397–412.
13. Leonhard Grünschloß, Matthias Raab, and Alexander Keller. 2012. Enumerating Quasi-Monte Carlo Point Sequences in Elementary Intervals. In Monte Carlo and Quasi-Monte Carlo Methods 2010, Leszek Plaskota and Henryk Woźniakowski (Eds.). Springer, 399–408.
14. John Halton. 1964. Radical-inverse quasi-random point sequence [G5]. Comm. ACM 7, 12 (1964), 701–702.
15. Daniel Heck, Thomas Schlömer, and Oliver Deussen. 2013. Blue Noise Sampling with Controlled Aliasing. ACM Trans. Graph. 32, 3 (2013), 25:1–25:12. Eric Heitz and Laurent Belcour. 2019. Distributing Monte Carlo Errors as a Blue Noise in Screen Space by Permuting Pixel Seeds Between Frames. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 149–158.
16. Eric Heitz, Laurent Belcour, Victor Ostromoukhov, David Coeurjolly, and Jean-Claude Iehl. 2019. A Low-Discrepancy Sampler that Distributes Monte Carlo Errors as a Blue Noise in Screen Space. In ACM SIGGRAPH Talk.
17. Fred Hickernell. 1998. A generalized discrepancy and quadrature error bound. Math. Comp. 67, 221 (1998), 299–322.
18. Edmund Hlawka. 1961. Funktionen von beschränkter Variation in der Theorie der Gleichverteilung. Annali di Matematica Pura ed Applicata 54, 1 (1961), 325–333.
19. Wojciech Jarosz, Afnan Enayet, Andrew Kensler, Charlie Kilpatrick, and Per Christensen. 2019. Orthogonal Array Sampling for Monte Carlo Rendering. Computer Graphics Forum 38, 4 (2019), 135–147.
20. Stephen Joe and Frances Kuo. 2008. Constructing Sobol’ sequences with better two-dimensional projections. SIAM J. on Scientific Computing 30, 5 (2008), 2635–2654.
21. Alexander Keller. 2004. Stratification by rank-1 lattices. In Monte Carlo and Quasi-Monte Carlo Methods 2002, Harald Niederreiter (Ed.). Springer, 299–313.
22. Alexander Keller. 2013. Quasi-Monte Carlo Image Synthesis in a Nutshell. In Monte Carlo and Quasi-Monte Carlo Methods 2012, Joseph Dick, Frances Kuo, Gareth Peters, and Ian Sloan (Eds.). Springer, 203–238.
23. Lauwerens Kuipers and Harald Niederreiter. 2012. Uniform distribution of sequences. Courier Corporation.
24. Pierre L’Ecuyer and David Munger. 2016. Lattice Builder: A General Software Tool for Constructing Rank-1 Lattice Rules. https://github.com/umontreal-simul/latnetbuilder.
25. Christiane Lemieux. 2009. Monte Carlo and Quasi Monte Carlo Sampling. Springer.
26. Hongli Liu, Honglei Han, and Min Jiang. 2021. Rank-1 Lattices for Efficient Path Integral Estimation. Computer Graphics Forum (2021).
27. Harald Niederreiter. 1992. Random Number Generation and quasi-Monte Carlo Methods. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, USA.
28. Victor Ostromoukhov, Charles Donohue, and Pierre-Marc Jodoin. 2004. Fast Hierarchical Importance Sampling with Blue Noise Properties. ACM Transactions on Graphics 23, 3 (2004), 488–495. Proc. SIGGRAPH 2004.
29. Art Owen. 1995. Randomly Permuted (t, m, s)-Nets and (t, s)-Sequences. In Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing (Lecture Notes in Statistics, Vol. 106), Harald Niederreiter and Peter Shiue (Eds.). Springer, 299–315.
30. Art Owen. 1998. Scrambling Sobol’ and Niederreiter-Xing Points. Journal of Complexity 14, 4 (1998), 466–489.
31. Lois Paulin, Nicolas Bonneel, David Coeurjolly, Jean-Claude Iehl, Antoine Webanck, Mathieu Desbrun, and Victor Ostromoukhov. 2020. Sliced optimal transport sampling. ACM Trans. Graph 39 (2020).
32. Hélène Perrier, David Coeurjolly, Feng Xie, Matt Pharr, Pat Hanrahan, and Victor Ostromoukhov. 2018. Sequences with Low-Discrepancy Blue-Noise 2-D Projections. In Computer Graphics Forum, Vol. 37. Wiley Online Library, 339–353.
33. Matt Pharr, Wenzel Jakob, and Greg Humphreys. 2016. Physically Based Rendering: From Theory to Implementation (3 ed.). Morgan-Kaufmann.
34. Bernhard Reinert, Tobias Ritschel, Hans-Peter Seidel, and Iliyan Georgiev. 2016. Projective blue-noise sampling. In Computer Graphics Forum, Vol. 35. Wiley Online Library, 285–295.
35. Gurprit Singh, Cengiz Öztireli, Abdalla GM Ahmed, David Coeurjolly, Kartic Subr, Oliver Deussen, Victor Ostromoukhov, Ravi Ramamoorthi, and Wojciech Jarosz. 2019. Analysis of sample correlations for Monte Carlo rendering. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 473–491.
36. Neil James Alexander Sloane. 2017. The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A058943 (2017).
37. Il’ya Meerovich Sobol’. 1967. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 7, 4 (1967), 784–802.
38. Yahan Zhou, Haibin Huang, Li-Yi Wei, and Rui Wang. 2012. Point sampling with general noise spectrum. ACM Trans. Graph. 31, 4 (2012), 76.