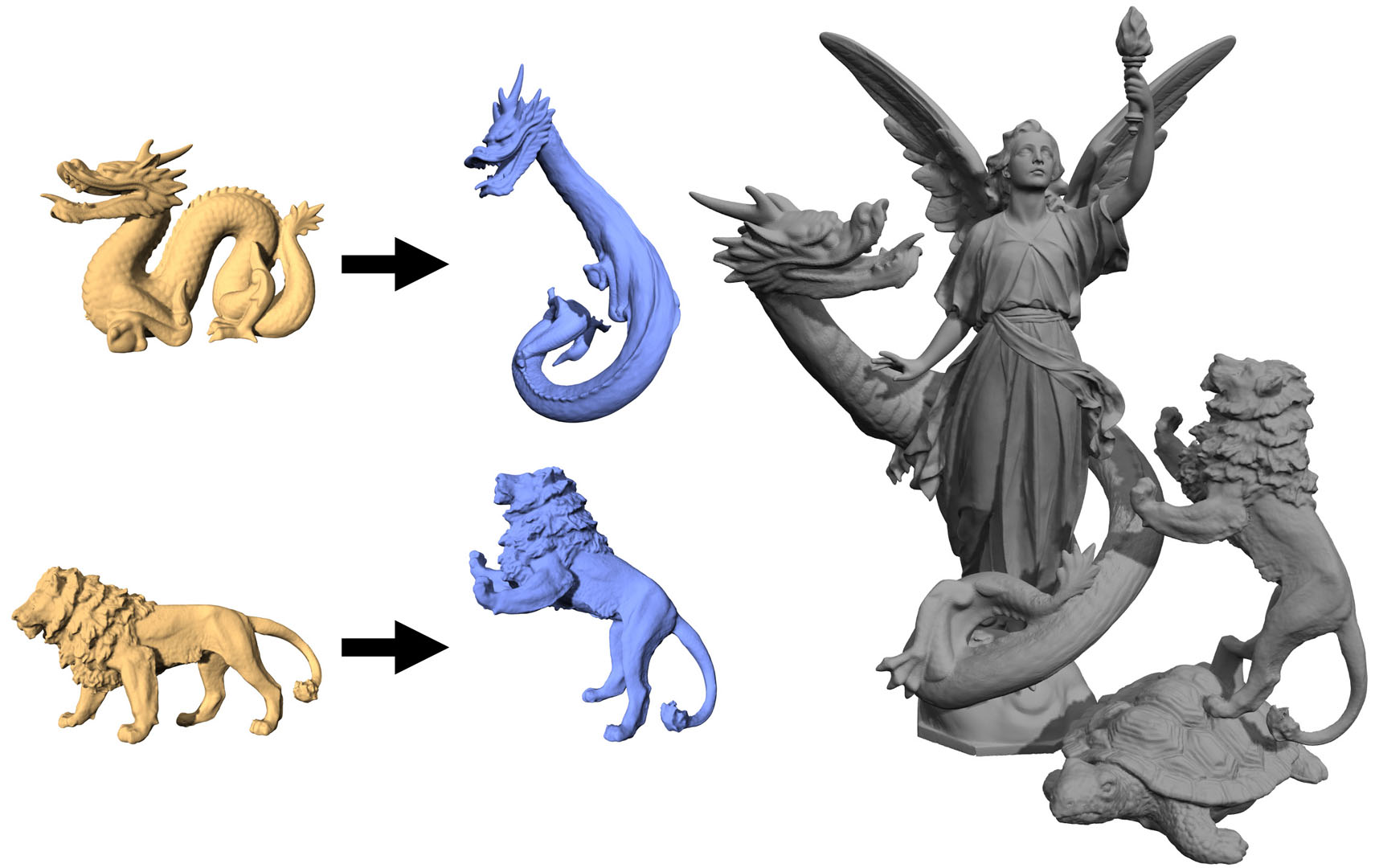
“A fast multigrid algorithm for mesh deformation” by Shi, Yu, Bell and Feng

In this paper, we present a multigrid technique for efficiently deforming large surface and volume meshes. We show that a previous least-squares formulation for distortion minimization reduces to a Laplacian system on a general graph structure for which we derive an analytic expression. We then describe an efficient multigrid algorithm for solving the relevant equations. Here we develop novel prolongation and restriction operators used in the multigrid cycles. Combined with a simple but effective graph coarsening strategy, our algorithm can outperform other multigrid solvers and the factorization stage of direct solvers in both time and memory costs for large meshes. It is demonstrated that our solver can trade off accuracy for speed to achieve greater interactivity, which is attractive for manipulating large meshes. Our multigrid solver is particularly well suited for a mesh editing environment which does not permit extensive precomputation. Experimental evidence of these advantages is provided on a number of meshes with a wide range of size. With our mesh deformation solver, we also successfully demonstrate that visually appealing mesh animations can be generated from both motion capture data and a single base mesh even when they are inconsistent.

1. Aksoylu, B., Khodakovsky, A., and Schröder, P. 2005. Multilevel solvers for unstructured surface meshes. SIAM Journal on Scientific Computing 26, 4, 1146–1165. Google ScholarDigital Library
2. Alexa, M., Cohen-Or, D., and Levin, D. 2000. As-rigid-as-possible shape interpolation. In SIGGRAPH 2000 Conference Proceedings, 157–164. Google ScholarDigital Library
3. Alexa, M. 2003. Differential coordinates for local mesh morphing and deformation. The Visual Computer 19, 2, 105–114.Google ScholarCross Ref
4. Bolz, J., Farmer, I., Grinspun, E., and Schröder, P. 2003. Sparse matrix solvers on the gpu: Conjugate gradients and multigrid. ACM Transactions on Graphics 22, 3, 917–924. Google ScholarDigital Library
5. Botsch, M., and Kobbelt, L. 2005. Real-time shape editing using radial basis functions. Computer Graphics Forum (Eurographics 2005) 24, 3, 611–621.Google Scholar
6. Botsch, M., Bommes, D., and Kobbelt, L. 2005. Efficient linear system solvers for mesh processing. In Proc. of IMA conference on Mathematics of Surfaces, 62–83. Google ScholarDigital Library
7. Clarenz, U., Griebel, M., Rumpf, M., Schweitzer, M., and Telea, A. 2004. Feature sensitive multiscale editing on surfaces. The Visual Computer 20, 329–343. Google ScholarDigital Library
8. Davis, T. A. 2005. Umfpack version 4.4 user guide. Tech. Rep. TR-04-003, University of Florida.Google Scholar
9. Davis, T. A. 2006. User guide for cholmod. Tech. rep., University of Florida.Google Scholar
10. Demmel, J., Eisenstat, S., Gilbert, J., Li, X., and Liu, J. 1999. A supernodal approach to sparse partial pivoting. SIAM Journal on Matrix Analysis and Applications 20, 3, 720–755. Google ScholarDigital Library
11. Goodnight, N., Woolley, C., Lewin, G., Luebke, D., and Humphreys, G. 2003. A multigrid solver for boundary value problems using programmable graphics hardware. In Graphics Hardware, 102–111. Google ScholarDigital Library
12. Gould, N. I. M., Hu, Y., and Scott, J. A. 2005. A numerical evaluation of sparse direct solvers for the solution of large sparse, symmetric linear systems of equations. Tech. Rep. RAL-TR-2005-005, RAL Technical Reports.Google Scholar
13. Grady, L., and Tasdizen, T. 2005. A geometric multigrid approach to solving the 2d inhomogeneous Laplace equation with internal Dirichlet boundary conditions. In International Conference on Image Processing.Google Scholar
14. Guskov, I., Sweldens, W., and Schröder, P. 1999. Multiresolution signal processing for meshes. In Proc. SIGGRAPH’99, 325–334. Google ScholarDigital Library
15. Heroux, M. A., and Willenbring, J. M. 2003. Trilinos users guide. Tech. Rep. SAND2003-2952, Sandia National Laboratories.Google Scholar
16. Kimmel, R., and Yavneh, I. 2003. An algebraic multigrid approach for image analysis. SIAM J. Sci. Comput. 24, 4, 1218–1231. Google ScholarDigital Library
17. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. In Proc. SIGGRAPH’98, 105–114. Google ScholarDigital Library
18. Lipman, Y., Sorkine, O., Levin, D., and Cohen-Or, D. 2005. Linear rotation-invariant coordinates for meshes. ACM Transactions on Graphics 24, 3. Google ScholarDigital Library
19. Ni, X., Garland, M., and Hart, J. 2004. Fair morse functions for extracting the topological structure of a surface mesh. ACM Transactions on Graphics 23, 3. Google ScholarDigital Library
20. Ray, N., and Levy, B. 2003. Hierarchical least squares conformal map. In Proceedings of Pacific Graphics, 263–270. Google ScholarDigital Library
21. Sederberg, T., and Parry, S. 1986. Free-form deformation of solid geometric models. Computer Graphics(SIGGRAPH’86) 20, 4, 151–160. Google ScholarDigital Library
22. Sorkine, O., Cohen-Or, D., Lipman, Y., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Symposium of Geometry Processing. Google ScholarDigital Library
23. Sumner, R., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Transactions on Graphics 23, 3, 397–403. Google ScholarDigital Library
24. Sumner, R., Zwicker, M., Gotsman, C., and Popović, J. 2005. Mesh-based inverse kinematics. ACM Transactions on Graphics 24, 3. Google ScholarDigital Library
25. Toledo, S., Rotkin, V., and Chen, D. 2003. Taucs:a library of sparse linear solvers. version 2.2. Tech. rep., Tel-Aviv University.Google Scholar
26. Trottenberg, U., Oosterlee, C., and Schuller, A. 2000. Multigrid. Academic Press. Google ScholarDigital Library
27. Wesseling, P. 2004. An Introduction to Multigrid Methods. R. T. Edwards, Inc.Google Scholar
28. Yu, Y., Zhou, K., Xu, D., Shi, X., Bao, H., Guo, B., and Shum, H.-Y. 2004. Mesh editing with poisson-based gradient field manipulation. ACM Transactions on Graphics (special issue for SIGGRAPH 2004) 23, 3, 641–648. Google ScholarDigital Library
29. Zayer, R., Rössl, C., Karni, Z., and Seidel, H.-P. 2005. Harmonic guidance for surface deformation. Computer Graphics Forum (Eurographics 2005) 24, 3.Google Scholar
30. Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B., and Shum, H.-Y. 2005. Large mesh deformation using the volumetric graph laplacian. ACM Transactions on Graphics 24, 3. Google ScholarDigital Library
31. Zorin, D., Schröder, P., and Sweldens, W. 1997. Interactive mutiresolution mesh editing. In SIGGRAPH 97 Proceedings, 259–268. Google ScholarDigital Library