“State of the Art in Grid-Free Monte Carlo Methods for Partial Differential Equations” by Sawhney, Miller, Gkioulekas and Crane
Conference:
Type(s):
Title:
- State of the Art in Grid-Free Monte Carlo Methods for Partial Differential Equations
Organizer(s):
Presenter(s)/Author(s):
Abstract:
This 3 hour course provides a detailed overview of grid-free Monte Carlo methods for solving partial differential equations (PDEs) based on the walk on spheres (WoS) algorithm, with a special emphasis on problems with high geometric complexity. PDEs are a basic building block for models and algorithms used throughout science, engineering and visual computing. Yet despite decades of research, conventional PDE solvers struggle to capture the immense geometric complexity of the natural world. A perennial challenge is spatial discretization: traditionally, one must partition the domain into a high-quality volumetric mesh—a process that can be brittle, memory intensive, and difficult to parallelize. WoS makes a radical departure from this approach, by reformulating the problem in terms of recursive integral equations that can be estimated via the Monte Carlo method, eliminating the need for spatial discretization. Since these equations strongly resemble those found in light transport theory, one can leverage deep knowledge from Monte Carlo rendering to develop new PDE solvers that share many of its advantages: no meshing, trivial parallelism, and the ability to evaluate the solution at any point without solving a global system of equations. The course is divided into two parts with a hands-on lab. Part I covers the basics of using WoS to solve fundamental PDEs like the Poisson equation. Topics include formulating the solution as an integral, generating samples via recursive random walks, and employing accelerated distance and ray intersection queries to efficiently handle complex geometries. Part II features a mini-panel of academic and industry contributors covering advanced topics including variance reduction, differentiable and multi-physics simulation, and applications to industrial design and robust geometry processing. Lab participants will gain experience setting up demo applications involving data interpolation, heat transfer, and geometric optimization using the open-source “Zombie” library, which implements various grid-free Monte Carlo PDE solvers.
Additional Information:
-
- Broad Applicability of PDEs
- Challenges with Conventional PDE Solvers
- Photorealistic Rendering: From Radiosity to Monte Carlo Ray Tracing
- Preview of Results
- Course Overview
-
- Estimation of Integrals: Numerical quadrature and aliasing
- Monte Carlo Estimation: Bias, Consistency, Variance
- Sample Generation
- Numerical and Computational Considerations
-
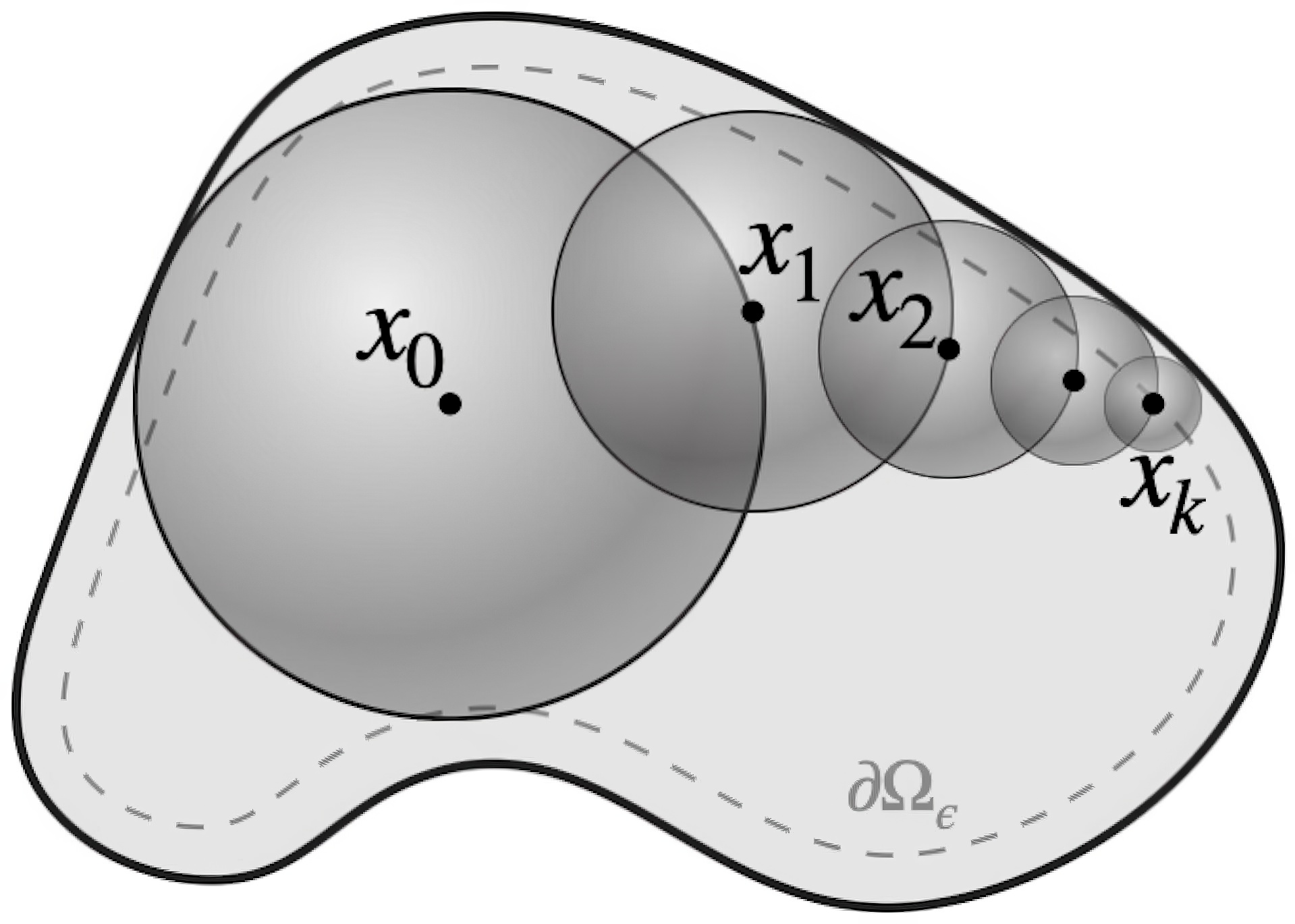
- Mean-Value Property of Harmonic Functions
- Recursive Monte Carlo Estimation
- Closest Point Queries
- Benefits of Monte Carlo
-
- Green’s Functions
- Importance Sampling
-
- Boundary Integral Equation
- Direction Sampling
- Random Walk on Star-Shaped Regions
- Closest Silhouette Point Queries
-
- Extension to Robin Boundary Conditions
- Extension to PDEs with Spatially Varying Material Coefficients
-
- Stress Tests on Complex Geometric Domains
- Comparisons to Grid-based PDE Solvers
- Current Limitations and Future Directions
-
- Bidirectional Schemes, Boundary and Mean Value Caching (Dario Seyb)
- Neural Caching and Control Variates (Guandao Yang)
- Kelvin Transform For Exterior Problems (Sina Nabizadeh)
-
- Differential Walk on Spheres for Shape Optimization (Zihan Yu)
- Differential Walk on Spheres for Material Coefficients (Ekrem Yilzamer)
-
- Stochastic Computation of Barycentric Coordinates (Fernando de Goes)
- Monte Carlo Fluid Simulation (Ryusuke Sugimoto)
- Coupling Conduction, Convection and Radiation for Infrared Imaging (Mégane Bati)
- Using Walk on Spheres for Injection Molding Design (Vojtech Molda)
Intermediate
Prerequisite: undergraduate calculus
Topics: DeNoise, Numerical Methods, Research, Sampling
List of topics and approximate times:
Part 1 (1 hour 35 minutes, 5 additional minutes of Q/A)
I – Motivation (15 minutes)
II – Basics of Monte Carlo Integration (10 minutes)
III – Walk on Spheres for Solving Laplace Equations (12 minutes)
IV – Walk on Spheres for Solving Poisson Equations (8 minutes)
V – Generalizing Walk on Spheres for Neumann Boundary Conditions (20 minutes)
VI – Walk on Spheres as a Technique For Simulating Brownian Motion (20 minutes)
VII – Evaluation (10 minutes)
Break: 5 minutes
Part 2 (1 hour 15 minutes, roughly 8 minutes per presentation)
I – Variance Reduction (25 minutes)
II – Differentiability (15 minutes)
III – Applications (35 minutes)
Additional Info: We describe grid-free Monte Carlo methods for solving partial differential equations on complex geometries. These methods offer unique opportunities to accelerate engineering design cycles by being easy to parallelize and output-sensitive like Monte Carlo rendering, while bypassing the need for simulation-ready meshes that are burdensome to generate for conventional solvers.