“Multiple-bounce Smith Microfacet BRDFs using the Invariance Principle” by Cui, Pan, Yang, Zhang, Yan, et al. …
Conference:
Type(s):
Title:
- Multiple-bounce Smith Microfacet BRDFs using the Invariance Principle
Session/Category Title: Materials
Presenter(s)/Author(s):
Abstract:
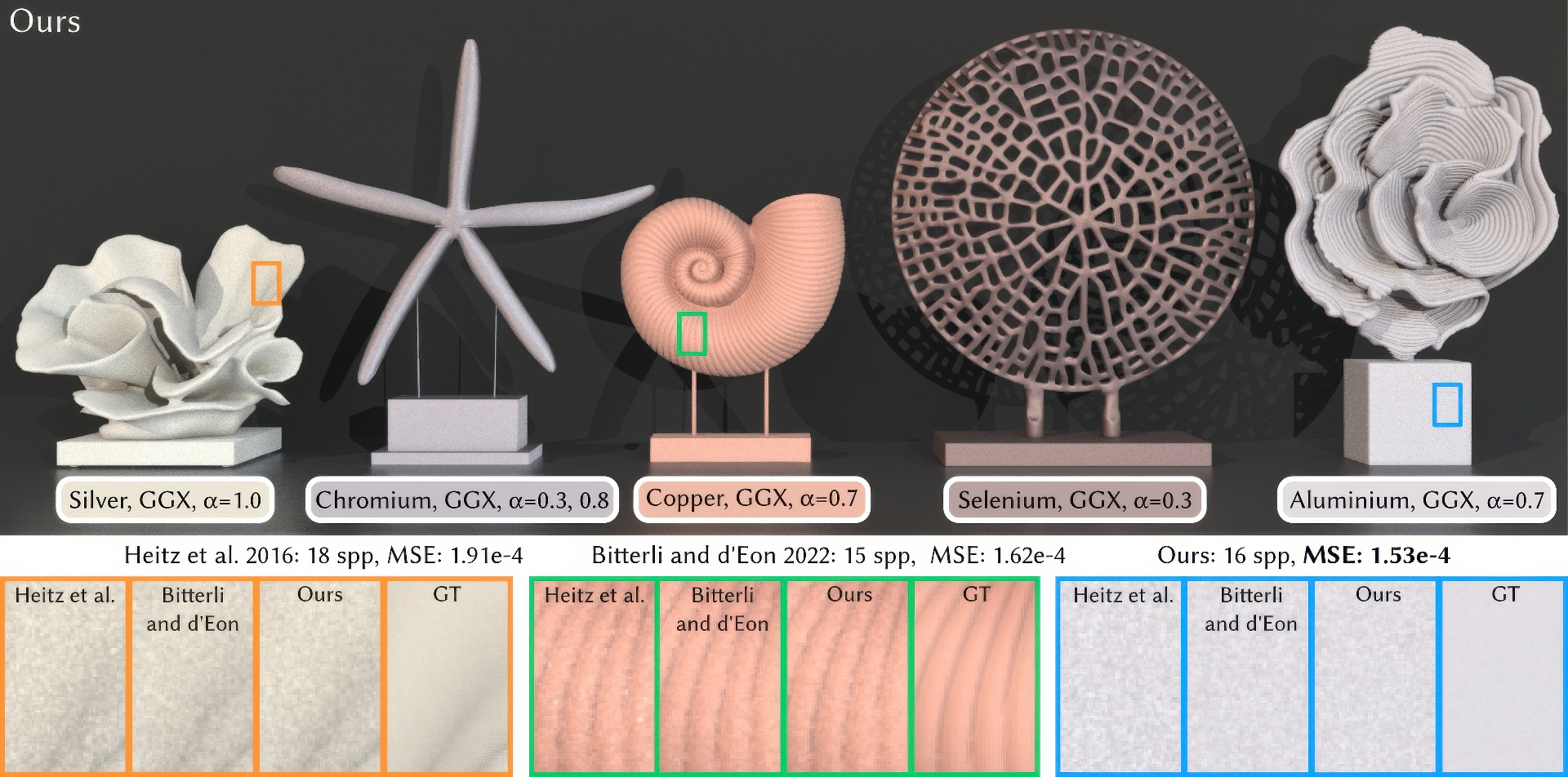
Smith microfacet models are widely used in computer graphics to represent materials. Traditional microfacet models do not consider the multiple bounces on microgeometries, leading to visible energy missing, especially on rough surfaces. Later, as the equivalence between the microfacets and volume has been revealed, random walk solutions have been proposed to introduce multiple bounces, but at the cost of high variance. Recently, the position-free property has been introduced into the multiple-bounce model, resulting in much less noise, but also bias or a complex derivation. In this paper, we propose a simple way to derive the multiple-bounce Smith microfacet bidirectional reflectance distribution functions (BRDFs) using the invariance principle. At the core of our model is a shadowing-masking function for a path consisting of direction collections, rather than separated bounces. Our model ensures unbiasedness and can produce less noise compared to the previous work with equal time, thanks to the simple formulation. Furthermore, we also propose a novel probability density function (PDF) for BRDF multiple importance sampling, which has a better match with the multiple-bounce BRDFs, producing less noise than previous naive approximations.
References:
[1]
V. A. Ambartsumian. 1943. The problem of diffuse reflection of light by a turbid medium. Dokl. Akad. Nauk SSSR 19 (1943), 30–41.
[2]
V. A. Ambartsumian. 1944. On the problem of diffuse reflection of light. Journal of Physics 8, 2 (1944), 65–75.
[3]
J. R. Arvo and D. S. Kirk. 1990. Particle transport and image synthesis. ACM SIGGRAPH Computer Graphics (1990).
[4]
Yaoyi Bai, Songyin Wu, Zheng Zeng, Beibei Wang, and Ling-Qi Yan. 2022. BSDF Importance Baking: A Lightweight Neural Solution to Importance Sampling Parametric BSDFs. https://doi.org/10.48550/ARXIV.2210.13681
[5]
P. Beckmann and A. Spizzichino. 1963. The scattering of electromagnetic waves from rough surfaces. Pergamon Press.
[6]
Benedikt Bitterli and Eugene d’Eon. 2022. A Position-Free Path Integral for Homogeneous Slabs and Multiple Scattering on Smith Microfacets. Computer Graphics Forum 41, 4 (2022), 93–104. https://doi.org/10.1111/cgf.14589
[7]
S. Chandrasekhar. 1960. Radiative Transfer. Dover.
[8]
Robert L. Cook and Kenneth E. Torrance. 1982. A Reflectance Model for Computer Graphics. ACM Trans. Graph. 1, 1 (Jan. 1982), 7–24.
[9]
Eugene d’Eon. 2021. An analytic BRDF for materials with spherical Lambertian scatterers. In Computer Graphics Forum, Vol. 40. Wiley Online Library, 153–161.
[10]
Jonathan Dupuy, Eric Heitz, and Eugene d’Eon. 2016. Additional Progress Towards the Unification of Microfacet and Microflake Theories. In EGSR – Experimental Ideas & Implementations. The Eurographics Association, 55–63.
[11]
V. Falster, A. Jarabo, and J. R. Frisvad. 2020. Computing the Bidirectional Scattering of a Microstructure Using Scalar Diffraction Theory and Path Tracing. Computer Graphics Forum 39, 7 (2020), 231–242.
[12]
Bruce Hapke. 1981. Bidirectional reflectance spectroscopy: 1. Theory. Journal of Geophysical Research: Solid Earth 86, B4 (1981), 3039–3054.
[13]
Eric Heitz. 2014. Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs. Journal of Computer Graphics Techniques (JCGT) 3, 2 (30 June 2014), 48–107. http://jcgt.org/published/0003/02/03/
[14]
Eric Heitz, Johannes Hanika, Eugene d’Eon, and Carsten Dachsbacher. 2016. Multiple-Scattering Microfacet BSDFs with the Smith Model. ACM Trans. Graph. 35, 4, Article 58 (July 2016), 14 pages.
[15]
Henry G. Horak and S. Chandrasekhar. 1961. Diffuse Reflection by a Semi-Infinite Atmosphere.The Astrophysical Journal 134 (July 1961), 45. https://doi.org/10.1086/147126
[16]
Wenzel Jakob. 2010. Mitsuba renderer. http://www.mitsuba-renderer.org.
[17]
Christopher Kulla and Alejandro Conty. 2017. Physically Based Shading in Theory and Practice – Revisiting Physically Based Shading at Imageworks. http://blog.selfshadow.com/publications/s2017-shading-course/.
[18]
Joo Lee, Adrián Jarabo, Daniel Jeon, Diego Gutiérrez, and Min Kim. 2018. Practical multiple scattering for rough surfaces. ACM Trans. Graph. 37, Article 175 (Dec. 2018), 12 pages.
[19]
Matt Pharr and Pat Hanrahan. 2000. Monte Carlo Evaluation of Non-Linear Scattering Equations for Subsurface Reflection. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. ACM Press/Addison-Wesley Publishing Co., USA, 75–84. https://doi.org/10.1145/344779.344824
[20]
Vincent Ross, Denis Dion, and Guy Potvin. 2005. Detailed analytical approach to the Gaussian surface bidirectional reflectance distribution function specular component applied to the sea surface. J. Opt. Soc. Am. A 22, 11 (Nov. 2005), 2442–2453.
[21]
Vincent Schüssler, Eric Heitz, Johannes Hanika, and Carsten Dachsbacher. 2017. Microfacet-Based Normal Mapping for Robust Monte Carlo Path Tracing. ACM Trans. Graph. 36, 6, Article 205 (2017), 12 pages.
[22]
B. Smith. 1967. Geometrical shadowing of a random rough surface. IEEE Transactions on Antennas and Propagation 15, 5 (1967), 668–671.
[23]
Emmanuel Turquin. 2019. Practical multiple scattering compensation for microfacet models. https://blog.selfshadow.com/publications/turquin/ms_comp_final.pdf.
[24]
Eric Veach. 1997. Robust Monte Carlo Methods for Light Transport Simulation. Ph.D. Dissertation. Stanford University.
[25]
Bruce Walter, Stephen R. Marschner, Hongsong Li, and Kenneth E. Torrance. 2007. Microfacet Models for Refraction through Rough Surfaces. In Rendering Techniques (proc. EGSR 2007). The Eurographics Association, 195–206.
[26]
Beibei Wang, Wenhua Jin, Jiahui Fan, Jian Yang, Nicolas Holzschuch, and Ling-Qi Yan. 2022a. Position-Free Multiple-Bounce Computations for Smith Microfacet BSDFs. ACM Trans. Graph. 41, 4, Article 134 (jul 2022), 14 pages.
[27]
Beibei Wang, Wenhua Jin, Miloš Hašan, and Ling-Qi Yan. 2022b. SpongeCake: A Layered Microflake Surface Appearance Model. ACM Trans. Graph. 42, 1, Article 8 (sep 2022), 16 pages. https://doi.org/10.1145/3546940
[28]
Feng Xie and Pat Hanrahan. 2018. Multiple Scattering from Distributions of Specular V-Grooves. ACM Trans. Graph. 37, 6, Article 276 (2018), 14 pages.
[29]
Feng Xie, Anton Kaplanyan, Warren Hunt, and Pat Hanrahan. 2019. Multiple Scattering Using Machine Learning. In ACM SIGGRAPH 2019 Talks. Article 70, 2 pages.