“A harmonic balance approach for designing compliant mechanical systems with nonlinear periodic motions” by Tang, Zehnder, Coros and Thomaszewski
Conference:
Type(s):
Title:
- A harmonic balance approach for designing compliant mechanical systems with nonlinear periodic motions
Session/Category Title: Computational Robotics
Presenter(s)/Author(s):
Abstract:
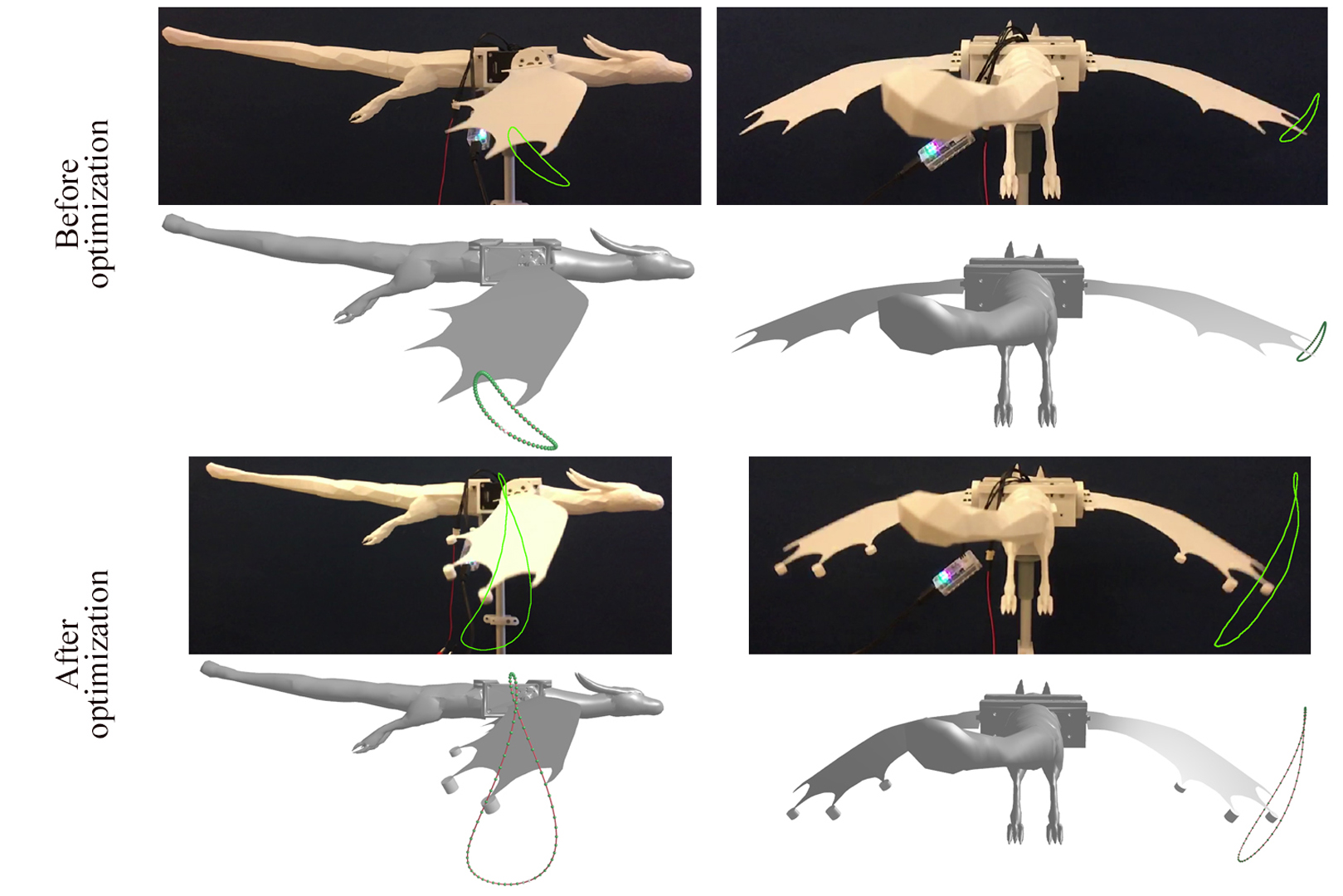
We present a computational method for designing compliant mechanical systems that exhibit large-amplitude oscillations. The technical core of our approach is an optimization-driven design tool that combines sensitivity analysis for optimization with the Harmonic Balance Method for simulation. By establishing dynamic force equilibrium in the frequency domain, our formulation avoids the major limitations of existing alternatives: it handles nonlinear forces, side-steps any transient process, and automatically produces periodic solutions. We introduce design objectives for amplitude optimization and trajectory matching that enable intuitive high-level authoring of large-amplitude motions. Our method can be applied to many types of mechanical systems, which we demonstrate through a set of examples involving compliant mechanisms, flexible rod networks, elastic thin shell models, and multi-material solids. We further validate our approach by manufacturing and evaluating several physical prototypes.
References:
1. Andrew Allen and Nikunj Raghuvanshi. 2015. Aerophones in Flatland: Interactive Wave Simulation of Wind Instruments. ACM Trans. Graph. 34, 4, Article 134 (July 2015), 11 pages. Google ScholarDigital Library
2. Moritz Bächer, Stelian Coros, and Bernhard Thomaszewski. 2015. LinkEdit: Interactive Linkage Editing Using Symbolic Kinematics. ACM Trans. Graph. 34, 4, Article 99 (July 2015), 8 pages. Google ScholarDigital Library
3. Moritz Bächer, Emily Whiting, Bernd Bickel, and Olga Sorkine-Hornung. 2014. Spin-It: Optimizing Moment of Inertia for Spinnable Objects. ACM Trans. Graph. 33, 4, Article 96 (July 2014), 10 pages. Google ScholarDigital Library
4. J. W. Bandler, R. M. Biernacki, and S. H. Chen. 1992. Harmonic balance simulation and optimization of nonlinear circuits. In [Proceedings] 1992 IEEE International Symposium on Circuits and Systems, Vol. 1. 85–88 vol.1. Google ScholarCross Ref
5. Jernej Barbič and Doug L. James. 2005. Real-Time Subspace Integration for St. Venant-Kirchhoff Deformable Models. ACM Trans. Graph. 24, 3 (July 2005), 982–990. Google ScholarDigital Library
6. Miklós Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, and Eitan Grinspun. 2008. Discrete Elastic Rods. In ACM SIGGRAPH 2008 Papers (Los Angeles, California) (SIGGRAPH ’08). Association for Computing Machinery, New York, NY, USA, Article 63, 12 pages. Google ScholarDigital Library
7. Gaurav Bharaj, David I. W. Levin, James Tompkin, Yun Fei, Hanspeter Pfister, Wojciech Matusik, and Changxi Zheng. 2015. Computational Design of Metallophone Contact Sounds. ACM Trans. Graph. 34, 6, Article 223 (Oct. 2015), 13 pages. Google ScholarDigital Library
8. Nicolas Bonneel, George Drettakis, Nicolas Tsingos, Isabelle Viaud-Delmon, and Doug James. 2008. Fast Modal Sounds with Scalable Frequency-Domain Synthesis. ACM Trans. Graph. 27, 3 (Aug. 2008), 1–9. Google ScholarDigital Library
9. Richard H Byrd, Peihuang Lu, Jorge Nocedal, and Ciyou Zhu. 1995. A limited memory algorithm for bound constrained optimization. SIAM Journal on scientific computing 16, 5 (1995), 1190–1208.Google Scholar
10. TM Cameron and JH Griffin. 1989. An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems. Journal of applied mechanics 56, 1 (1989), 149–154.Google ScholarCross Ref
11. Duygu Ceylan, Wilmot Li, Niloy J. Mitra, Maneesh Agrawala, and Mark Pauly. 2013. Designing and Fabricating Mechanical Automata from Mocap Sequences. ACM Trans. Graph. 32, 6, Article 186 (Nov. 2013), 11 pages. Google ScholarDigital Library
12. Jeffrey N Chadwick, Steven S An, and Doug L James. 2009. Harmonic shells: a practical nonlinear sound model for near-rigid thin shells. ACM Trans. Graph. 28, 5 (2009), 119–1.Google ScholarDigital Library
13. Desai Chen, David I. W. Levin, Wojciech Matusik, and Danny M. Kaufman. 2017. Dynamics-Aware Numerical Coarsening for Fabrication Design. ACM Trans. Graph. 36, 4, Article 84 (July 2017), 15 pages. Google ScholarDigital Library
14. Gabriel Cirio, Ante Qu, George Drettakis, Eitan Grinspun, and Changxi Zheng. 2018. Multi-scale simulation of nonlinear thin-shell sound with wave turbulence. ACM Transactions on Graphics (TOG) 37, 4 (2018), 110.Google ScholarDigital Library
15. Stelian Coros, Bernhard Thomaszewski, Gioacchino Noris, Shinjiro Sueda, Moira Forberg, Robert W. Sumner, Wojciech Matusik, and Bernd Bickel. 2013. Computational Design of Mechanical Characters. ACM Trans. Graph. 32, 4, Article 83 (July 2013), 12 pages. Google ScholarDigital Library
16. S. Cotton, I. M. C. Olaru, M. Bellman, T. van der Ven, J. Godowski, and J. Pratt. 2012. FastRunner: A fast, efficient and robust bipedal robot. Concept and planar simulation. In 2012 IEEE International Conference on Robotics and Automation. 2358–2364.Google Scholar
17. T. Detroux, L. Renson, and G. Kerschen. 2014. The Harmonic Balance Method for Advanced Analysis and Design of Nonlinear Mechanical Systems. In Nonlinear Dynamics, Volume 2, Gaetan Kerschen (Ed.). Springer International Publishing, Cham, 19–34.Google Scholar
18. Suguang Dou and Jakob Søndergaard Jensen. 2015. Optimization of nonlinear structural resonance using the incremental harmonic balance method. Journal of Sound and Vibration 334 (2015), 239–254. Google ScholarCross Ref
19. Anna Engels-Putzka, Jan Backhaus, and Christian Frey. 2019. Forced Response Sensitivity Analysis Using an Adjoint Harmonic Balance Solver. Journal of Turbomachinery 141, 3 (01 2019). Google ScholarCross Ref
20. Lawson Fulton, Vismay Modi, David Duvenaud, David I. W. Levin, and Alec Jacobson. 2019. Latent-space Dynamics for Reduced Deformable Simulation. Computer Graphics Forum (2019). Google ScholarCross Ref
21. Eitan Grinspun, Anil N Hirani, Mathieu Desbrun, and Peter Schröder. 2003. Discrete shells. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Eurographics Association, 62–67.Google ScholarDigital Library
22. Fabian Hahn, Bernhard Thomaszewski, Stelian Coros, Robert W. Sumner, Forrester Cole, Mark Meyer, Tony DeRose, and Markus Gross. 2014. Subspace Clothing Simulation Using Adaptive Bases. ACM Trans. Graph. 33, 4, Article 105 (July 2014), 9 pages. Google ScholarDigital Library
23. Kenneth C. Hall, Kivanc Ekici, Jeffrey P. Thomas, and Earl H. Dowell. 2013. Harmonic balance methods applied to computational fluid dynamics problems. International Journal of Computational Fluid Dynamics 27, 2 (2013), 52–67. arXiv:https://doi.org/10.1080/10618562.2012.742512 Google ScholarDigital Library
24. Klaus Hildebrandt, Christian Schulz, Christoph Von Tycowicz, and Konrad Polthier. 2011. Interactive Surface Modeling Using Modal Analysis. ACM Trans. Graph. 30, 5, Article 119 (Oct. 2011), 11 pages. Google ScholarDigital Library
25. Shayan Hoshyari, Hongyi Xu, Espen Knoop, Stelian Coros, and Moritz Bächer. 2019. Vibration-minimizing motion retargeting for robotic characters. ACM Transactions on Graphics (TOG) 38, 4 (2019), 1–14.Google ScholarDigital Library
26. Gaëtan Kerschen, Maxime Peeters, Jean-Claude Golinval, and Alexander F Vakakis. 2009. Nonlinear normal modes, Part I: A useful framework for the structural dynamicist. Mechanical Systems and Signal Processing 23, 1 (2009), 170–194.Google ScholarCross Ref
27. Theodore Kim and Doug L. James. 2009. Skipping Steps in Deformable Simulation with Online Model Reduction. ACM Trans. Graph. 28, 5 (Dec. 2009), 1–9. Google ScholarDigital Library
28. Malte Krack and Johann Gross. 2019. Harmonic Balance for Nonlinear Vibration Problems. Springer.Google Scholar
29. Malte Krack, Loic Salles, and Fabrice Thouverez. 2017. Vibration prediction of bladed disks coupled by friction joints. Archives of Computational Methods in Engineering 24, 3 (2017), 589–636.Google ScholarCross Ref
30. Dingzeyu Li, David I. W. Levin, Wojciech Matusik, and Changxi Zheng. 2016. Acoustic Voxels: Computational Optimization of Modular Acoustic Filters. ACM Trans. Graph. 35, 4, Article 88 (July 2016), 12 pages. Google ScholarDigital Library
31. Vittorio Megaro, Jonas Zehnder, Moritz Bächer, Stelian Coros, Markus H Gross, and Bernhard Thomaszewski. 2017. A computational design tool for compliant mechanisms. ACM Trans. Graph. 36, 4 (2017), 82–1.Google ScholarDigital Library
32. Federico L. Moro, Alexander Spröwitz, Alexandre Tuleu, Massimo Vespignani, Nikos G. Tsagarakis, Auke J. Ijspeert, and Darwin G. Caldwell. 2013. Horse-like walking, trotting, and galloping derived from kinematic Motion Primitives (kMPs) and their application to walk/trot transitions in a compliant quadruped robot. Biological Cybernetics 107, 3 (2013).Google Scholar
33. Simon Pabst, Sybille Krzywinski, Andrea Schenk, and Bernhard Thomaszewski. 2008. Seams and Bending in Cloth Simulation. In Workshop in Virtual Reality Interactions and Physical Simulation “VRIPHYS” (2008), Francois Faure and Matthias Teschner (Eds.). The Eurographics Association. Google ScholarCross Ref
34. Zherong Pan, Hujun Bao, and Jin Huang. 2015. Subspace Dynamic Simulation Using Rotation-Strain Coordinates. ACM Trans. Graph. 34, 6, Article 242 (Oct. 2015), 12 pages. Google ScholarDigital Library
35. Maxime Peeters, Régis Viguié, Guillaume Sérandour, Gaëtan Kerschen, and J-C Golinval. 2009. Nonlinear normal modes, Part II: Toward a practical computation using numerical continuation techniques. Mechanical systems and signal processing 23, 1 (2009), 195–216.Google Scholar
36. A. Pentland and J. Williams. 1989. Good Vibrations: Modal Dynamics for Graphics and Animation. In Proceedings of the 16th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’89). Association for Computing Machinery, New York, NY, USA, 215–222. Google ScholarDigital Library
37. Rüdiger Seydel. 2009. Practical bifurcation and stability analysis. Vol. 5. Springer Science & Business Media.Google Scholar
38. Ahmed A. Shabana. 1990. Theory of Vibration, Volume II: Discrete and Continuous Systems. Springer, New York, NY, USA.Google Scholar
39. Mélina Skouras, Bernhard Thomaszewski, Stelian Coros, Bernd Bickel, and Markus Gross. 2013. Computational Design of Actuated Deformable Characters. ACM Trans. Graph. 32, 4, Article 82 (July 2013), 10 pages. Google ScholarDigital Library
40. Mélina Skouras, Bernhard Thomaszewski, Peter Kaufmann, Akash Garg, Bernd Bickel, Eitan Grinspun, and Markus Gross. 2014. Designing Inflatable Structures. ACM Trans. Graph. (Proc. SIGGRAPH) 33, 4 (2014).Google ScholarDigital Library
41. Takuto Takahashi, Jonas Zehnder, Hiroshi G. Okuno, Shigeki Sugano, Stelian Coros, and Bernhard Thomaszewski. 2019. Computational Design of Statically Balanced Planar Spring Mechanisms. IEEE Robotics and Automation Letters 4 (2019), 4438–4444.Google ScholarCross Ref
42. Bernhard Thomaszewski, Stelian Coros, Damien Gauge, Vittorio Megaro, Eitan Grinspun, and Markus Gross. 2014. Computational Design of Linkage-Based Characters. ACM Trans. Graph. 33, 4, Article 64 (July 2014), 9 pages. Google ScholarDigital Library
43. Nobuyuki Umetani, Jun Mitani, Takeo Igarashi, and Kenshi Takayama. 2010. Designing Custommade Metallophone with Concurrent Eigenanalysis. In New Interfaces for Musical Expression++ (NIME++). 26–30.Google Scholar
44. Nobuyuki Umetani, Athina Panotopoulou, Ryan Schmidt, and Emily Whiting. 2016. Printone: Interactive Resonance Simulation for Free-Form Print-Wind Instrument Design. ACM Trans. Graph. 35, 6, Article 184 (Nov. 2016), 14 pages. Google ScholarDigital Library
45. Hongyi Xu, Espen Knoop, Stelian Coros, and Moritz Bächer. 2018. Bend-it: Design and Fabrication of Kinetic Wire Characters. ACM Trans. Graph. 37, 6, Article 239 (Dec. 2018), 15 pages. Google ScholarDigital Library
46. Jonas Zehnder, Stelian Coros, and Bernhard Thomaszewski. 2016. Designing Structurally-Sound Ornamental Curve Networks. ACM Trans. Graph. 35, 4, Article 99 (July 2016), 10 pages. Google ScholarDigital Library
47. Ran Zhang, Thomas Auzinger, Duygu Ceylan, Wilmot Li, and Bernd Bickel. 2017. Functionality-Aware Retargeting of Mechanisms to 3D Shapes. ACM Trans. Graph. 36, 4, Article 81 (July 2017), 13 pages. Google ScholarDigital Library
48. Changxi Zheng and Doug L. James. 2011. Toward High-Quality Modal Contact Sound. ACM Trans. Graph. 30, 4, Article 38 (July 2011), 12 pages. Google ScholarDigital Library