“Acoustic texture rendering for extended sources in complex scenes” by Zhang, Raghuvanshi, Snyder and Marschner – ACM SIGGRAPH HISTORY ARCHIVES

“Acoustic texture rendering for extended sources in complex scenes” by Zhang, Raghuvanshi, Snyder and Marschner

  • 2019 SA Technical Papers_Zhang_Acoustic texture rendering for extended sources in complex scenes

Conference:


Type(s):


Title:

    Acoustic texture rendering for extended sources in complex scenes

Session/Category Title:   Looking & Sounding Great

Presenter(s)/Author(s):


Moderator(s):


Abstract:


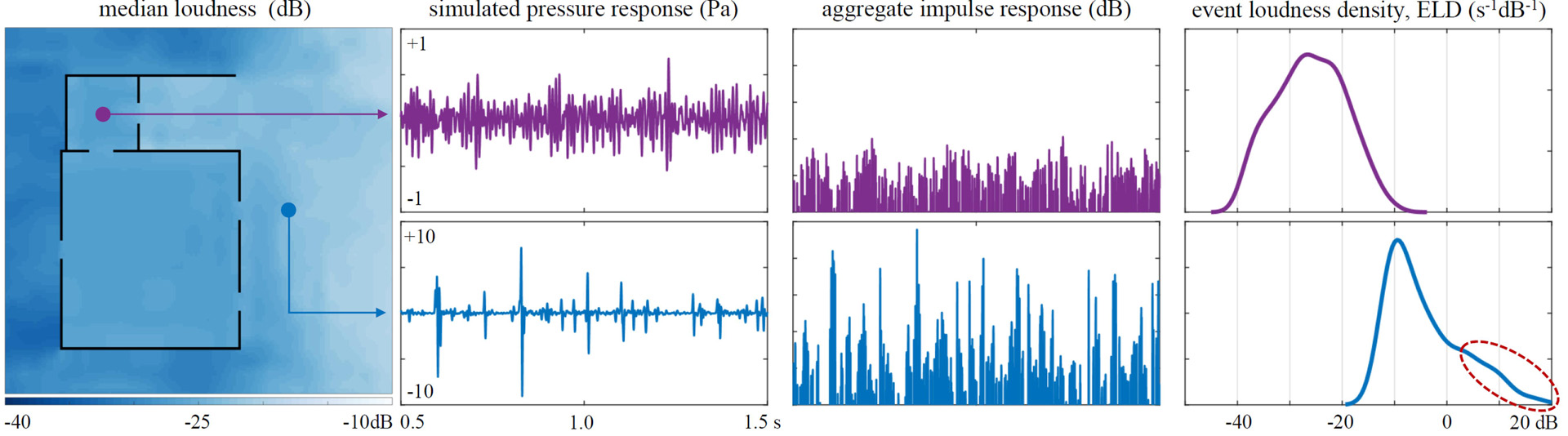
    Extended stochastic sources, like falling rain or a flowing waterway, provide an immersive ambience in virtual environments. In complex scenes, the rendered sound should vary naturally with listener position, differing not only in overall loudness but also in texture, to capture the indistinct murmur of a faraway brook versus the bright babbling of one up close. Modeling an ambient sound as a collection of random events such as individual raindrop impacts or water bubble oscillations, this variation can be seen as a change in the statistical distribution of events heard by the listener: the arrival rate of nearby, louder events relative to more distant or occluded, quieter ones. Reverberation and edge diffraction from scene geometry multiply and mix events more extensively compared to an empty scene and introduce salient spatial variation in texture. We formalize the notion of acoustic texture by introducing the event loudness density (ELD), which relates the rapidity of received events to their loudness. To model spatial variation in texture, the ELD is made a function of listener location in the scene. We show that this ELD field can be extracted from a single wave simulation for each extended source and rendered flexibly using a granular synthesis pipeline, with grains derived procedurally or from recordings. Our system yields believable, realtime changes in acoustic texture as the listener moves, driven by sound propagation in the scene.

References:


    1. Jean-Pierre Berenger. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of computational physics 114, 2 (1994), 185–200.Google ScholarDigital Library
    2. Marina Bosi and Richard E Goldberg. 2012. Introduction to digital audio coding and standards. Vol. 721. Springer Science & Business Media.Google Scholar
    3. Stephen Boyd, Neal Parikh, Eric Chu, Borja Peleato, Jonathan Eckstein, et al. 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning 3, 1 (2011), 1–122.Google Scholar
    4. Emmanuel J Candes, Justin K Romberg, and Terence Tao. 2006. Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences 59, 8 (2006), 1207–1223.Google Scholar
    5. Chunxiao Cao, Zhong Ren, Carl Schissler, Dinesh Manocha, and Kun Zhou. 2016. Interactive sound propagation with bidirectional path tracing. ACM Transactions on Graphics (TOG) 35, 6 (2016), 180.Google ScholarDigital Library
    6. Kees van den Doel. 2005. Physically based models for liquid sounds. ACM Transactions on Applied Perception (TAP) 2, 4 (2005), 534–546.Google ScholarDigital Library
    7. David L Donoho et al. 2006. Compressed sensing. IEEE Transactions on information theory 52, 4 (2006), 1289–1306.Google ScholarDigital Library
    8. Dennis Gabor. 1946. Theory of communication. Part 1: The analysis of information. Journal of the Institution of Electrical Engineers-Part III: Radio and Communication Engineering 93, 26 (1946), 429–441.Google ScholarCross Ref
    9. Brian Hamilton and Stefan Bilbao. 2017. FDTD Methods for 3-D Room Acoustics Simulation With High-Order Accuracy in Space and Time. IEEE/ACM Trans. Audio, Speech and Lang. Proc. 25, 11 (Nov. 2017), 2112–2124. Google ScholarDigital Library
    10. ISO 9613-1 1993. Acoustics – Attenuation of sound during propagation outdoors – Part 1: Calculation of the absorption of sound by the atmosphere. Standard. International Organization for Standardization, Geneva, CH.Google Scholar
    11. Timothy R. Langlois, Changxi Zheng, and Doug L. James. 2016. Toward Animating Water with Complex Acoustic Bubbles. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2016) 35, 4 (July 2016). Google ScholarDigital Library
    12. Shiguang Liu, Haonan Cheng, and Yiying Tong. 2019. Physically-based Statistical Simulation of Rain Sound. ACM Trans. Graph. 38, 4, Article 123 (July 2019), 14 pages. Google ScholarDigital Library
    13. J. H. McDermott, A. J. Oxenham, and E. P. Simoncelli. 2009. Sound texture synthesis via filter statistics. In 2009 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. 297–300. Google ScholarCross Ref
    14. Josh H. McDermott and Eero P. Simoncelli. 2011. Sound Texture Perception via Statistics of the Auditory Periphery: Evidence from Sound Synthesis. Neuron 71, 5 (2011), 926–940. Google ScholarCross Ref
    15. Stanley J Miklavcic, Andreas Zita, and Per Arvidsson. 2004. Computational real-time sound synthesis of rain. Department of Science and Technology (ITN), Campus Norrköping, Linköping.Google Scholar
    16. Nikunj Raghuvanshi and John Snyder. 2014. Parametric Wave Field Coding for Precomputed Sound Propagation. ACM Trans. Graph. 33, 4, Article 38 (July 2014), 11 pages. Google ScholarDigital Library
    17. Nikunj Raghuvanshi and John Snyder. 2018. Parametric Directional Coding for Precomputed Sound Propagation. ACM Trans. Graph. 37, 4, Article 108 (July 2018), 14 pages. Google ScholarDigital Library
    18. Nikunj Raghuvanshi, John Snyder, Ravish Mehra, Ming C. Lin, and Naga K. Govindaraju. 2010. Precomputed Wave Simulation for Real-Time Sound Propagation of Dynamic Sources in Complex Scenes. ACM Transactions on Graphics (proceedings of SIGGRAPH 2010) 29, 3 (July 2010).Google Scholar
    19. Curtis Roads. 2004. Microsound. MIT press.Google Scholar
    20. Lauri Savioja and U Peter Svensson. 2015. Overview of geometrical room acoustic modeling techniques. The Journal of the Acoustical Society of America 138, 2 (2015), 708–730.Google ScholarCross Ref
    21. Carl Schissler, Ravish Mehra, and Dinesh Manocha. 2014. High-order diffraction and diffuse reflections for interactive sound propagation in large environments. ACM Transactions on Graphics (TOG) 33, 4 (2014), 39.Google ScholarDigital Library
    22. Shtooka. 2010. Project Shtooka. http://shtooka.net/ Accessed: 2019-05-18.Google Scholar
    23. Allen Taflove and Susan C Hagness. 2005. Computational electrodynamics: the finite-difference time-domain method. Artech house.Google Scholar
    24. Robert Tibshirani. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) (1996), 267–288.Google Scholar
    25. Charles Verron, Mitsuko Aramaki, Richard Kronland-Martinet, and Grégory Pallone. 2009. A 3-D immersive synthesizer for environmental sounds. IEEE Transactions on Audio, Speech, and Language Processing 18, 6 (2009), 1550–1561.Google ScholarCross Ref
    26. Zechen Zhang, Nikunj Raghuvanshi, John Snyder, and Steve Marschner. 2018. Ambient Sound Propagation. ACM Trans. Graph. 6 (11 2018). Google ScholarDigital Library
    27. Andreas Zita. 2003. Computational Real-Time Sound Synthesis of Rain. Linköping University, Department of Science and Technology. 40 pages.Google Scholar

ACM Digital Library Publication:


Overview Page:


Submit a story:

If you would like to submit a story about this presentation, please contact us: historyarchives@siggraph.org