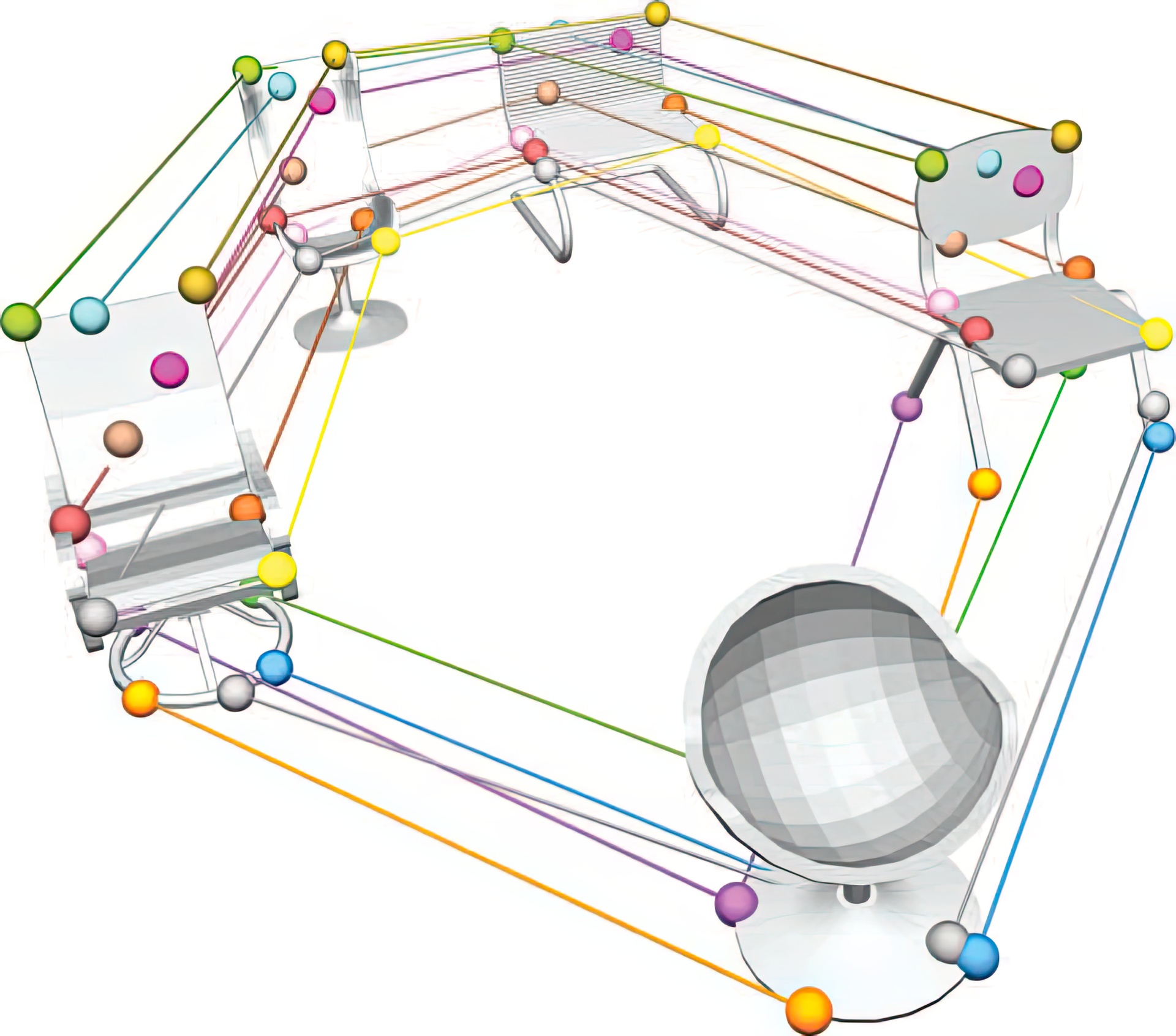
“An optimization approach for extracting and encoding consistent maps in a shape collection” by Huang, Zhang, Gao, Hu, Butscher, et al. … – ACM SIGGRAPH HISTORY ARCHIVES

“An optimization approach for extracting and encoding consistent maps in a shape collection” by Huang, Zhang, Gao, Hu, Butscher, et al. …

  • 2012 SA Technical Papers_Huang_An Optimization Approach for Extracting and Encoding Consistent Maps

Conference:


Type(s):


Title:

    An optimization approach for extracting and encoding consistent maps in a shape collection

Session/Category Title:   Shape Sets and Trees

Presenter(s)/Author(s):


Abstract:


    We introduce a novel approach for computing high quality point-to-point maps among a collection of related shapes. The proposed approach takes as input a sparse set of imperfect initial maps between pairs of shapes and builds a compact data structure which implicitly encodes an improved set of maps between all pairs of shapes. These maps align well with point correspondences selected from initial maps; they map neighboring points to neighboring points; and they provide cycle-consistency, so that map compositions along cycles approximate the identity map.The proposed approach is motivated by the fact that a complete set of maps between all pairs of shapes that admits nearly perfect cycle-consistency are highly redundant and can be represented by compositions of maps through a single base shape. In general, multiple base shapes are needed to adequately cover a diverse collection. Our algorithm sequentially extracts such a small collection of base shapes and creates correspondences from each of these base shapes to all other shapes. These correspondences are found by global optimization on candidate correspondences obtained by diffusing initial maps. These are then used to create a compact graphical data structure from which globally optimal cycle-consistent maps can be extracted using simple graph algorithms.Experimental results on benchmark datasets show that the proposed approach yields significantly better results than state-of-the-art data-driven shape matching methods.

References:


    1. Anguelov, D., Srinivasan, P., Pang, H.-C., Koller, D., Thrun, S., and Davis, J. 2004. The correlated correspondence algorithm for unsupervised registration of nonrigid surfaces. NIPS 17, 33–40.
    2. Chaudhuri, S., Kalogerakis, E., Guibas, L., and Koltun, V. 2011. Probabilistic reasoning for assembly-based 3d modeling. ACM Trans. Graph. 30, 4 (Aug.), 35:1–35:10.
    3. Cho, T. S., Avidan, S., and Freeman, W. T. 2010. A probabilistic image jigsaw puzzle solver. In CVPR, 183–190.
    4. Chui, H., and Rangarajan, A. 2003. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Underst. 89, 2–3 (Feb.), 114–141.
    5. Fisher, M., Savva, M., and Hanrahan, P. 2011. Characterizing structural relationships in scenes using graph kernels. ACM Trans. Graph. 30, 4 (Aug.), 34:1–34:12.
    6. Funkhouser, T., Kazhdan, M., Shilane, P., Min, P., Kiefer, W., Tal, A., Rusinkiewicz, S., and Dobkin, D. 2004. Modeling by example. ACM Trans. Graph. 23, 3 (Aug.), 652–663.
    7. Giorgi, D., Biasotti, S., and Paraboschi, L., 2007. Shape retrieval contest 2007: Watertight models track.
    8. Goldberg, D., Malon, C., and Bern, M. 2004. A global approach to automatic solution of jigsaw puzzles. Comput. Geom. Theory Appl. 28 (June), 165–174.
    9. Golovinskiy, A., and Funkhouser, T. A. 2009. Consistent segmentation of 3d models. Computers & Graphics 33, 3, 262–269.
    10. Huang, Q.-X., Flöry, S., Gelfand, N., Hofer, M., and Pottmann, H. 2006. Reassembling fractured objects by geometric matching. ACM Trans. Graph. 25, 3, 569–578.
    11. Huang, Q., Koltun, V., and Guibas, L. 2011. Joint shape segmentation using linear programming. ACM Trans. Graph. 30, 6 (Dec.), 125:1–125:12.
    12. Huber, D. 2002. Automatic Three-dimensional Modeling from Reality. PhD thesis, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA.
    13. James, D. L., and Twigg, C. D. 2005. Skinning mesh animations. ACM Trans. Graph. 24, 3 (July), 399–407.
    14. Kalogerakis, E., Hertzmann, A., and Singh, K. 2010. Learning 3d mesh segmentation and labeling. ACM Trans. Graph. 29 (July), 102:1–102:12.
    15. Kim, V. G., Lipman, Y., and Funkhouser, T. 2011. Blended intrinsic maps. ACM Trans. Graph. 30, 4 (Aug.), 79:1–79:12.
    16. Kim, V. G., Li, W., Mitra, N., DiVerdi, S., and Funkhouser, T. 2012. Exploring collections of 3d models using fuzzy correspondences. In ACM SIGGRAPH 2012 papers, SIGGRAPH ’12, to appear.
    17. Kumar, M. P., Kolmogorov, V., and Torr, P. H. S. 2009. An analysis of convex relaxations for MAP estimation of discrete MRFs. Journal of Machine Learning Research 10, 71–106.
    18. Leordeanu, M., and Hebert, M. 2006. Efficient map approximation for dense energy functions. ICML ’06, 545–552.
    19. Lipman, Y., and Funkhouser, T. 2009. Mobius voting for surface correspondence. ACM Trans. Graph. 28, 3 (July), 72:1–72:12.
    20. Marande, W., and Burger, G. 2007. Mitochondrial dna as a genomic jigsaw puzzle. Science 318 (October), 415.
    21. Mémoli, F., and Sapiro, G. 2005. A theoretical and computational framework for isometry invariant recognition of point cloud data. Foundations of Computational Mathematics 5, 3, 313–347.
    22. Nguyen, A., Ben-Chen, M., Welnicka, K., Ye, Y., and Guibas, L. 2011. An optimization approach to improving collections of shape maps. SGP ’11, 1481–1491.
    23. Ovsjanikov, M., Ben-Chen, M., Solomon, J., Butscher, A., and Guibas, L. 2012. Functional maps: A flexible representation of maps between shapes. ACM Transactions on Graphics 31, 4.
    24. Roberts, R., Sinha, S. N., Szeliski, R., and Steedly, D. 2011. Structure from motion for scenes with large duplicate structures. In CVPR, 3137–3144.
    25. Rubner, Y., Tomasi, C., and Guibas, L. J. 2000. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vision 40, 2 (Nov), 99–121.
    26. Sidi, O., va n Kaick, O., Kleiman, Y., Zhang, H., and Cohen-Or, D. 2011. Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering. ACM Trans. Graph. 30, 6 (Dec.), 126:1–126:10.
    27. Solomon, J., Nguyen, A., Butscher, A., Ben-Chen, M., and Guibas, L. 2012. Soft maps between surfaces. Computer Graphics Forum 31, 5, 1617–1626.
    28. Sumner, R. W., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Trans. Graph. 23, 3 (Aug.), 399–405.
    29. Sun, J., Ovsjanikov, M., and Guibas, L. 2009. A concise and provably informative multi-scale signature based on heat diffusion. Symposium on Geometry Processing ’09, 1383–1392.
    30. van Kaick, O., Tagliasacchi, A., Sidi, O., Zhang, H., Cohen-Or, D., Wolf, L., and Hamarneh, G. 2011. Prior knowledge for shape correspondence. Computer Graphics Forum 30, 2, 553–562.
    31. Zach, C., Klopschitz, M., and Pollefeys, M. 2010. Disambiguating visual relations using loop constraints. In CVPR, 1426–1433.

ACM Digital Library Publication:


Overview Page:


Submit a story:

If you would like to submit a story about this presentation, please contact us: historyarchives@siggraph.org