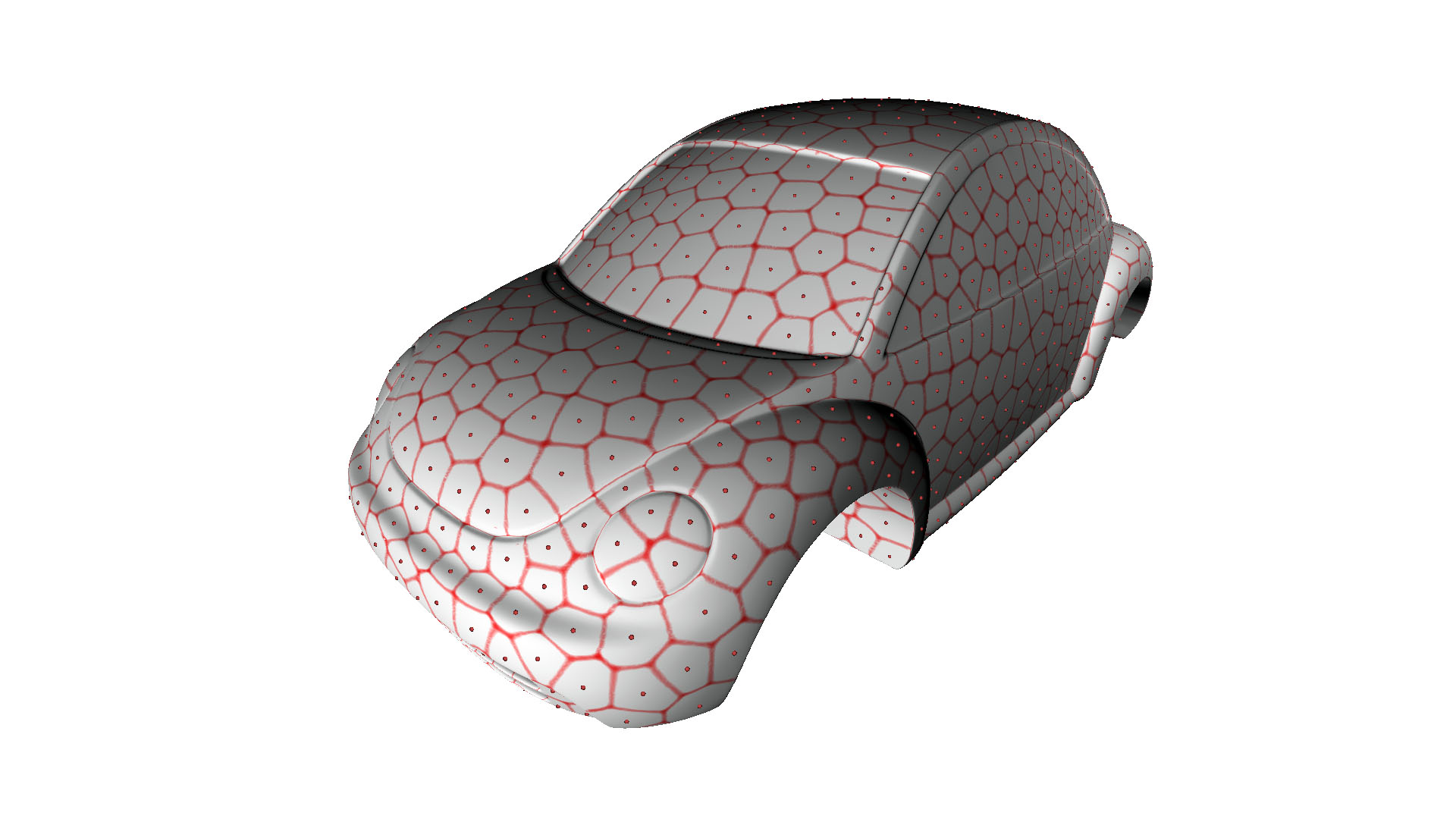
“Layered fields for natural tessellations on surfaces”
Conference:
Type(s):
Title:
- Layered fields for natural tessellations on surfaces
Session/Category Title:
- Meshing
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Mimicking natural tessellation patterns is a fascinating multi-disciplinary problem. Geometric methods aiming at reproducing such partitions on surface meshes are commonly based on the Voronoi model and its variants, and are often faced with challenging issues such as metric estimation, geometric, topological complications, and most critically, parallelization. In this paper, we introduce an alternate model which may be of value for resolving these issues. We drop the assumption that regions need to be separated by lines. Instead, we regard region boundaries as narrow bands and we model the partition as a set of smooth functions layered over the surface. Given an initial set of seeds or regions, the partition emerges as the solution of a time dependent set of partial differential equations describing concurrently evolving fronts on the surface. Our solution does not require geodesic estimation, elaborate numerical solvers, or complicated bookkeeping data structures. The cost per time-iteration is dominated by the multiplication and addition of two sparse matrices. Extension of our approach in a Lloyd’s algorithm fashion can be easily achieved and the extraction of the dual mesh can be conveniently preformed in parallel through matrix algebra. As our approach relies mainly on basic linear algebra kernels, it lends itself to efficient implementation on modern graphics hardware.
References:
1. Pierre Alliez, Éric Colin de Verdière, Olivier Devillers, and Martin Isenburg. 2003. Isotropic Surface Remeshing. In Proceedings of SMI ’03. 49–58. Google ScholarDigital Library
2. Keenan Crane, Clarisse Weischedel, and Max Wardetzky. 2013. Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow. ACM Trans. Graph. 32, 5, Article 152 (Oct. 2013), 11 pages. Google ScholarDigital Library
3. Qiang Du and Maria Emelianenko. 2006. Acceleration schemes for computing centroidal Voronoi tessellations. Num. Lin. Alg. with App. 13, 2–3 (2006), 173–192.Google ScholarCross Ref
4. Qiang Du, Max D. Gunzburger, and Lili Ju. 2003. Constrained Centroidal Voronoi Tessellations for Surfaces. SIAM J. on Sc. Comp. 24, 5 (2003), 1488–1506. Google ScholarDigital Library
5. G. J. Fix. 1981. Phase field methods for free boundary problems. In Proceedings of Interdisciplinary Symposium on Free Boundary Problems: Theory and Applications (Research Notes in Mathematics), Vol. 78, 79. 580–589.Google Scholar
6. A. Gersho. 1979. Asymptotically optimal block quantization. IEEE Transactions on Information Theory 25, 4 (Jul 1979), 373–380. Google ScholarDigital Library
7. Philipp Herholz, Felix Haase, and Marc Alexa. 2017. Diffusion Diagrams: Voronoi Cells and Centroids from Diffusion. Computer Graphics Forum (2017). Google ScholarDigital Library
8. Masao Iri, Kazuo Murota, and Takao Ohya. 1984. A fast Voronoi-diagram algorithm with applications to geographical optimization problems. Springer, 273–288.Google Scholar
9. Lili Ju, Qiang Du, and Max Gunzburger. 2002. Probabilistic methods for centroidal Voronoi tessellations and their parallel implementations. Parallel Comput. 28, 10 (2002), 1477 — 1500. Google ScholarDigital Library
10. R. Kimmel and J. A. Sethian. 1998. Computing Geodesic Paths on Manifolds. In Proc. Natl. Acad. Sci. USA. 8431–8435.Google Scholar
11. Randall J. LeVeque. 2002. Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
12. Yang Liu, Wenping Wang, Bruno Lévy, Feng Sun, Dong-Ming Yan, Lin Lu, and Chenglei Yang. 2009. On Centroidal Voronoi Tessellation—Energy Smoothness and Fast Computation. ACM Trans. Graph. 28, 4, Article 101 (Sept. 2009), 17 pages. Google ScholarDigital Library
13. S. Lloyd. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2 (Mar 1982), 129–137. Google ScholarDigital Library
14. J. MacQueen. 1967. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. Berkeley, Calif., 281–297.Google Scholar
15. NVIDIA. 2016. The API reference guide for cuSPARSE, the CUDA sparse matrix library. (v8.0 ed.). NVIDIA.Google Scholar
16. Atsuyuki Okabe, Barry Boots, and Kokichi Sugihara. 1992. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. John Wiley & Sons, Inc., New York, NY, USA. Google ScholarDigital Library
17. Gabriel Peyré and Laurent D. Cohen. 2006. Geodesic Remeshing Using Front Propagation. International Journal of Computer Vision 69, 1 (2006), 145. Google ScholarDigital Library
18. Yipeng Qin, Xiaoguang Han, Hongchuan Yu, Yizhou Yu, and Jianjun Zhang. 2016. Fast and Exact Discrete Geodesic Computation Based on Triangle-oriented Wavefront Propagation. ACM Trans. Graph. 35, 4, Article 125 (July 2016), 13 pages. Google ScholarDigital Library
19. Yipeng Qin, Hongchuan Yu, and Jianjun Zhang. 2017. Fast and Memory-Efficient Voronoi Diagram Construction on Triangle Meshes. Comput. Graph. Forum 36, 5 (Aug. 2017), 93–104. Google ScholarDigital Library
20. Robert J. Renka. 1997. Algorithm 772: STRIPACK: Delaunay Triangulation and Voronoi Diagram on the Surface of a Sphere. ACM Trans. Math. Softw. 23, 3 (1997), 416–434. Google ScholarDigital Library
21. Oliver Schall, Rhaleb Zayer, and Hans-Peter Seidel. 2008. Controlled field generation for quad-remeshing. In Proceedings of the 2008 ACM Symposium on Solid and Physical Modeling, Stony Brook, New York, USA, June 2–4, 2008. 295–300. Google ScholarDigital Library
22. S. Sengupta, M. Harris, Y. Zhang, and J. D. Owens. 2007. Scan Primitives for GPU Computing. In Proc. GH ’07. 97–106. Google ScholarDigital Library
23. J A Sethian. 1996. A fast marching level set method for monotonically advancing fronts. Proceedings of the National Academy of Sciences 93, 4 (1996), 1591–1595.Google ScholarCross Ref
24. Ingo Steinbach. 2000. Ein Multi-Phasen-Feld-Modell für facettiertes Kristallwachstum. Ph.D. Dissertation. Aachen, Techn. Hochsch., Diss., 2000.Google Scholar
25. Vitaly Surazhsky, Pierre Alliez, and Craig Gotsman. 2003. Isotropic remeshing of surfaces: a local parameterization approach. In Proc. 12th Int. Meshing Roundtable. 215–224.Google Scholar
26. Vitaly Surazhsky, Tatiana Surazhsky, Danil Kirsanov, Steven J. Gortler, and Hugues Hoppe. 2005. Fast Exact and Approximate Geodesics on Meshes. ACM Trans. Graph. 24, 3 (July 2005), 553–560. Google ScholarDigital Library
27. Greg Turk. 1991. Generating Textures on Arbitrary Surfaces Using Reaction-diffusion. In Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’91). ACM, New York, NY, USA, 289–298. Google ScholarDigital Library
28. Greg Turk. 1992. Re-tiling Polygonal Surfaces. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’92). ACM, New York, NY, USA, 55–64. Google ScholarDigital Library
29. Xiaoning Wang, Xiang Ying, Yong-Jin Liu, Shi-Qing Xin, Wenping Wang, Xianfeng Gu, Wolfgang Mueller-Wittig, and Ying He. 2015. Intrinsic computation of centroidal Voronoi tessellation (CVT) on meshes. Computer-Aided Design 58 (2015), 51 — 61. Google ScholarDigital Library
30. Andrew P. Witkin and Paul S. Heckbert. 1994. Using Particles to Sample and Control Implicit Surfaces. In Proc. SIGGRAPH ’94. ACM, New York, NY, USA, 269–277. Google ScholarDigital Library
31. Shi-Qing Xin, Bruno Lévy, Zhonggui Chen, Lei Chu, Yaohui Yu, Changhe Tu, and Wenping Wang. 2016. Centroidal Power Diagrams with Capacity Constraints: Computation, Applications, and Extension. ACM Trans. Graph. 35, 6 (Nov. 2016), 244:1–244:12. Google ScholarDigital Library
32. Xiang Ying, Xiaoning Wang, and Ying He. 2013. Saddle Vertex Graph (SVG): A Novel Solution to the Discrete Geodesic Problem. ACM Trans. Graph. 32, 6 (Nov. 2013), 12. Google ScholarDigital Library
33. Rhaleb Zayer, Markus Steinberger, and Hans-Peter Seidel. 2017. A GPU-Adapted Structure for Unstructured Grids. Computer Graphics Forum 36, 2 (2017), 495–507. Google ScholarDigital Library