“Delaunay mesh simplification with differential evolution”
Conference:
Type(s):
Title:
- Delaunay mesh simplification with differential evolution
Session/Category Title: Meshing
Presenter(s)/Author(s):
Moderator(s):
Abstract:
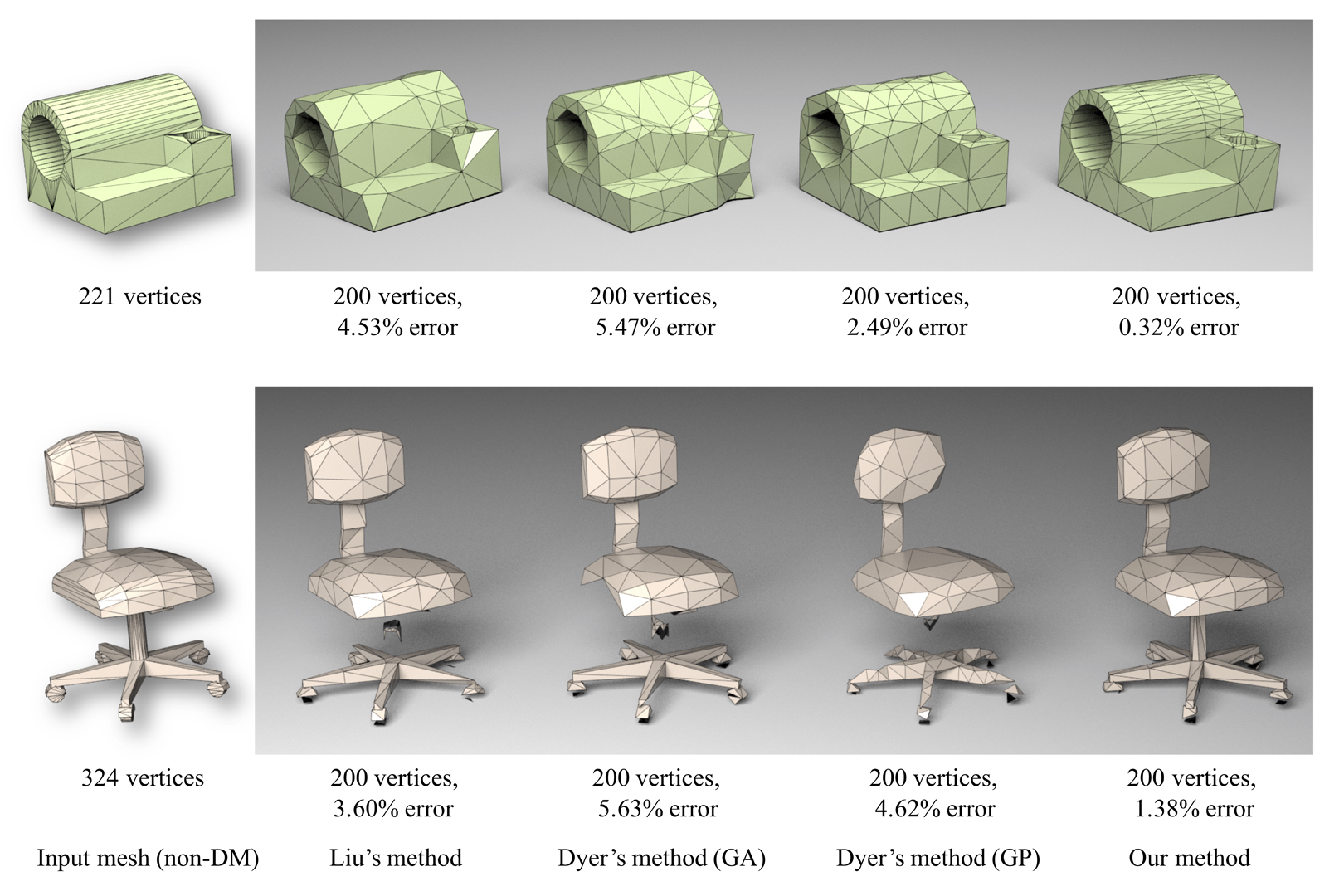
Delaunay meshes (DM) are a special type of manifold triangle meshes — where the local Delaunay condition holds everywhere — and find important applications in digital geometry processing. This paper addresses the general DM simplification problem: given an arbitrary manifold triangle mesh M with n vertices and the user-specified resolution m (< n), compute a Delaunay mesh M* with m vertices that has the least Hausdorffdistance to M. To solve the problem, we abstract the simplification process using a 2D Cartesian grid model, in which each grid point corresponds to triangle meshes with a certain number of vertices and a simplification process is a monotonic path on the grid. We develop a novel differential-evolution-based method to compute a low-cost path, which leads to a high quality Delaunay mesh. Extensive evaluation shows that our method consistently outperforms the existing methods in terms of approximation error. In particular, our method is highly effective for small-scale CAD models and man-made objects with sharp features but less details. Moreover, our method is fully automatic and can preserve sharp features well and deal with models with multiple components, whereas the existing methods often fail.
References:
1. Alexander I. Bobenko and Boris A. Springborn. 2007. A discrete Laplace-Beltrami operator for simplicial surfaces. Discrete & Computational Geometry 38, 4 (2007), 740–756. Jean-Daniel Boissonnat, Ramsay Dyer, and Arijit Ghosh. 2013. Constructing Intrinsic Delaunay Triangulations of Submanifolds. CoRR abs/1303.6493 (2013). Google ScholarDigital Library
2. Paolo Cignoni, Claudio Montani, and Roberto Scopigno. 1998a. A comparison of mesh simplification algorithms. Computers & Graphics 22, 1 (1998), 37–54.Google ScholarCross Ref
3. P Cignoni, C Rocchini, and R Scopigno. 1998b. Metro: Measuring Error on Simplified Surfaces. Computer Graphics Forum 17, 2 (1998), 167–174.Google Scholar
4. Swagatam Das, Sankha Subhra Mullick, and Ponnuthurai Nagartnam Suganthan. 2016. Recent advances in differential evolution – An updated survey. Swarm and Evolutionary Computation 27 (2016), 1–30.Google ScholarCross Ref
5. Swagatam Das and Ponnuthurai Nagartnam Suganthan. 2011. Differential Evolution: A Survey of the State-of-the-Art. IEEE Transactions on Evolutionary Computation 15, 1 (2011), 4–31. Google ScholarDigital Library
6. Ramsay Dyer, Hao Zhang, and Torsten Möller. 2007a. Delaunay Mesh Construction. In Proceedings of the Fifth Eurographics Symposium on Geometry Processing (SGP ’07). 273–282. Google ScholarDigital Library
7. Ramsay Dyer, Hao Zhang, and Torsten Möller. 2007b. Voronoi-Delaunay Duality and Delaunay Meshes. In Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling (SPM ’07). 415–420. Google ScholarDigital Library
8. Ramsay Dyer, Hao Zhang, and Torsten Möller. 2008. Surface Sampling and the Intrinsic Voronoi Diagram. In Proceedings of the Symposium on Geometry Processing (SGP ’08). 1393–1402. Google ScholarDigital Library
9. Herbert Edelsbrunner and Nimish R. Shah. 1997. Triangulating topological spaces. International Journal of Computational Geometry and Applications 7, 4 (1997), 365–378.Google ScholarCross Ref
10. Matthew Fisher, Boris Springborn, Peter Schröder, and Alexander I. Bobenko. 2007. An Algorithm for the Construction of Intrinsic Delaunay Triangulations with Applications to Digital Geometry Processing. Computing 81, 2–3 (Nov. 2007), 199–213. Google ScholarDigital Library
11. Michael Garland and Paul S. Heckbert. 1997. Surface Simplification Using Quadric Error Metrics. In ACM SIGGRAPH ’97. 209–216. Google ScholarDigital Library
12. Sayan Ghosh, Swagatam Das, Athanasios V. Vasilakos, and Kaushik Suresh. 2012. On Convergence of Differential Evolution Over a Class of Continuous Functions With Unique Global Optimum. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics 42, 1 (2012), 107–124. Google ScholarDigital Library
13. Paul S. Heckbert and Michael Garland. 1999. Optimal triangulation and quadric-based surface simplification. Computational Geometry: Theory and Applications 14, 1–3 (1999), 49–65. Google ScholarDigital Library
14. Hugues Hoppe. 1996. Progressive Meshes. In Proceedings of SIGGRAPH ’96. 99–108. Google ScholarDigital Library
15. Hugues Hoppe, Tony DeRose, Tom Duchamp, John McDonald, and Werner Stuetzle. 1993. Mesh Optimization. In SIGGRAPH ’93. 19–26. Google ScholarDigital Library
16. Reiner Horst, Panos M. Pardalos, and Nguyen Van Thoai. 2000. Introduction to Global Optimization. 2nd edition, Kluwer Academic Publishers. Google ScholarDigital Library
17. Kaimo Hu, Dong-Ming Yan, David Bommes, Pierre Alliez, and Bedrich Benes. 2017. Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement. IEEE Trans. Vis. Comput. Graph. 23, 12 (2017), 2560–2573.Google ScholarCross Ref
18. Jouni Lampinen and Ivan Zelinka. 1999. Mixed integer-discrete-continuous optimization with differential evolution. In Proc. 5th Int. Mendel Conf. Soft Comput. 71–76.Google Scholar
19. Bruno Lévy and Yang Liu. 2010. Lp Centroidal Voronoi Tessellation and Its Applications. ACM Trans. Graph. 29, 4, Article 119 (2010), 119:1–119:11 pages. Google ScholarDigital Library
20. Yong-Jin Liu, Dian Fan, Chun-Xu Xu, and Ying He. 2017. Constructing Intrinsic Delaunay Triangulations from the Dual of Geodesic Voronoi Diagrams. ACM Trans. Graph. 36, 2, Article 15 (2017), 15:1–15:15 pages. Google ScholarDigital Library
21. Yong-Jin Liu, Chun-Xu Xu, Dian Fan, and Ying He. 2015. Efficient Construction and Simplification of Delaunay Meshes. ACM Trans. Graph. 34, 6, Article 174 (2015), 174:1–174:13 pages. Google ScholarDigital Library
22. Yong-Jin Liu, Chun-Xu Xu, Ran Yi, Dian Fan, and Ying He. 2016. Manifold Differential Evolution (MDE): A Global Optimization Method for Geodesic Centroidal Voronoi Tessellations on Meshes. ACM Trans. Graph. 35, 6, Article 243 (2016), 243:1–243:10 pages. Google ScholarDigital Library
23. David P. Luebke. 2001. A Developer’s Survey of Polygonal Simplification Algorithms. IEEE Comput. Graph. Appl. 21, 3 (2001), 24–35. Google ScholarDigital Library
24. Manish Mandad, David Cohen-Steiner, and Pierre Alliez. 2015. Isotopic Approximation Within a Tolerance Volume. ACM Trans. Graph. 34, 4, Article 64 (2015), 64:1–64:12 pages. Google ScholarDigital Library
25. Joseph S. B. Mitchell, David M. Mount, and Christos H. Papadimitriou. 1987. The Discrete Geodesic Problem. SIAM J. Comput. 16, 4 (1987), 647–668. Google ScholarDigital Library
26. Igor Rivin. 1994. Euclidean Structures on Simplicial Surfaces and Hyperbolic Volume. Annals of Mathematics 139, 3 (1994), 553–580.Google ScholarCross Ref
27. James C. Spall. 2003. Introduction to Stochastic Search and Optimization. 3rd edition, Wiley. Google ScholarDigital Library
28. Jakob Vesterstrom and Rene Thomsen. 2004. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proc. 6th Congress on Evolutionary Computation. 1980–1987.Google ScholarCross Ref
29. Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv preprint arXiv:1605.04797 (2016).Google Scholar