“A photometric approach for estimating normals and tangents”
Conference:
Type(s):
Title:
- A photometric approach for estimating normals and tangents
Session/Category Title: Image-based capture
Presenter(s)/Author(s):
Abstract:
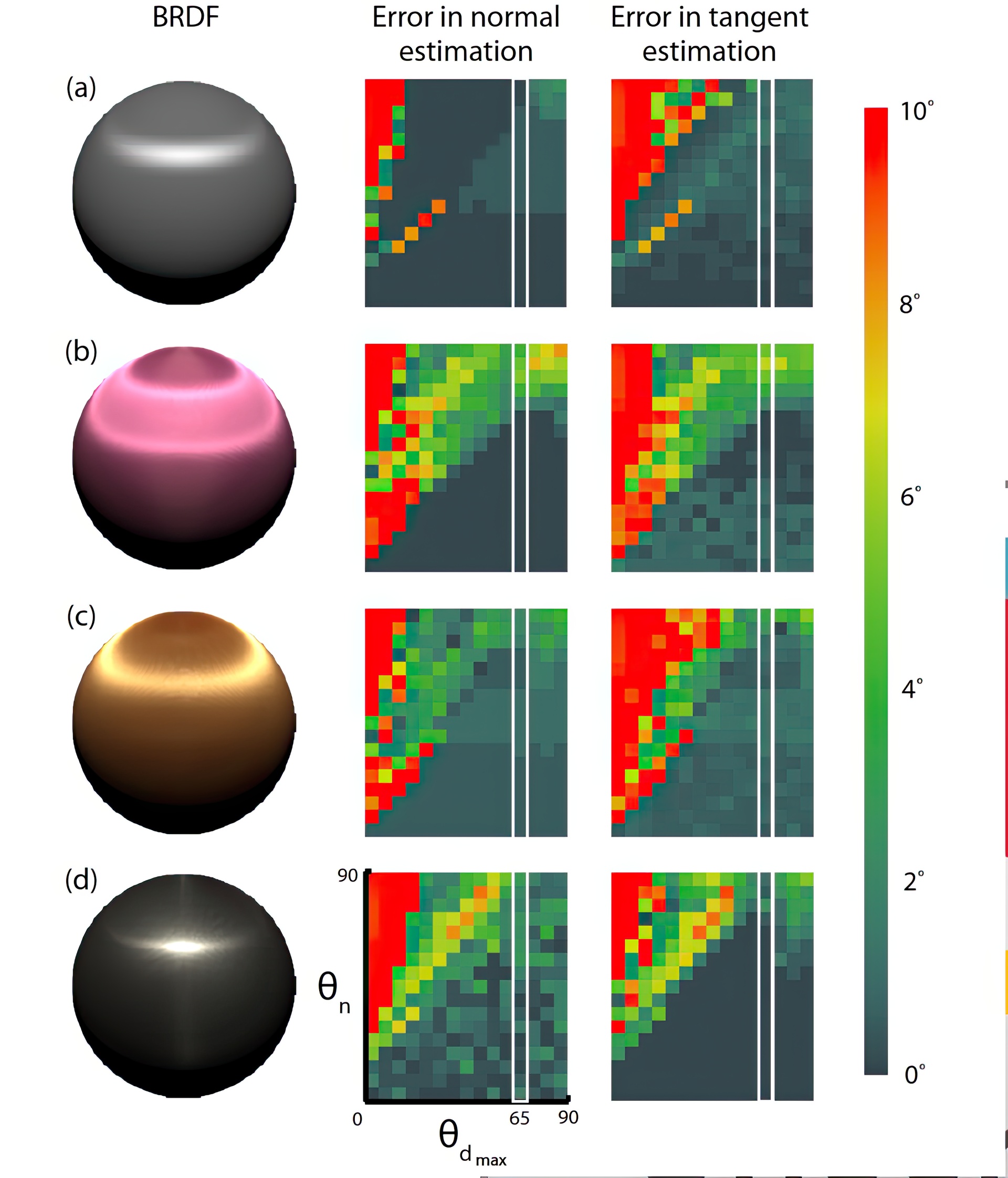
This paper presents a technique for acquiring the shape of real-world objects with complex isotropic and anisotropic reflectance. Our method estimates the local normal and tangent vectors at each pixel in a reference view from a sequence of images taken under varying point lighting. We show that for many real-world materials and a restricted set of light positions, the 2D slice of the BRDF obtained by fixing the local view direction is symmetric under reflections of the halfway vector across the normal-tangent and normal-binormal planes. Based on this analysis, we develop an optimization that estimates the local surface frame by identifying these planes of symmetry in the measured BRDF. As with other photometric methods, a key benefit of our approach is that the input is easy to acquire and is less sensitive to calibration errors than stereo or multi-view techniques. Unlike prior work, our approach allows estimating the surface tangent in the case of anisotropic reflectance. We confirm the accuracy and reliability of our approach with analytic and measured data, present several normal and tangent fields acquired with our technique, and demonstrate applications to appearance editing.
References:
1. Alldrin, N. G., and Kriegman, D. J. 2007. Toward reconstructing surfaces with arbitrary isotropic reflectance: A stratified photometric stereo approach. In Proceedings of the International Conference on Computer Vision (ICCV), 1–8.Google Scholar
2. Alldrin, N., Zickler, T., and Kriegman, D. 2008. Photometric stereo with non-parametric and spatially-varying reflectance. In Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR).Google Scholar
3. Ashikhmin, M., Premoze, S., and Shirley, P. 2000. A microfacet-based BRDF generator. In Proceedings of ACM SIGGRAPH, 65–74. Google Scholar
4. Blinn, J. F. 1977. Models of light reflection for computer synthesized pictures. In Computer Graphics (Proceedings of ACM SIGGRAPH), 192–198. Google Scholar
5. Cabral, B., Olano, M., and Nemec, P. 1999. Reflection space image based rendering. In Proceedings of ACM SIGGRAPH, 165–170. Google Scholar
6. Chen, T. B., Goesele, M., and Seidel, H. P. 2006. Mesostructure from specularity. In Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR), 1825–1832. Google Scholar
7. Chung, H.-S., and Jia, J. 2008. Efficient photometric stereo on glossy surfaces with wide specular lobes. In Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR).Google Scholar
8. Coleman, E., and Jain, R. 1982. Obtaining 3-dimensional shape of textured and specular surfaces using four-source photometry. Computer Vision, Graphics and Image Processing 18, 4, 309–328.Google ScholarCross Ref
9. Cook, R. L., and Torrance, K. E. 1982. A reflectance model for computer graphics. In Computer Graphics (Proceedings of ACM SIGGRAPH), 7–24. Google Scholar
10. Fisher, M., Schroder, P., Desbrun, M., and Hoppe, H. 2007. Design of tangent vector fields. ACM Transactions on Graphics (TOG) 26, 3. Google ScholarDigital Library
11. Francken, Y., Cuypers, T., Mertens, T., Gielis, J., and Bekaert, P. 2008. High quality mesostructure acquisition using specularities. In Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR).Google Scholar
12. Georghiades, A. S. 2003. Incorporating the Torrance and Sparrow model of reflectance in uncalibrated photometric stereo. In Proceedings of the International Conference on Computer Vision (ICCV), 816–823. Google Scholar
13. Goldman, D. B., Curless, B., Hertzmann, A., and Seitz, S. M. 2005. Shape and spatially-varying BRDFs from photometric stereo. In Proceedings of the International Conference on Computer Vision, 341–348. Google Scholar
14. He, X. D., Torrance, K. E., Sillion, F., and Greenberg, D. P. 1991. A comprehensive physical model for light reflection. In Computer Graphics (Proceedings of ACM SIGGRAPH). Google Scholar
15. Heidrich, W., and Seidel, H.-P. 1999. Realistic, hardware-accelerated shading and lighting. In Proceedings of ACM SIGGRAPH), 171–178. Google Scholar
16. Hertzmann, A., and Seitz, S. 2003. Shape and materials by example: a photometric stereo approach. IEEE Computer Vision and Pattern Recognition, 2003. 1, 533–540. Google ScholarDigital Library
17. Lawrence, J., Ben-Artzi, A., DeCoro, C., Matusik, W., Pfister, H., Ramamoorthi, R., and Rusinkiewicz, S. 2006. Inverse shade trees for non-parametric material representation and editing. ACM Transactions on Graphics (TOG) 25, 3, 735–745. Google ScholarDigital Library
18. Ma, W.-C., Hawkins, T., Peers, P., Chabert, C.-F., Weiss, M., and Debevec, P. 2007. Rapid acquisition of specular and diffuse normal maps from polarized spherical gradient illumination. In Proceedings of Eurographics Symposium on Rendering. Google Scholar
19. Mallick, S., Zickler, T., Kriegman, D., and Belhumeur, P. 2005. Beyond Lambert: Reconstructing specular surfaces using color. Proc. IEEE Conf. Computer Vision and Pattern Recognition 2, 619–626. Google Scholar
20. Masselus, V., Dutré, P., and Anrys, F. 2002. The free-form light stage. In Proceedings of the Eurographics Workshop on Rendering. Google ScholarDigital Library
21. Nayar, S., Ikeuchi, K., and Kanade, T. 1990. Determining shape and reflectance of hybrid surfaces by photometricsampling. Robotics and Automation, IEEE Transactions on 6, 4, 418–431.Google Scholar
22. Nayar, S. K., Krishnan, G., Grossberg, M. D., and Raskar, R. 2006. Fast separation of direct and global components of a scene using high frequency illumination. ACM Transactions on Graphics 25, 3. Google ScholarDigital Library
23. Nelder, J., and Mead, R. 1965. A simplex method for function minimization. Computer Journal 7, 308–311.Google ScholarCross Ref
24. Ngan, A., Durand, F., and Matusik, W. 2005. Experimental analysis of BRDF models. In Proceedings of the Eurographics Symposium on Rendering, 117–126. Google Scholar
25. Nicodemus, F. E., Richmond, J. C., and Hsia, J. J. 1977. Geometrical considerations and reflectance. National Bureau of Standards.Google Scholar
26. Podolak, J., Shilane, P., Golovinskiy, A., Rusinkiewicz, S., and Funkhouser, T. 2006. A planar-reflective symmetry transform for 3D shapes. ACM Transactions on Graphics 25, 3. Google ScholarDigital Library
27. Rusinkiewicz, S. 1998. A new change of variables for efficient BRDF representation. In Proceedings of the Eurugraphics Rendering Workshop, 11–22.Google Scholar
28. Schlick, C. 1994. An inexpensive BRDF model for physically-based rendering. Computer Graphics Forum 13, 3, 233–246.Google ScholarCross Ref
29. Shewchuk, J. R. 1996. Triangle: Engineering a 2D quality mesh generator and delaunay triangulator. In Applied Computational Geometry: Towards Geometric Engineering, M. C. Lin and D. Manocha, Eds., vol. 1148 of Lecture Notes in Computer Science. Springer-Verlag, may, 203–222. Google ScholarDigital Library
30. Stanford, 2002. Stanford graphics lab spherical gantry (http://graphics.stanford.edu/projects/gantry/).Google Scholar
31. Stark, M., Arvo, J., and Smits, B. 2005. Barycentric parameterizations for isotropic BRDFs. IEEE Transactions on Visualization and Computer Graphics, 126–138. Google Scholar
32. Tagare, H. D., and deFigueiredo, R. J. P. 1991. A theory of photometric stereo for a class of diffuse non-lambertian surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence 13, 2. Google ScholarDigital Library
33. Toler-Franklin, C., Finkelstein, A., and Rusinkiewicz, S. 2007. Illustration of complex real-world objects using images with normals. In International Symposium on Non-Photorealistic Animation and Rendering. Google Scholar
34. Torrance, K. E., and Sparrow, M. E. 1967. Theory for off-specular reflection from roughened surfaces. Journal of the Optical Society of America 57, 1105–1114.Google ScholarCross Ref
35. Wang, J., and Dana, K. J. 2006. Relief textures from specularities. IEEE Transactions on Pattern Analysis and Machine Intelligence 28, 3, 446–457. Google ScholarDigital Library
36. Ward, G. J. 1992. Measuring and modeling anisotropic reflection. In Computer Graphics (Proceedings of ACM SIGGRAPH), 265–272. Google Scholar
37. Woodham, R. J. 1980. Photometric method for determining surface orientation from multiple images. Optical Engineering 19, 1, 139–144.Google ScholarCross Ref
38. Zickler, T., Belhumeur, P. N., and Kriegman, D. J. 2002. Helmholtz stereopsis: Exploiting reciprocity for surface reconstruction. International Journal of Computer Vision 49, 2–3, 215–227. Google ScholarCross Ref