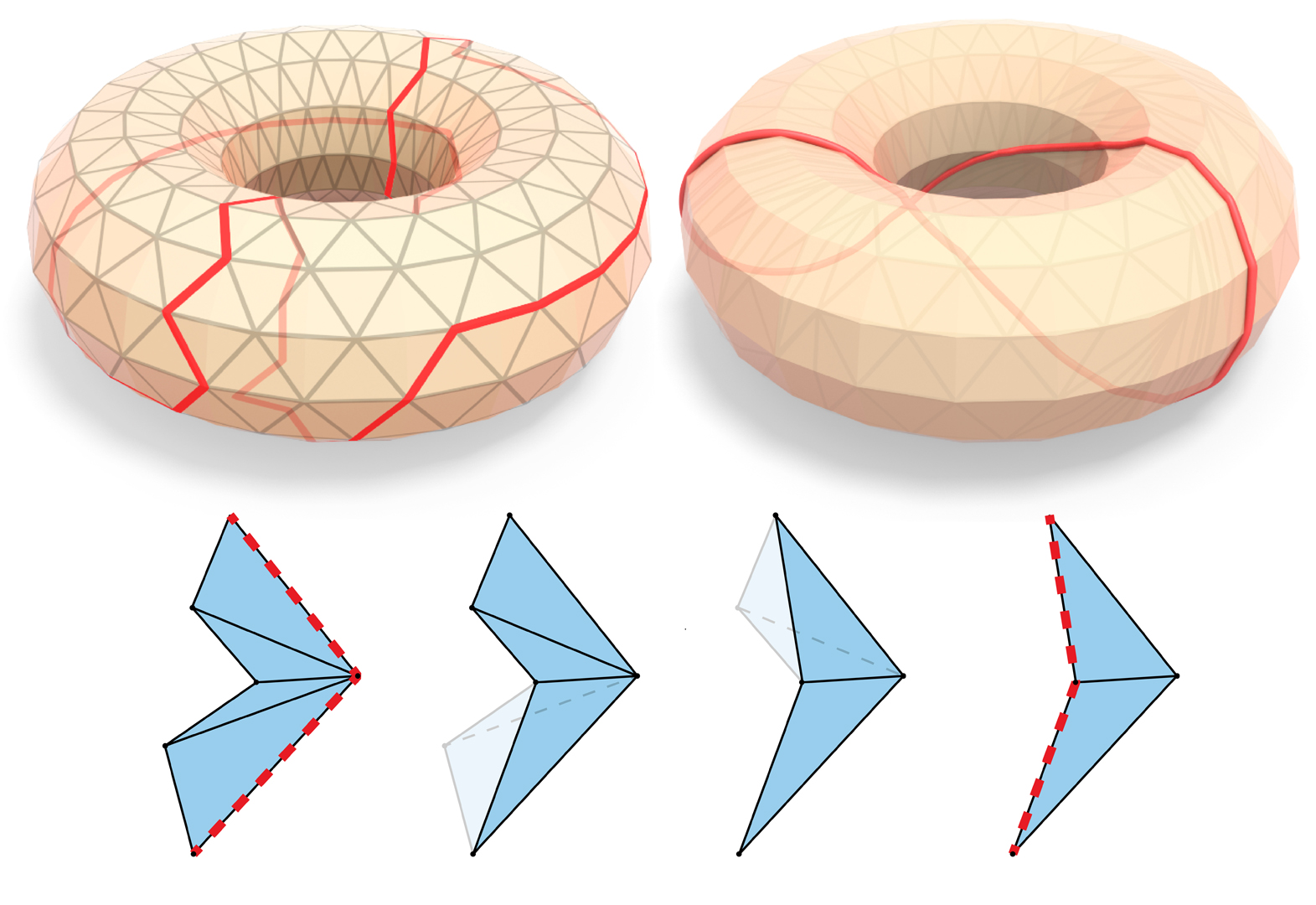
“You can find geodesic paths in triangle meshes by just flipping edges” by Sharp and Crane
Conference:
Type(s):
Title:
- You can find geodesic paths in triangle meshes by just flipping edges
Session/Category Title:
- Meticulous Meshes
Presenter(s)/Author(s):
Abstract:
This paper introduces a new approach to computing geodesics on polyhedral surfaces—the basic idea is to iteratively perform edge flips, in the same spirit as the classic Delaunay flip algorithm. This process also produces a triangulation conforming to the output geodesics, which is immediately useful for tasks in geometry processing and numerical simulation. More precisely, our FlipOut algorithm transforms a given sequence of edges into a locally shortest geodesic while avoiding self-crossings (formally: it finds a geodesic in the same isotopy class). The algorithm is guaranteed to terminate in a finite number of operations; practical runtimes are on the order of a few milliseconds, even for meshes with millions of triangles. The same approach is easily applied to curves beyond simple paths, including closed loops, curve networks, and multiply-covered curves. We explore how the method facilitates tasks such as straightening cuts and segmentation boundaries, computing geodesic Bézier curves, extending the notion of constrained Delaunay triangulations (CDT) to curved surfaces, and providing accurate boundary conditions for partial differential equations (PDEs). Evaluation on challenging datasets such as Thingi10k indicates that the method is both robust and efficient, even for low-quality triangulations.
References:
1. Y. Adikusuma, Z. Fang, and Y. He. 2020. Fast Construction of Discrete Geodesic Graphs. ACM Trans. Graph. 39, 2 (2020).Google ScholarDigital Library
2. P. An. 2019. Finding Shortest Paths in a Sequence of Triangles in 3D by the Planar Unfolding. Numerical Functional Analysis and Optimization 40, 8 (2019), 944–952.Google ScholarCross Ref
3. E. Appleboim, E. Saucan, and J. Stern. 2009. Normal Approximations of Geodesics on Smooth Triangulated Surfaces. Technical Report. CCIT Report.Google Scholar
4. J. Athreya, D. Aulicino, and W. Hooper. 2020. Platonic Solids and High Genus Covers of Lattice Surfaces. Experimental Mathematics (2020).Google Scholar
5. M. Bell. 2016. Simplifying Triangulations. arXiv:1604.04314 (2016).Google Scholar
6. M. Bern, D. Eppstein, and J. Erickson. 2002. Flipping Cubical Meshes. Engineering with Computers 18, 3 (2002), 173–187.Google ScholarCross Ref
7. A. Bobenko and B. Springborn. 2007. A Discrete Laplace-Beltrami Operator for Simplicial Surfaces. Discrete & Computational Geometry 38, 4 (2007).Google Scholar
8. D. Bommes and L. Kobbelt. 2007. Accurate Computation of Geodesic Distance Fields for Polygonal Curves on Triangle Meshes. In VMV, Vol. 7. 151–160.Google Scholar
9. P. Bose, A. Maheshwari, C. Shu, and S. Wuhrer. 2011. A Survey of Geodesic Paths on 3D Surfaces. Comput. Geom. Theory Appl. 44, 9 (Nov. 2011), 13.Google Scholar
10. S. Callens and A. Zadpoor. 2018. From Flat Sheets to Curved Geometries: Origami and Kirigami Approaches. Materials Today 21, 3 (2018), 241 — 264.Google ScholarCross Ref
11. M. Campen, M. Heistermann, and L. Kobbelt. 2013. Practical Anisotropic Geodesy. In Computer Graphics Forum, Vol. 32. Wiley Online Library, 63–71.Google Scholar
12. L. Cao, J. Zhao, J. Xu, S. Chen, G. Liu, S. Xin, Y. Zhou, and Y. He. 2020. Computing Smooth Quasi-geodesic Distance Field (QGDF) with Quadratic Programming. Computer-Aided Design (2020).Google Scholar
13. X. Chen, A. Golovinskiy, and T. Funkhouser. 2009. A Benchmark for 3D Mesh Segmentation. ACM Trans. Graph. (Proc. SIGGRAPH) 28, 3 (Aug. 2009).Google ScholarDigital Library
14. L. Chew. 1989. Constrained Delaunay Triangulations. Algorithmica 4, 1–4 (1989).Google Scholar
15. L. Chew. 1993. Guaranteed-quality Mesh Generation for Curved Surfaces. In Proceedings of the Ninth Annual Symposium on Computational Geometry (SCG ’93).Google ScholarDigital Library
16. K. Crane, M. Livesu, E. Puppo, and Y. Qin. 2020. A Survey of Algorithms for Geodesic Paths and Distances. arXiv:2007.10430 (2020).Google Scholar
17. K. Crane and M. Wardetzky. 2017. A Glimpse Into Discrete Differential Geometry. Notices of the American Mathematical Society 64, 10 (November 2017), 1153–1159.Google ScholarCross Ref
18. K. Crane, C. Weischedel, and M. Wardetzky. 2013. Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow. ACM Trans. Graph. 32, 5 (Oct. 2013).Google ScholarDigital Library
19. M. Crofton. 1868. On the Theory of Local Probability, Applied to Straight Lines Drawn at Random in a Plane; the Methods Used Being Also Extended to the Proof of Certain New Theorems in the Integral Calculus. Philosophical Transactions of the Royal Society of London 158 (1868), 181–199.Google ScholarCross Ref
20. R. Dyer, H. Zhang, and T. Möller. 2007. Delaunay Mesh Construction. Proceedings of the 5th Eurographics Symposium on Geometry Processing.Google Scholar
21. J. Erickson. 2014. Efficiently Hex-meshing Things with Topology. Discrete & Computational Geometry 52, 3 (2014), 427–449.Google ScholarDigital Library
22. M. Fisher, B. Springborn, P. Schröder, and A. Bobenko. 2007. An Algorithm for the Construction of Intrinsic Delaunay Triangulations with Applications to Digital Geometry Processing. Computing 81, 2 (Nov 2007).Google ScholarDigital Library
23. M. Gage. 1990. Curve Shortening on Surfaces. Annales scientifiques de l’École Normale Supérieure Ser. 4, 23, 2 (1990), 229–256.Google Scholar
24. X. Han, H. Yu, Y. Yu, and J. Zhang. 2017. A Fast Propagation Scheme for Approximate Geodesic Paths. Graphical Models 91 (2017), 22 — 29.Google ScholarCross Ref
25. J. Hass and P. Scott. 1994. Shortening Curves on Surfaces. Topology 33, 1 (1994).Google Scholar
26. A. Hatcher. 2002. Algebraic Topology. Cambridge University Press.Google Scholar
27. P. Herholz and M. Alexa. 2019. Efficient Computation of Smoothed Exponential Maps. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 79–90.Google Scholar
28. C. Indermitte, T. Liebling, M. Troyanov, and H. Clémençon. 2001. Voronoi Diagrams on Piecewise Flat Surfaces and an Application to Biological Growth. Theoretical Computer Science 263 (2001).Google Scholar
29. S. Kapoor. 1999. Efficient Computation of Geodesic Shortest Paths. In Proceedings of the thirty-first annual ACM symposium on Theory of computing.Google ScholarDigital Library
30. L. Kharevych, B. Springborn, and P. Schröder. 2006. Discrete Conformal Mappings via Circle Patterns. ACM Trans. Graph. 25, 2 (2006).Google ScholarDigital Library
31. S. Kiazyk, S. Loriot, and E. Colin de Verdière. 2015. CGAL 5.0.2—Triangulated Surface Mesh Shortest Paths. http://www.cgal.org.Google Scholar
32. R. Kimmel and J. Sethian. 1998. Fast Marching Methods on Triangulated Domains. Proc. Nat. Acad. Sci. 95 (1998).Google Scholar
33. D. Kirsanov. 2008. Implementation of Exact Geodesics on Triangular Meshes. code.google.com/archive/p/geodesic/.Google Scholar
34. F. Knöppel, K. Crane, U. Pinkall, and P. Schröder. 2013. Globally Optimal Direction Fields. ACM Trans. Graph. 32, 4 (2013).Google ScholarDigital Library
35. C. Lawson. 1977. Software for C1 Surface Interpolation. In Mathematical software. Elsevier, 161–194.Google Scholar
36. B. Liu, S. Chen, S. Xin, Y. He, Z. Liu, and J. Zhao. 2017a. An Optimization-driven Approach for Computing Geodesic Paths on Triangle Meshes. Computer-Aided Design 90 (2017).Google Scholar
37. Y. Liu, D. Fan, C. Xu, and Y. He. 2017b. Constructing Intrinsic Delaunay Triangulations from the Dual of Geodesic Voronoi Diagrams. ACM Trans. Graph. 36, 2 (2017).Google ScholarDigital Library
38. Y. Liu, C. Xu, D. Fan, and Y. He. 2015. Efficient Construction and Simplification of Delaunay Meshes. ACM Trans. Graph. 34, 6 (2015).Google ScholarDigital Library
39. V. Lucquin, S. Deguy, and T. Boubekeur. 2017. SeamCut: Interactive Mesh Segmentation for Parameterization. In ACM SIGGRAPH 2017 Technical Briefs.Google Scholar
40. D. Martínez, L. Velho, and P. Carvalho. 2005. Computing Geodesics on Triangular Meshes. Computers & Graphics 29, 5 (2005).Google Scholar
41. J. Mitchell, D. Mount, and C. Papadimitriou. 1987. The Discrete Geodesic Problem. SIAM J. Comput. 16, 4 (Aug. 1987), 22.Google ScholarDigital Library
42. D. Morera, P. Carvalho, and L. Velho. 2008. Modeling on Triangulations with Geodesic Curves. The Visual Computer 24, 12 (Dec 2008).Google ScholarDigital Library
43. A. Myles, N. Pietroni, and D. Zorin. 2014. Robust Field-aligned Global Parametrization. ACM Trans. Graph. 33, 4 (2014).Google ScholarDigital Library
44. G. Patané. 2016. STAR—Laplacian Spectral Kernels and Distances for Geometry Processing and Shape Analysis. In Computer Graphics Forum.Google Scholar
45. G. Peyré and L. Cohen. 2005. Heuristically Driven Front Propagation for Geodesic Paths Extraction. In International Workshop on Variational, Geometric, and Level Set Methods in Computer Vision. Springer, 173–185.Google Scholar
46. K. Polthier and M. Schmies. 2006. Straightest Geodesics on Polyhedral Surfaces. In ACM SIGGRAPH 2006 Courses.Google Scholar
47. Y. Qin, X. Han, H. Yu, Y. Yu, and J. Zhang. 2016. Fast and Exact Discrete Geodesic Computation based on Triangle-oriented Wavefront Propagation. ACM Trans. Graph. 35, 4 (2016).Google ScholarDigital Library
48. M. Remešíková, M. Šagát, and P. Novysedlák. 2019. Discrete Lagrangian Algorithm for Finding Geodesics on Triangular Meshes. Applied Mathematical Modelling (2019).Google Scholar
49. I. Rivin. 1994. Euclidean Structures on Simplicial Surfaces and Hyperbolic Volume. Annals of mathematics 139, 3 (1994).Google ScholarCross Ref
50. R. Schmidt, C. Grimm, and B. Wyvill. 2006. Interactive Decal Compositing with Discrete Exponential Maps. In ACM SIGGRAPH 2006 Papers.Google Scholar
51. J. Sethian. 1989. A Review of Recent Numerical Algorithms for Hypersurfaces Moving with Curvature Dependent Speed. J. Differential Geometry 31 (1989), 131–161.Google ScholarCross Ref
52. N. Sharp and K. Crane. 2018. Variational Surface Cutting. ACM Trans. Graph. 37, 4 (2018).Google ScholarDigital Library
53. N. Sharp and K. Crane. 2020. A Laplacian for Nonmanifold Triangle Meshes. Computer Graphics Forum (SGP) 39, 5 (2020).Google Scholar
54. N. Sharp, K. Crane, et al. 2019a. geometry-central. www.geometry-central.net.Google Scholar
55. N. Sharp, Y. Soliman, and K. Crane. 2019b. Navigating Intrinsic Triangulations. ACM Trans. Graph. 38, 4 (2019).Google ScholarDigital Library
56. N. Sharp, Y. Soliman, and K. Crane. 2019c. The Vector Heat Method. ACM Trans. Graph. 38, 3 (2019).Google ScholarDigital Library
57. J. Shewchuk. 1997. Delaunay Refinement Mesh Generation. Ph.D. Dissertation. Carnegie Mellon University. Tech Report CMU-CS-97-137.Google Scholar
58. P. Shilane, P. Min, M. Kazhdan, and T. Funkhouser. 2004. The Princeton Shape Benchmark. In Proceedings Shape Modeling Applications, 2004. IEEE.Google Scholar
59. B. Springborn. 2019. Ideal Hyperbolic Polyhedra and Discrete Uniformization. Discrete & Computational Geometry (Sep 2019).Google Scholar
60. B. Springborn, P. Schröder, and U. Pinkall. 2008. Conformal Equivalence of Triangle Meshes. ACM Trans. Graph. 27, 3 (2008).Google ScholarDigital Library
61. V. Surazhsky, T. Surazhsky, D. Kirsanov, S. Gortler, and H. Hoppe. 2005. Fast Exact and Approximate Geodesics on Meshes. ACM Trans. Graph. 24, 3 (2005).Google ScholarDigital Library
62. X. Wang, Z. Fang, J. Wu, S. Xin, and Y. He. 2017. Discrete Geodesic Graph for Computing Geodesic Distances on Polyhedral Surfaces. Computer Aided Geometric Design 52 (2017).Google Scholar
63. J. Weeks. 1993. Convex Hulls and Isometries of Cusped Hyperbolic 3-manifolds. Topology and its Applications 52, 2 (1993).Google Scholar
64. C. Wu and X. Tai. 2010. A Level Set Formulation of Geodesic Curvature Flow on Simplicial Surfaces. IEEE Transactions on Visualization and Computer Graphics 16, 4 (July 2010).Google Scholar
65. S. Xin, Y. He, and C. Fu. 2011. Efficiently Computing Exact Geodesic Loops within Finite Steps. IEEE Transactions on Visualization and Computer Graphics 18, 6 (2011).Google Scholar
66. S. Xin and G. Wang. 2007. Efficiently Determining a Locally Exact Shortest Path on Polyhedral Surfaces. Computer-Aided Design 39, 12 (2007).Google Scholar
67. S. Xin and G. Wang. 2009. Improving Chen and Han’s Algorithm on the Discrete Geodesic Problem. ACM Trans. Graph. 28, 4 (2009).Google ScholarDigital Library
68. C. Xu, T. Wang, Y. Liu, L. Liu, and Y. He. 2015. Fast Wavefront Propagation for Computing Exact Geodesic Distances on Meshes. IEEE transactions on visualization and computer graphics 21, 7 (2015).Google Scholar
69. X. Ying, C. Huang, X. Fu, Y. He, R. Yu, J. Wang, and M. Yu. 2019. Parallelizing Discrete Geodesic Algorithms with Perfect Efficiency. Computer-Aided Design 115 (2019).Google Scholar
70. X. Ying, X. Wang, and Y. He. 2013. Saddle Vertex Graph: a Novel Solution to the Discrete Geodesic Problem. ACM Trans. Graph. 32, 6 (2013).Google ScholarDigital Library
71. X. Ying, S. Xin, and Y. He. 2014. Parallel Chen-Han (PCH) Algorithm for Discrete Geodesics. ACM Trans. Graph. 33, 1 (2014).Google ScholarDigital Library
72. J. Zhang, C. Wu, J. Cai, J. Zheng, and X. Tai. 2010. Mesh snapping: Robust Interactive Mesh Cutting Using Fast Geodesic Curvature Flow. In Computer graphics forum, Vol. 29. Wiley Online Library.Google Scholar
73. Q. Zhou and A. Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv:1605.04797 (2016).Google Scholar