“To cut or to fill: a global optimization approach to topological simplification” by Zeng, Chambers, Letscher and Ju – ACM SIGGRAPH HISTORY ARCHIVES

“To cut or to fill: a global optimization approach to topological simplification” by Zeng, Chambers, Letscher and Ju

  • 2020 SA Technical Papers_Zeng_To cut or to fill: a global optimization approach to topological simplification

Conference:


Type(s):


Title:

    To cut or to fill: a global optimization approach to topological simplification

Session/Category Title:   Digital Geometry Processing

Presenter(s)/Author(s):


Abstract:


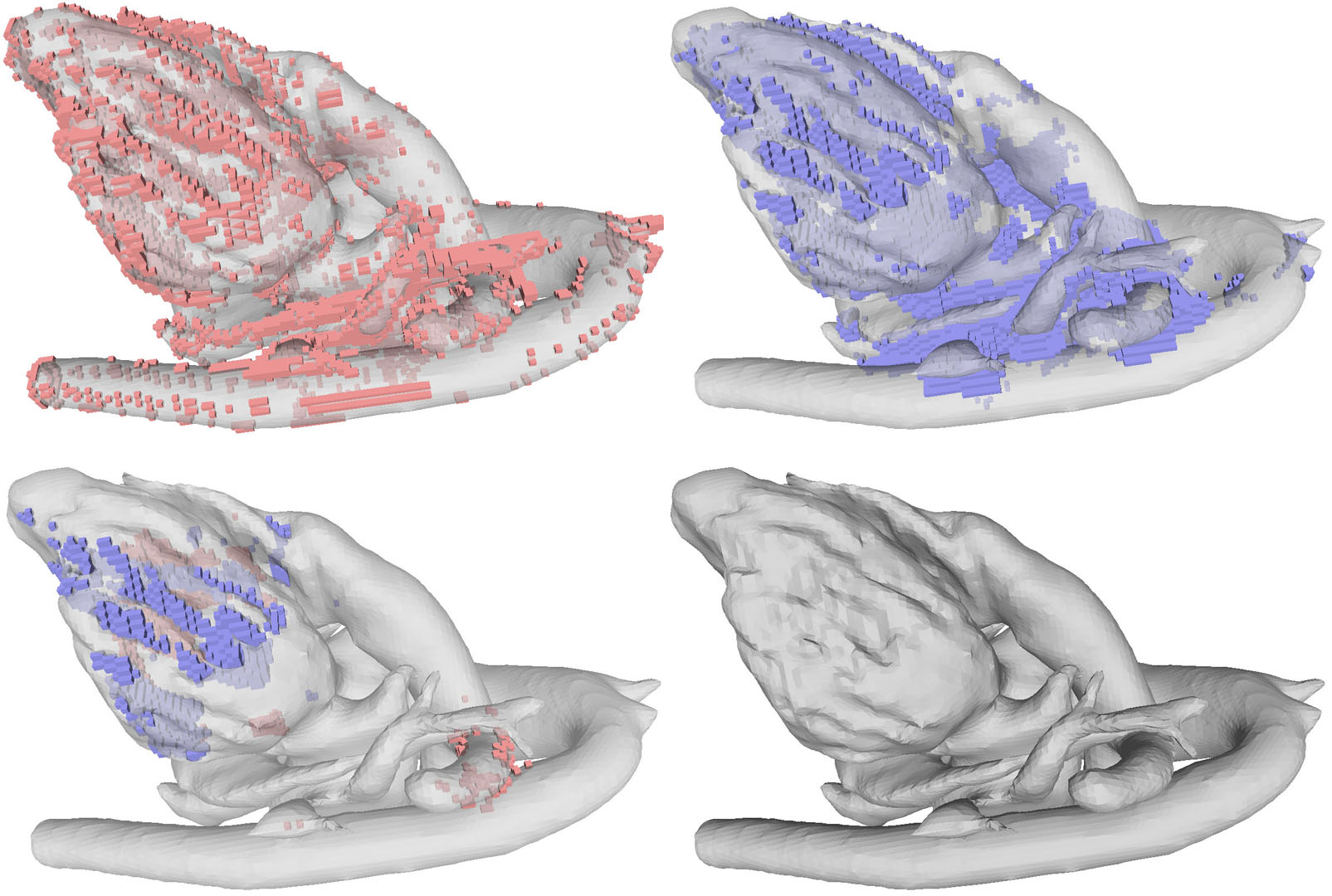
    We present a novel algorithm for simplifying the topology of a 3D shape, which is characterized by the number of connected components, handles, and cavities. Existing methods either limit their modifications to be only cutting or only filling, or take a heuristic approach to decide where to cut or fill. We consider the problem of finding a globally optimal set of cuts and fills that achieve the simplest topology while minimizing geometric changes. We show that the problem can be formulated as graph labelling, and we solve it by a transformation to the Node-Weighted Steiner Tree problem. When tested on examples with varying levels of topological complexity, the algorithm shows notable improvement over existing simplification methods in both topological simplicity and geometric distortions.

References:


    1. 2014. 11th DIMACS Implementation Challenge in Collaboration with ICERM: Steiner Tree Problems. http://dimacs11.zib.de/Google Scholar
    2. Dominique Attali, Ulrich Bauer, Olivier Devillers, Marc Glisse, and André Lieutier. 2015. Homological reconstruction and simplification in R3. Computational Geometry 48, 8 (2015), 606–621.Google ScholarDigital Library
    3. Marco Attene, Marcel Campen, and Leif Kobbelt. 2013. Polygon Mesh Repairing: An Application Perspective. ACM Comput. Surv. 45, 2 (March 2013), 15:1–15:33.Google ScholarDigital Library
    4. Ulrich Bauer, Michael Kerber, and Jan Reininghaus. 2014. Distributed computation of persistent homology. In 2014 proceedings of the sixteenth workshop on algorithm engineering and experiments (ALENEX). SIAM, 31–38.Google ScholarCross Ref
    5. Stephan Bischoff and Leif Kobbelt. 2002. Isosurface Reconstruction with Topology Control.. In Pacific Conference on Computer Graphics and Applications. 246–255.Google ScholarCross Ref
    6. Yuri Boykov, Olga Veksler, and Ramin Zabih. 2001. Fast approximate energy minimization via graph cuts. IEEE Transactions on pattern analysis and machine intelligence 23, 11 (2001), 1222–1239.Google ScholarDigital Library
    7. Erin W Chambers, Tao Ju, David Letscher, Mao Li, and Christopher Topp. 2018. Some Heuristics for the Homological Simplification Problem. In CCCG.Google Scholar
    8. Lin Chen and Gudrun Wagenknecht. 2006. Automated topology correction for human brain segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 316–323.Google ScholarDigital Library
    9. Xiao Han, Chenyang Xu, Ulisses Braga-Neto, and Jerry L. Prince. 2002. Topology Correction in Brain Cortex Segmentation Using a Multi-Scale, Graph-Based Algorithm. IEEE Trans. Med. Imaging 21, 2 (2002), 109–121.Google ScholarCross Ref
    10. Xiao Han, Chenyang Xu, and Jerry L. Prince. 2003. A topology preserving level set method for geometric deformable models. IEEE Transactions on Pattern Analysis and Machine Intelligence 25, 6 (2003), 755–768.Google ScholarDigital Library
    11. Allen Hatcher. 2002. Algebraic Topology. Cambridge University Pres.Google Scholar
    12. Zhiyang Huang, Ming Zou, Nathan Carr, and Tao Ju. 2017. Topology-controlled Reconstruction of Multi-labelled Domains from Cross-sections. ACM Transactions on Graphics (TOG) 36, 4 (2017), 1–12.Google ScholarDigital Library
    13. Tao Ju, Qian-Yi Zhou, and Shi-Min Hu. 2007. Editing the Topology of 3D Models by Sketching. ACM Trans. Graph. 26, 3, Article 42 (July 2007). Google ScholarDigital Library
    14. N. Kriegeskorte and R. Goebel. 2001. An efficient algorithm for topologically correct segmentation of the cortical sheet in anatomical mr volumes. Neuroimage 14, 2 (August 2001), 329–346.Google ScholarCross Ref
    15. Roee Lazar, Nadav Dym, Yam Kushinsky, Zhiyang Huang, Tao Ju, and Yaron Lipman. 2018. Robust optimization for topological surface reconstruction. ACM Transactions on Graphics (TOG) 37, 4 (2018), 1–10.Google ScholarDigital Library
    16. Markus Leitner, Ivana Ljubić, Martin Luipersbeck, and Markus Sinnl. 2018. A dual ascent-based branch-and-bound framework for the prize-collecting steiner tree and related problems. INFORMS Journal on Computing 30, 2 (2018), 402–420.Google ScholarDigital Library
    17. Fakir S. Nooruddin and Greg Turk. 2003. Simplification and Repair of Polygonal Models Using Volumetric Techniques. IEEE Trans. Vis. Comput. Graph. 9, 2 (2003), 191–205.Google ScholarDigital Library
    18. Florent Ségonne. 2008. Active contours under topology control – genus preserving level sets. International Journal of Computer Vision 79, 2 (2008), 107–117.Google ScholarDigital Library
    19. Florent Ségonne, Jenni Pacheco, and Bruce Fischl. 2007. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE transactions on medical imaging 26, 4 (2007), 518–529.Google ScholarCross Ref
    20. Andrei Sharf, Thomas Lewiner, Ariel Shamir, Leif Kobbelt, and Daniel Cohen-Or. 2006. Competing fronts for coarse-to-fine surface reconstruction. In Eurographics. Vienna, 389–398. http://www.mat.puc-rio.br/~tomlew/competing_fronts_eg.pdfGoogle Scholar
    21. Andrei Sharf, Thomas Lewiner, Gil Shklarski, Sivan Toledo, and Daniel Cohen-Or. 2007. Interactive Topology-aware Surface Reconstruction. ACM Trans. Graph. 26, 3 (July 2007).Google ScholarDigital Library
    22. David W. Shattuck and Richard M. Leahy. 2001. Automated Graph Based Analysis and Correction of Cortical Volume Topology. IEEE Trans. Med. Imaging 20, 11 (2001), 1167–1177.Google ScholarCross Ref
    23. Andrzej Szymczak and James Vanderhyde. 2003. Extraction of topologically simple isosurfaces from volume datasets. In IEEE Visualization. 67–74.Google Scholar
    24. Zoë J. Wood, Hugues Hoppe, Mathieu Desbrun, and Peter Schröder. 2004. Removing excess topology from isosurfaces. ACM Trans. Graph. 23, 2 (2004), 190–208.Google ScholarDigital Library
    25. Kangxue Yin, Hui Huang, Hao Zhang, Minglun Gong, Daniel Cohen-Or, and Baoquan Chen. 2014. Morfit: Interactive Surface Reconstruction from Incomplete Point Clouds with Curve-driven Topology and Geometry Control. ACM Trans. Graph. 33, 6 (Nov. 2014), 202:1–202:12.Google ScholarDigital Library
    26. Yun Zeng, Dimitris Samaras, Wei Chen, and Qunsheng Peng. 2008. Topology cuts: A novel min-cut/max-flow algorithm for topology preserving segmentation in N-D images. Computer Vision and Image Understanding 112, 1 (2008), 81–90.Google ScholarDigital Library
    27. Qian-Yi Zhou, Tao Ju, and Shi-Min Hu. 2007. Topology Repair of Solid Models Using Skeletons. IEEE Transactions on Visualization and Computer Graphics 13, 4 (July 2007), 675–685.Google ScholarDigital Library
    28. Ming Zou, Michelle Holloway, Nathan Carr, and Tao Ju. 2015. Topology-constrained surface reconstruction from cross-sections. ACM Trans. Graph. 34, 4 (2015), 128.Google ScholarDigital Library

ACM Digital Library Publication:


Overview Page:


Submit a story:

If you would like to submit a story about this presentation, please contact us: historyarchives@siggraph.org