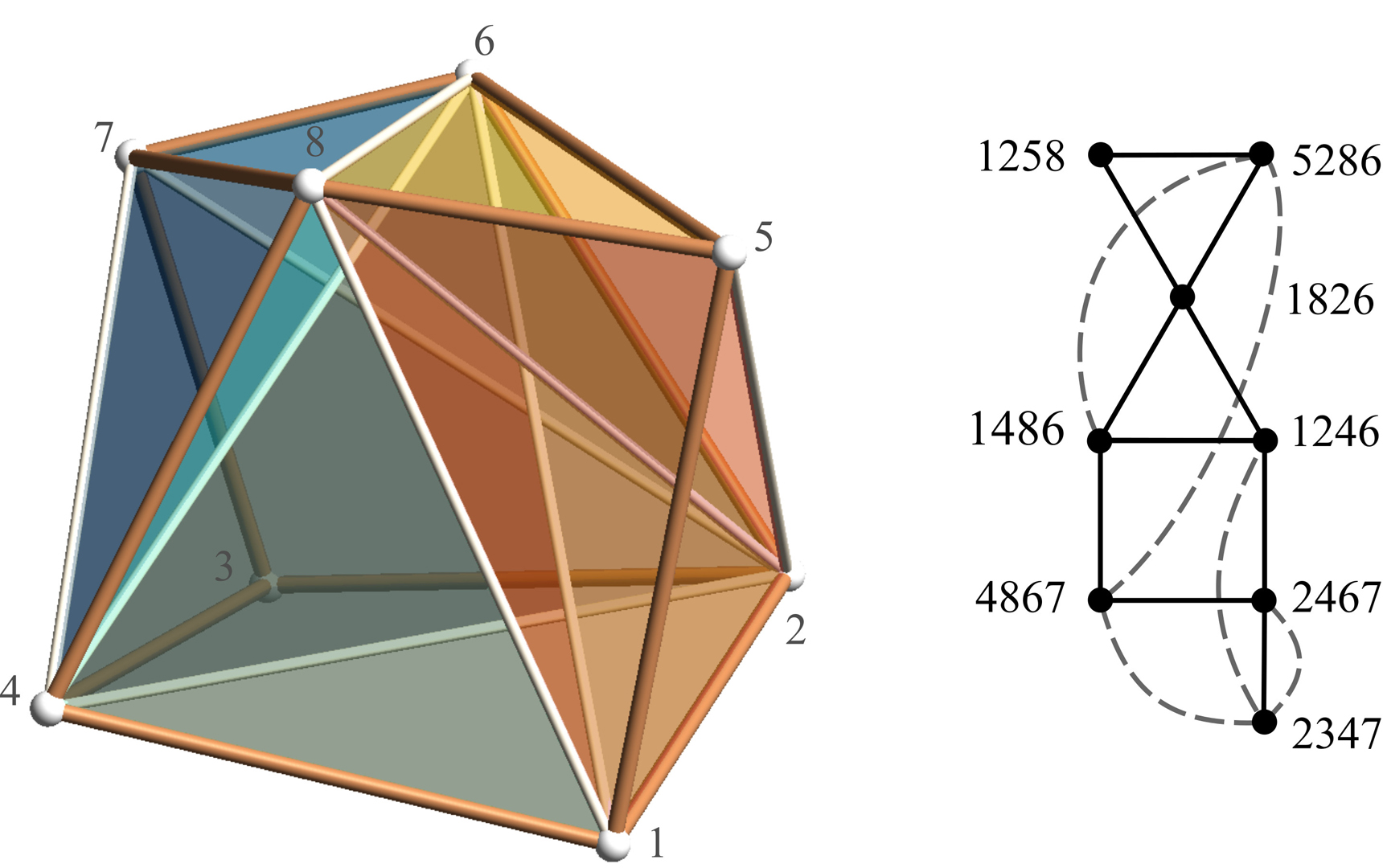
“There are 174 subdivisions of the hexahedron into tetrahedra”
Conference:
Type(s):
Title:
- There are 174 subdivisions of the hexahedron into tetrahedra
Session/Category Title:
- Meshing
Presenter(s)/Author(s):
Moderator(s):
Abstract:
This article answers an important theoretical question: How many different subdivisions of the hexahedron into tetrahedra are there? It is well known that the cube has five subdivisions into 6 tetrahedra and one subdivision into 5 tetrahedra. However, all hexahedra are not cubes and moving the vertex positions increases the number of subdivisions. Recent hexahedral dominant meshing methods try to take these configurations into account for combining tetrahedra into hexahedra, but fail to enumerate them all: they use only a set of 10 subdivisions among the 174 we found in this article.The enumeration of these 174 subdivisions of the hexahedron into tetrahedra is our combinatorial result. Each of the 174 subdivisions has between 5 and 15 tetrahedra and is actually a class of 2 to 48 equivalent instances which are identical up to vertex relabeling. We further show that exactly 171 of these subdivisions have a geometrical realization, i.e. there exist coordinates of the eight hexahedron vertices in a three-dimensional space such that the geometrical tetrahedral mesh is valid. We exhibit the tetrahedral meshes for these configurations and show in particular subdivisions of hexahedra with 15 tetrahedra that have a strictly positive Jacobian.
References:
1. Amos Altshuler, J. Bokowski, and Leon Steinberg. 1980. The classification of simplicial 3-spheres with nine vertices into polytopes and nonpolytopes. Discrete Mathematics 31, 2 (1980), 115–124. Google ScholarDigital Library
2. Amos Altshuler and Leon Steinberg. 1973. Neighborly 4-polytopes with 9 vertices. Journal of Combinatorial Theory, Series A 15, 3 (Nov. 1973), 270–287.Google ScholarCross Ref
3. Amos Altshuler and Leon Steinberg. 1974. Neighborly combinatorial 3-manifolds with 9 vertices. Discrete Mathematics 8, 2 (April 1974), 113–137. Google ScholarDigital Library
4. Amos Altshuler and Leon Steinberg. 1976. An enumeration of combinatorial 3-manifolds with nine vertices. Discrete Mathematics 16, 2 (Oct. 1976), 91–108.Google ScholarCross Ref
5. Tristan Carrier Baudouin, Jean-Francois Remacle, Emilie Marchandise, Francois Henrotte, and Christophe Geuzaine. 2014. A frontal approach to hex-dominant mesh generation. Advanced Modeling and Simulation in Engineering Sciences 1, 1 (2014), 1. http://amses-journal.springeropen.com/articles/10.1186/2213-7467-1-8Google ScholarCross Ref
6. Steven E. Benzley, Ernest Perry, Karl Merkley, Brett Clark, and Greg Sjaardema. 1995. A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In In Proceedings, 4th International Meshing Roundtable. 179–191.Google Scholar
7. Anders Björner (Ed.). 1999. Oriented matroids (2nd ed ed.). Number v. 46 in Encyclopedia of mathematics and its applications. Cambridge University Press, Cambridge ; New York.Google Scholar
8. Jürgen Bokowski and Jürgen Richter. 1990. On the finding of final polynomials. European Journal of Combinatorics 11, 1 (1990), 21–34.Google ScholarCross Ref
9. Arnaud Botella, Bruno Levy, and Guillaume Caumon. 2016. Indirect unstructured hex-dominant mesh generation using tetrahedra recombination. Computational Geosciences 20, 3 (June 2016), 437–451.Google ScholarCross Ref
10. Tirupathi R. Chandrupatla and Ashok D. Belegundu. 2011. Introduction to finite elements in engineering (4th ed ed.). Prentice Hall, Upper Saddle River, NJ.Google Scholar
11. Jesùs A. De Loera, Jörg Rambau, and Francisco Santos. 2010. Triangulations: structures for algorithms and applications. Number v. 25 in Algorithms and computation in mathematics. Springer, Berlin ; New York. OCLC: ocn646114288. Google ScholarDigital Library
12. Herbert Edelsbrunner and Ernst Peter Mücke. 1990. Simulation of simplicity:a technique to cope with degenerate cases in geometric algorithms. ACM Transactions on Graphics 9, 1 (Jan. 1990), 66–104. Google ScholarDigital Library
13. Xianzhong Fang, Weiwei Xu, Hujun Bao, and Jin Huang. 2016. All-hex meshing using closed-form induced polycube. ACM Transactions on Graphics 35, 4 (July 2016), 1–9. Google ScholarDigital Library
14. Moritz Firsching. 2017. Realizability and inscribability for simplicial polytopes via nonlinear optimization. Mathematical Programming 166, 1–2 (Nov. 2017), 273–295. Google ScholarDigital Library
15. Xifeng Gao, Wenzel Jakob, Marco Tarini, and Daniele Panozzo. 2017. Robust hex-dominant mesh generation using field-guided polyhedral agglomeration. ACM Transactions on Graphics 36, 4 (July 2017), 1–13. Google ScholarDigital Library
16. Ambros Gleixner, Leon Eifler, Tristan Gally, Gerald Gamrath, Patrick Gemander, Robert Lion Gottwald, Gregor Hendel, Christopher Hojny, Thorsten Koch, Matthias Miltenberger, Benjamin Müller, Marc E. Pfetsch, Christian Puchert, Daniel Rehfeldt, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Jan Merlin Viernickel, Stefan Vigerske, Dieter Weninger, Jonas T. Witt, and Jakob Witzig. 2017. The SCIP Optimization Suite 5.0. Technical Report 17–61. ZIB, Takustr.7, 14195 Berlin.Google Scholar
17. Jin Huang, Yiying Tong, Hongyu Wei, and Hujun Bao. 2011. Boundary aligned smooth 3D cross-frame field. ACM Press, 1.Google Scholar
18. Amaury Johnen, Jean-Francois Remacle, and Christophe Geuzaine. 2013. Geometrical validity of curvilinear finite elements. J. Comput. Phys. 233 (Jan. 2013), 359–372. Google ScholarDigital Library
19. Bruno Levy and Yang Liu. 2010. L p Centroidal Voronoi Tessellation and its applications. ACM Transactions on Graphics 29, 4 (July 2010), 1. Google ScholarDigital Library
20. Frank H. Lutz and Thom Sulanke. 2018. The Manifold Page. (2018). http://page.math.tu-berlin.de/~lutz/stellar/ Accessed: 20/08/2018.Google Scholar
21. Max Lyon, David Bommes, and Leif Kobbelt. 2016. HexEx: robust hexahedral mesh extraction. ACM Transactions on Graphics 35, 4 (July 2016), 1–11. Google ScholarDigital Library
22. Brendan D. McKay and Adolfo Piperno. 2014. Practical graph isomorphism, II. Journal of Symbolic Computation 60 (Jan. 2014), 94–112. Google ScholarDigital Library
23. Sia Meshkat and Dafna Talmor. 2000. Generating a mixed mesh of hexahedra, pentahedra and tetrahedra from an underlying tetrahedral mesh. Internat. J. Numer. Methods Engrg. 49, 1–2 (Sept. 2000), 17–30. <17::AID-NME920>3.0.CO;2-UGoogle ScholarCross Ref
24. Jeanne Pellerin, Amaury Johnen, Kilian Verhetsel, and Jean-Francois Remacle. 2018. Identifying combinations of tetrahedra into hexahedra: A vertex based strategy. Computer-Aided Design (June 2018). Code available at: https://www.hextreme.eu/Download/. Accessed 20/08/2018.Google Scholar
25. Julian Pfeifle and Jorg Rambau. 2003. Computing Triangulations Using Oriented Matroids. In Algebra, Geometry and Software Systems, Michael Joswig and Nobuki Takayama (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 49–75.Google Scholar
26. Jörg Rambau. 2003. On a generalization of Schönhardt’s polyhedron. Combinatorial and computational geometry 52 (2003), 510–516.Google Scholar
27. Jean-Francois Remacle, Rajesh Gandham, and Tim Warburton. 2016. GPU accelerated spectral finite elements on all-hex meshes. J. Comput. Phys. 324 (Nov. 2016), 246–257. Google ScholarDigital Library
28. Lars Schewe. 2010. Nonrealizable minimal vertex triangulations of surfaces: showing nonrealizability using oriented matroids and satisfiability solvers. Discrete & Computational Geometry 43, 2 (2010), 289–302. Google ScholarDigital Library
29. Jason F. Shepherd and Chris R. Johnson. 2008. Hexahedral mesh generation constraints. Engineering with Computers 24, 3 (Sept. 2008), 195–213. Google ScholarDigital Library
30. Hang Si. 2015. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Software 41, 2 (Feb. 2015), 1–36. Google ScholarDigital Library
31. Dmitry Sokolov, Nicolas Ray, Lionel Untereiner, and Bruno Levy. 2016. Hexahedral-Dominant Meshing. ACM Transactions on Graphics 35, 5 (June 2016), 1–23. Google ScholarDigital Library
32. Justin Solomon, Amir Vaxman, and David Bommes. 2017. Boundary Element Octahedral Fields in Volumes. ACM Transactions on Graphics 36, 3 (May 2017), 1–16. Google ScholarDigital Library
33. Niklas Sorensson and Niklas Een. 2005. Minisat v1. 13-a sat solver with conflict-clause minimization. SAT 2005, 53 (2005), 1–2.Google Scholar
34. Erke Wang, Thomas Nelson, and Rainer Rauch. 2004. Back to elements-tetrahedra vs. hexahedra. In Proceedings of the 2004 International ANSYS Conference. ANSYS Pennsylvania.Google Scholar
35. Soji Yamakawa and Kenji Shimada. 2003. Fully-automated hex-dominant mesh generation with directionality control via packing rectangular solid cells. International journal for numerical methods in engineering 57, 15 (2003), 2099–2129.Google ScholarCross Ref
36. Gunter M. Ziegler. 1995. Lectures on Polytopes. Graduate Texts in Mathematics, Vol. 152. Springer New York, New York, NY. http://link.springer.com/10.1007/978-1-4613-8431-1Google Scholar