“SurfaceVoronoi: Efficiently Computing Voronoi Diagrams Over Mesh Surfaces with Arbitrary Distance Solvers” by Xin, Wang, Xu, Yan, Chen, et al. …
Conference:
Type(s):
Title:
- SurfaceVoronoi: Efficiently Computing Voronoi Diagrams Over Mesh Surfaces with Arbitrary Distance Solvers
Session/Category Title:
- Distances and Matching
Presenter(s)/Author(s):
Abstract:
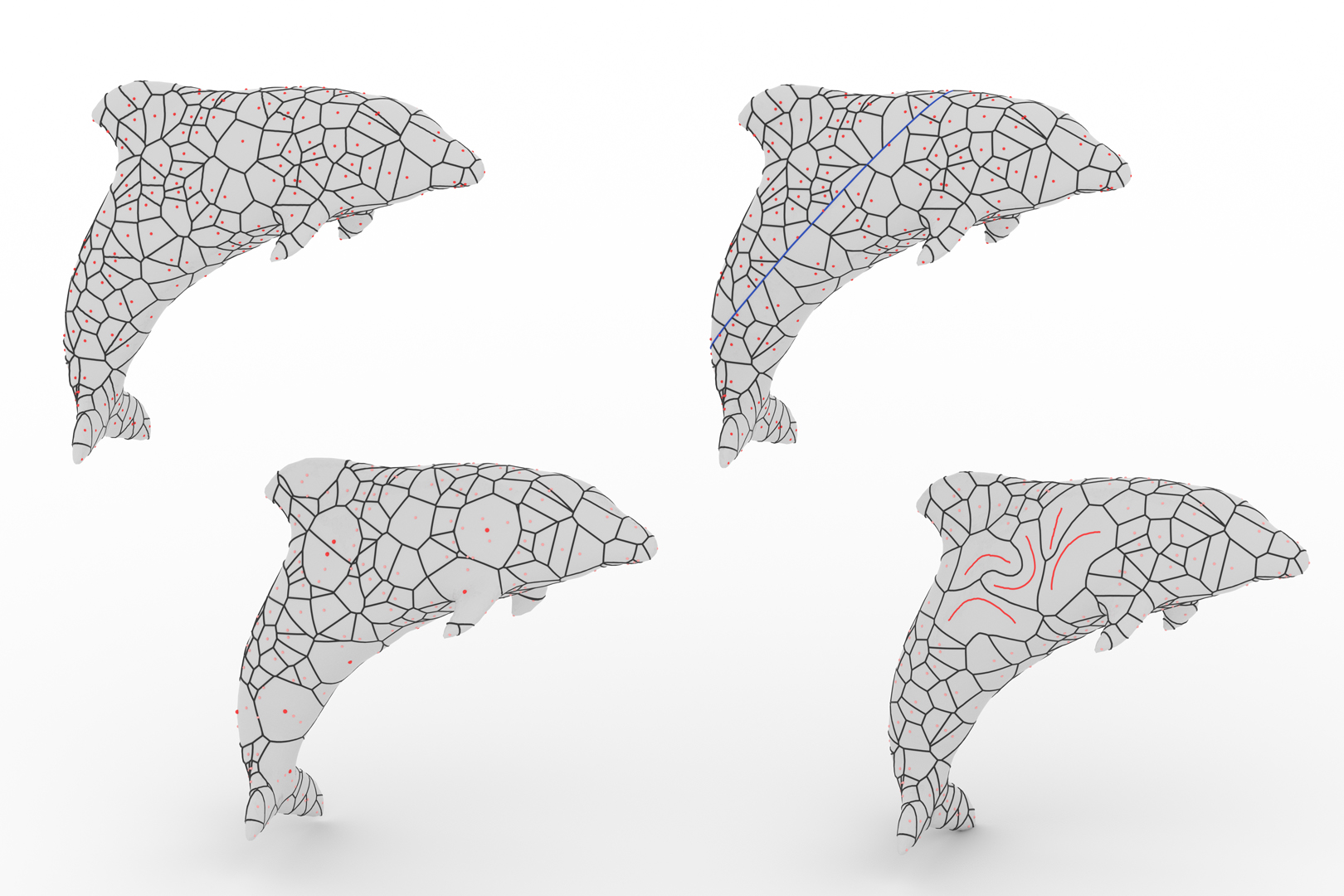
In this paper, we propose to compute Voronoi diagrams over mesh surfaces driven by an arbitrary geodesic distance solver, assuming that the input is a triangle mesh as well as a collection of sites P = {Pi}mi=1 on the surface. We propose two key techniques to solve this problem. First, as the partition is determined by minimizing the m distance fields, each of which rooted at a source site, we suggest keeping one or more distance triples, for each triangle, that may help determine the Voronoi bisectors when one uses a mark-and-sweep geodesic algorithm to predict the multi-source distance field. Second, rather than keep the distance itself at a mesh vertex, we use the squared distance to characterize the linear change of distance field restricted in a triangle, which is proved to induce an exact VD when the base surface reduces to a planar triangle mesh. Specially, our algorithm also supports the Euclidean distance, which can handle thin-sheet models (e.g. leaf) and runs faster than the traditional restricted Voronoi diagram (RVD) algorithm. It is very extensible to deal with various variants of surface-based Voronoi diagrams including (1) surface-based power diagram, (2) constrained Voronoi diagram with curve-type breaklines, and (3) curve-type generators. We conduct extensive experimental results to validate the ability to approximate the exact VD in different distance-driven scenarios.
References:
1. P. Alliez, Éric Colin de Verdière, O. Devillers, and M. Isenburg. 2005. Centroidal Voronoi diagrams for isotropic surface remeshing. Graph. Model. 67 (2005), 204–231.
2. Jie Du, Ying He, Zheng Fang, Wenlong Meng, and Shiqing Xin. 2021a. On the Vertex-oriented Triangle Propagation (VTP) Algorithm: Parallelization and Approximation. Computer-Aided Design 130 (2021), 102943.
3. Xingyi Du, Qingnan Zhou, Nathan Carr, and Tao Ju. 2021b. Boundary-Sampled Halfs-paces: A New Representation for Constructive Solid Modeling. ACM Trans. Graph. 40, 4 (2021).
4. Steven Fortune. 1987. A sweepline algorithm for Voronoi diagrams. Algorithmica 2, 1–4 (1987), 153.
5. Steven Fortune. 1995. Voronoi diagrams and Delaunay triangulations. In Computing in Euclidean geometry. World Scientific, 225–265.
6. Francois Fouss, Alain Pirotte, Jean-michel Renders, and Marco Saerens. 2007. Random-Walk Computation of Similarities between Nodes of a Graph with Application to Collaborative Recommendation. IEEE Transactions on Knowledge and Data Engineering 19, 3 (2007), 355–369.
7. Peter Giblin and Benjamin B Kimia. 2004. A formal classification of 3D medial axis points and their local geometry. IEEE Transactions on Pattern Analysis and Machine Intelligence 26, 2 (2004), 238–251.
8. Peter J Green and Robin Sibson. 1978. Computing Dirichlet tessellations in the plane. The computer journal 21, 2 (1978), 168–173.
9. Philipp Herholz, Felix Haase, and Marc Alexa. 2017. Diffusion Diagrams: Voronoi Cells and Centroids from Diffusion. Computer Graphics Forum 36, 2 (2017), 163–175.
10. Marc Khoury and Jonathan Richard Shewchuk. 2016. Fixed Points of the Restricted Delaunay Triangulation Operator. In 32nd International Symposium on Computational Geometry (SoCG 2016). 47:1–47:15.
11. Ron Kimmel and James A Sethian. 1998. Computing geodesic paths on manifolds. Proceedings of the national academy of Sciences 95, 15 (1998), 8431–8435.
12. Bruno Lévy and Yang Liu. 2010. Lp Centroidal Voronoi Tessellation and its applications. ACM Transactions on Graphics (TOG) 29, 4 (2010), 1–11.
13. Yaron Lipman, Raif M. Rustamov, and Thomas A. Funkhouser. 2010. Biharmonic Distance. ACM Trans. Graph. 29, 3 (2010).
14. Yong-Jin Liu, Zhanqing Chen, and Kai Tang. 2010. Construction of iso-contours, bisectors, and Voronoi diagrams on triangulated surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence 33, 8 (2010), 1502–1517.
15. Yong-Jin Liu, Dian Fan, Chun-Xu Xu, and Ying He. 2017. Constructing intrinsic Delaunay triangulations from the dual of geodesic Voronoi diagrams. ACM Transactions on Graphics (TOG) 36, 2 (2017), 1–15.
16. Joseph SB Mitchell, David M Mount, and Christos H Papadimitriou. 1987. The discrete geodesic problem. SIAM J. Comput. 16, 4 (1987), 647–668.
17. Carsten Moenning and Neil A Dodgson. 2004. Intrinsic point cloud simplification. Proc. 14th GrahiCon 14 (2004), 23.
18. Yipeng Qin, Xiaoguang Han, Hongchuan Yu, Yizhou Yu, and Jianjun Zhang. 2016. Fast and exact discrete geodesic computation based on triangle-oriented wavefront propagation. ACM Transactions on Graphics (TOG) 35, 4 (2016), 1–13.
19. Yipeng Qin, Hongchuan Yu, and Jianjun Zhang. 2017. Fast and Memory-Efficient Voronoi Diagram Construction on Triangle Meshes. Computer Graphics Forum 36, 5, 93–104.
20. Guodong Rong, Miao Jin, and Xiaohu Guo. 2010. Hyperbolic Centroidal Voronoi Tessellation. In Proceedings of the 14th ACM Symposium on Solid and Physical Modeling (Haifa, Israel). ACM, NY, USA, 117–126.
21. Marjorie Senechal. 1993. Spatial tessellations: Concepts and applications of Voronoi diagrams. Science 260, 5111 (1993), 1170–1173.
22. J. A. Sethian. 1999. Fast Marching Methods. SIAM Rev. 41, 2 (1999), 199–235.
23. Michael Ian Shamos and Dan Hoey. 1975. Closest-point problems. In 16th Annual Symposium on Foundations of Computer Science. IEEE, 151–162.
24. Jane Tournois, Pierre Alliez, and Olivier Devillers. 2010. 2D centroidal Voronoi tessellations with constraints. Numerical Mathematics: Theory, Methods and Applications 3, 2 (2010), 212–222.
25. Pengfei Wang, Shiqing Xin, Changhe Tu, Dongming Yan, Yuanfeng Zhou, and Caiming Zhang. 2020. Robustly computing restricted Voronoi diagrams (RVD) on thin-plate models. Computer Aided Geometric Design (2020), 101848.
26. Xiaoning Wang, Xiang Ying, Yong-Jin Liu, Shi-Qing Xin, Wenping Wang, Xianfeng Gu, Wolfgang Mueller-Wittig, and Ying He. 2015. Intrinsic computation of centroidal Voronoi tessellation (CVT) on meshes. Computer-Aided Design 58 (2015), 51–61.
27. Shi-Qing Xin and Guo-Jin Wang. 2009. Improving Chen and Han’s algorithm on the discrete geodesic problem. ACM Transactions on Graphics (TOG) 28, 4 (2009), 1–8.
28. Chunxu Xu, Yong-Jin Liu, Qian Sun, Jinyan Li, and Ying He. 2014. Polyline-sourced Geodesic Voronoi Diagrams on Triangle Meshes. Computer Graphics Forum 33, 7, 161–170.
29. Dong-Ming Yan, Guanbo Bao, Xiaopeng Zhang, and Peter Wonka. 2014. Low-resolution remeshing using the localized restricted Voronoi diagram. IEEE transactions on visualization and computer graphics 20, 10 (2014), 1418–1427.
30. Dong-Ming Yan, Bruno Lévy, Yang Liu, Feng Sun, and Wenping Wang. 2009. Isotropic remeshing with fast and exact computation of restricted Voronoi diagram. Computer graphics forum 28, 5, 1445–1454.
31. Dong-Ming Yan, Wenping Wang, Bruno Lévy, and Yang Liu. 2013. Efficient computation of clipped Voronoi diagram for mesh generation. Computer-Aided Design 45, 4 (2013), 843–852.
32. Rhaleb Zayer, Daniel Mlakar, Markus Steinberger, and Hans-Peter Seidel. 2018. Layered Fields for Natural Tessellations on Surfaces. ACM Trans. Graph. 37, 6 (2018).