“Stochastic Computation of Barycentric Coordinates”
Conference:
Type(s):
Title:
- Stochastic Computation of Barycentric Coordinates
Presenter(s)/Author(s):
Abstract:
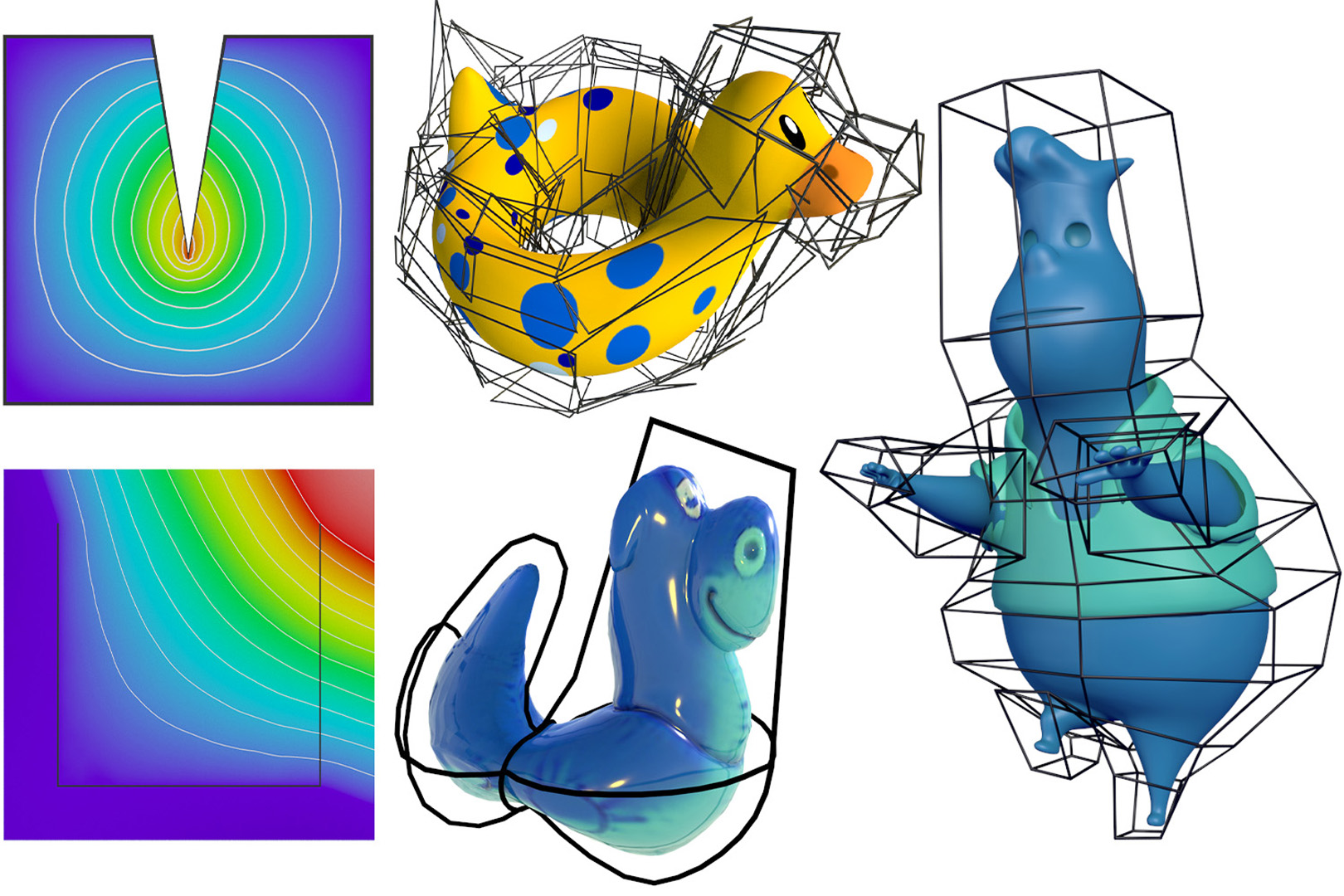
We introduce an approach for computing barycentric coordinates inside and outside a cage domain using only cage queries such as closest points and ray intersections. We show that this stochastic construction reproduces existing barycentric coordinates, e.g., harmonic and (positive) mean-value coordinates, while seamlessly accommodating a variety of cage representations.
References:
[1]
Alexander Belyaev. 2006. On Transfinite Barycentric Coordinates. In Symposium on Geometry Processing.
[2]
Mirela Ben-Chen, Ofir Weber, and Craig Gotsman. 2009. Variational Harmonic Maps for Space Deformation. ACM Trans. Graph. 28, 3, Article 34 (2009).
[3]
Ilia Binder and Mark Braverman. 2012. The rate of convergence of the Walk on Spheres Algorithm. Geometric and Functional Analysis 22 (aug 2012), 558–587.
[4]
Max Budninskiy, Beibei Liu, Yiying Tong, and Mathieu Desbrun. 2016. Power Coordinates: A Geometric Construction of Barycentric Coordinates on Convex Polytopes. ACM Trans. Graph. 35, 6, Article 241 (2016).
[5]
Qingjun Chang, Chongyang Deng, and Kai Hormann. 2023. Maximum likelihood coordinates. Computer Graphics Forum 42, 5 (Aug. 2023), Article e14908, 13 pages. Proceedings of SGP.
[6]
Jiong Chen, Fernando De Goes, and Mathieu Desbrun. 2023. Somigliana Coordinates: An Elasticity-Derived Approach for Cage Deformation. In ACM SIGGRAPH Conference Proceedings. Article 52, 8 pages.
[7]
Xiao-Song Chen, Chen-Feng Li, Geng-Chen Cao, Yun-Tao Jiang, and Shi-Min Hu. 2020. A Moving Least Square Reproducing Kernel Particle Method for Unified Multiphase Continuum Simulation. ACM Trans. Graph. 39, 6, Article 176 (nov 2020).
[8]
Fernando de Goes, Andrew Butts, and Mathieu Desbrun. 2020. Discrete Differential Operators on Polygonal Meshes. ACM Trans. Graph. 39, 4, Article 110 (aug 2020).
[9]
Mathieu Desbrun, Mark Meyer, Peter Schr?der, and Alan H. Barr. 1999. Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. 317–324.
[10]
Ana Dodik, Oded Stein, Vincent Sitzmann, and Justin Solomon. 2023. Variational Barycentric Coordinates. ACM Trans. Graph. 42, 6, Article 255 (2023), 16 pages.
[11]
Michael S. Floater. 2003. Mean Value Coordinates. Comput. Aided Geom. Design 20, 1 (2003), 19–27.
[12]
Michael S. Floater. 2015. Generalized barycentric coordinates and applications. Acta Numerica 24 (2015), 161–214.
[13]
Michael S. Floater, Kai Hormann, and G?za K?s. 2006. A general construction of barycentric coordinates over convex polygons. Advances in Computational Mathematics 24 (2006), 311–331.
[14]
Michael S. Floater, G?za K?s, and Martin Reimers. 2005. Mean value coordinates in 3D. Computer Aided Geometric Design 22, 7 (2005), 623–631.
[15]
Thomas-Peter Fries and Hermann G. Matthies. 2004. Classification and Overview of Meshfree Methods. Informatik-Berichte der Technischen Universit?t Braunschweig 2003-03 (2004).
[16]
William J. Gordon and James A. Wixom. 1974. Pseudo-Harmonic Interpolation on Convex Domains. SIAM J. Numer. Anal. 11, 5 (1974), 909–933.
[17]
Kai Hormann and Michael S. Floater. 2006. Mean Value Coordinates for Arbitrary Planar Polygons. ACM Trans. Graph. 25, 4 (oct 2006), 1424–1441.
[18]
Kai Hormann and N. Sukumar. 2008. Maximum Entropy Coordinates for Arbitrary Polytopes. In Symp. Geo. Proc. 1513–1520.
[19]
Kai Hormann and N. Sukumar. 2017. Generalized barycentric coordinates in computer graphics and computational mechanics. CRC press.
[20]
Pushkar Joshi, Mark Meyer, Tony DeRose, Brian Green, and Tom Sanocki. 2007. Harmonic Coordinates for Character Articulation. ACM Trans. Graph. 26, 3, Article 71 (2007).
[21]
Tao Ju, Scott Schaefer, and Joe Warren. 2005. Mean Value Coordinates for Closed Triangular Meshes. ACM Trans. Graph. 24, 3 (jul 2005), 561–566.
[22]
David Levin. 1998. The approximation power of moving least-squares. Math. Comp. 67, 224 (oct 1998), 1517–1531.
[23]
Yaron Lipman, Johannes Kopf, Daniel Cohen-Or, and David Levin. 2007. GPU-assisted Positive Mean Value Coordinates for Mesh Deformations. In Symposium on Geometry Processing.
[24]
Yaron Lipman, David Levin, and Daniel Cohen-Or. 2008. Green Coordinates. ACM Trans. Graph. 27, 3 (2008), 1–10.
[25]
Wing-Kam Liu, Sukky Jun, and Yifei Zhang. 1995. Reproducing kernel particle methods. Int. J. Num. Meth. Fluids 20, 8–9 (1995), 1081–1106.
[26]
Wing-Kam Liu, Shaofan Li, and Ted Belytschko. 1997. Moving least-square reproducing kernel methods (I) Methodology and convergence. Computer Methods in Applied Mechanics and Engineering 143, 1 (1997), 113–154.
[27]
Abhishek Madan and David I. W. Levin. 2022. Fast Evaluation of Smooth Distance Constraints on Co-Dimensional Geometry. ACM Trans. Graph. 41, 4, Article 68 (jul 2022), 17 pages.
[28]
Josiah Manson and Scott Schaefer. 2010. Moving Least Squares Coordinates. Computer Graphics Forum 29, 5 (2010), 1517–1524.
[29]
Sebastian Martin, Peter Kaufmann, Mario Botsch, Martin Wicke, and Markus Gross. 2008. Polyhedral Finite Elements Using Harmonic Basis Functions. Computer Graphics Forum 27, 5 (2008), 1521–1529.
[30]
Mark Meyer, Alan Barr, Haeyoung Lee, and Mathieu Desbrun. 2002. Generalized Barycentric Coordinates on Irregular Polygons. J. Graph. Tools 7, 1 (2002), 13–22.
[31]
Bailey Miller, Rohan Sawhney, Keenan Crane, and Ioannis Gkioulekas. 2023. Boundary Value Caching for Walk on Spheres. ACM Trans. Graph. 42, 4 (2023).
[32]
August Ferdinand M?bius. 1827. Der Barycentrische Calcul : ein neues H?lfsmittel zur analytischen Behandlung der Geometrie. Leipzig, Verlag von Johann Ambrosius Barth.
[33]
Mervin E. Muller. 1956. Some Continuous Monte Carlo Methods for the Dirichlet Problem. The Annals of Mathematical Statistics 27, 3 (1956), 569–589.
[34]
James Reinders. 2007. Intel Threading Building Blocks. O’Reilly & Associates, Inc.
[35]
Alexander Reshetov. 2019. Cool Patches: A Geometric Approach to Ray/Bilinear Patch Intersections. 95–109 pages.
[36]
Rohan Sawhney and Keenan Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 39, 4 (2020).
[37]
Nicholas Sharp and Keenan Crane. 2020. A Laplacian for Nonmanifold Triangle Meshes. Computer Graphics Forum (SGP) 39, 5 (2020).
[38]
Nicholas Sharp and Alec Jacobson. 2022. Spelunking the Deep: Guaranteed Queries on General Neural Implicit Surfaces via Range Analysis. ACM Trans. Graph. 41, 4, Article 107 (jul 2022), 16 pages.
[39]
Side Effects. 2024. Houdini Engine. http://www.sidefx.com.
[40]
Ryusuke Sugimoto, Terry Chen, Yiti Jiang, Christopher Batty, and Toshiya Hachisuka. 2023. A Practical Walk-on-Boundary Method for Boundary Value Problems. ACM Trans. Graph. 42, 4, Article 81 (jul 2023), 16 pages.
[41]
Jean-Marc Thiery and Tamy Boubekeur. 2022. Green Coordinates for Triquad Cages in 3D. In SIGGRAPH Asia Conference Papers. Article 38.
[42]
Jean-Marc Thiery, Pooran Memari, and Tamy Boubekeur. 2018. Mean Value Coordinates for Quad Cages in 3D. ACM Trans. Graph. 37, 6, Article 229 (2018).
[43]
Joe Warren, Scott Schaefer, Anil Hirani, and Mathieu Desbrun. 2007. Barycentric Coordinates for Convex Sets. Adv. Comput. Math. 27, 3 (2007), 319–338.
[44]
Ofir Weber. 2017. Planar Shape Deformation. In Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics, Kai Hormann and N. Sukumar (Eds.). CRC Press, Chapter 7, 109–133.
[45]
Ofir Weber, Mirela Ben-Chen, and Craig Gotsman. 2009. Complex Barycentric Coordinates with Applications to Planar Shape Deformation. Comput. Graph. Forum 28, 2 (2009).
[46]
Ofir Weber and Craig Gotsman. 2010. Controllable Conformal Maps for Shape Deformation and Interpolation. In ACM SIGGRAPH Proceedings. Article 78.
[47]
Lukas Westhofen, Stefan Jeske, and Jan Bender. 2023. A Comparison of Linear Consistent Correction Methods for First-Order SPH Derivatives. Proc. ACM Comput. Graph. Interact. Tech. 6, 3, Article 48 (2023), 20 pages.
[48]
Zhipei Yan and Scott Schaefer. 2019. A Family of Barycentric Coordinates for Co-Dimension 1 Manifolds with Simplicial Facets. Computer Graphics Forum 38, 5 (2019), 75–83.
[49]
Juyong Zhang, Bailin Deng, Zishun Liu, Giuseppe Patan?, Sofien Bouaziz, Kai Hormann, and Ligang Liu. 2014. Local Barycentric Coordinates. ACM Trans. Graph. 33, 6, Article 188 (nov 2014), 12 pages.