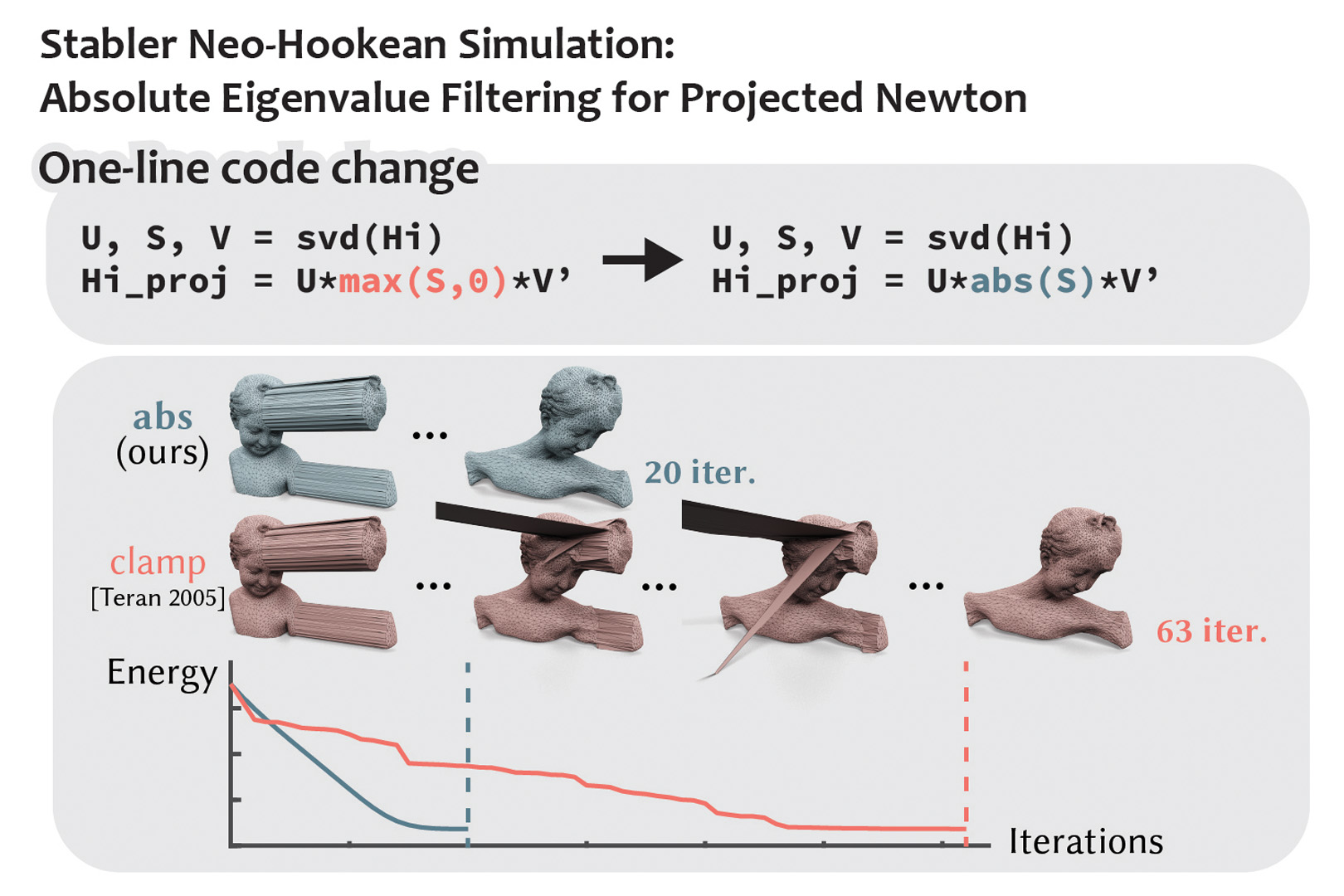
“Stabler Neo-Hookean Simulation: Absolute Eigenvalue Filtering for Projected Newton” by Chen, Liu, Levin, Zheng and Jacobson
Conference:
Type(s):
Title:
- Stabler Neo-Hookean Simulation: Absolute Eigenvalue Filtering for Projected Newton
Presenter(s)/Author(s):
Abstract:
We introduce a novel eigenvalue filtering strategy for projected Newton’s method to stabilize the optimization of Neo-Hookean energy under high Poisson’s ratios (near 0.5) and large initial volume change. Our method only requires a single line of code change, while achieving significant improvement in both stability and convergence speed.
References:
[1]
Xiang Chen, Changxi Zheng, Weiwei Xu, and Kun Zhou. 2014. An Asymptotic Numerical Method for Inverse Elastic Shape Design. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2014) 33, 4 (Aug. 2014).
[2]
Yann N. Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, and Yoshua Bengio. 2014. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Proceedings of the 27th International Conference on Neural Information Processing Systems – Volume 2 (Montreal, Canada) (NIPS?14). MIT Press, Cambridge, MA, USA, 2933?2941.
[3]
Xiao-Ming Fu and Yang Liu. 2016. Computing inversion-free mappings by simplex assembly. ACM Trans. Graph. 35, 6 (2016), 216:1?216:12.
[4]
P.E. Gill, W. Murray, and M.H. Wright. 1981. Practical Optimization. Academic Press. https://books.google.com/books?id=xUzvAAAAMAAJ
[5]
Yixin Hu, Qingnan Zhou, Xifeng Gao, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2018. Tetrahedral Meshing in the Wild. ACM Trans. Graph. 37, 4, Article 60 (July 2018), 14 pages. https://doi.org/10.1145/3197517.3201353
[6]
Alec Jacobson, Daniele Panozzo, 2018. libigl: A simple C++ geometry processing library. https://libigl.github.io/.
[7]
Theodore Kim and David Eberle. 2022. Dynamic Deformables: Implementation and Production Practicalities (Now with Code!). In ACM SIGGRAPH 2022 Courses (Vancouver, British Columbia, Canada) (SIGGRAPH ?22). Association for Computing Machinery, New York, NY, USA, Article 7, 259 pages. https://doi.org/10.1145/3532720.3535628
[8]
Lei Lan, Minchen Li, Chenfanfu Jiang, Huamin Wang, and Yin Yang. 2023. Second-Order Stencil Descent for Interior-Point Hyperelasticity. ACM Trans. Graph. 42, 4, Article 108 (jul 2023), 16 pages. https://doi.org/10.1145/3592104
[9]
Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, and Danny M. Kaufman. 2020. Incremental Potential Contact: Intersection- and Inversion-free Large Deformation Dynamics. ACM Trans. Graph. (SIGGRAPH) 39, 4, Article 49 (2020).
[10]
Huancheng Lin, Floyd M. Chitalu, and Taku Komura. 2022. Isotropic ARAP Energy Using Cauchy-Green Invariants. ACM Trans. Graph. 41, 6, Article 275 (nov 2022), 14 pages. https://doi.org/10.1145/3550454.3555507
[11]
Tiantian Liu, Sofien Bouaziz, and Ladislav Kavan. 2017. Quasi-Newton Methods for Real-Time Simulation of Hyperelastic Materials. ACM Transactions on Graphics (TOG) 36, 3 (2017), 23.
[12]
Andreas Longva, Fabian L?schner, Jos? Antonio Fern?ndez-Fern?ndez, Egor Larionov, Uri M. Ascher, and Jan Bender. 2023. Pitfalls of Projection: A study of Newton-type solvers for incremental potentials. arxiv:2311.14526
[13]
Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-based elastic materials. In ACM SIGGRAPH 2011 Papers (Vancouver, British Columbia, Canada) (SIGGRAPH ?11). Association for Computing Machinery, New York, NY, USA, Article 72, 8 pages. https://doi.org/10.1145/1964921.1964967
[14]
Matthias M?ller, Julie Dorsey, Leonard McMillan, Robert Jagnow, and Barbara Cutler. 2002. Stable Real-Time Deformations. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (San Antonio, Texas) (SCA ?02). Association for Computing Machinery, New York, NY, USA, 49?54. https://doi.org/10.1145/545261.545269
[15]
Jorge Nocedal and Stephen J. Wright. 2006. Numerical Optimization. (2006).
[16]
Raymond W Ogden. 1997. Non-linear elastic deformations. Courier Corporation.
[17]
Santiago Paternain, Aryan Mokhtari, and Alejandro Ribeiro. 2019. A Newton-Based Method for Nonconvex Optimization with Fast Evasion of Saddle Points. SIAM Journal on Optimization 29, 1 (2019), 343?368. https://doi.org/10.1137/17M1150116
[18]
Guillaume Picinbono, Herv? Delingette, and Nicholas Ayache. 2004. Real-Time Large Displacement Elasticity for Surgery Simulation: Non-linear Tensor-Mass Model. MICCAI 1935, CH41?CH41. https://doi.org/10.1007/978-3-540-40899-4_66
[19]
Ralph Tyrell Rockafellar. 1970. Convex Analysis. Princeton University Press, Princeton. https://doi.org/
[20]
Patrick Schmidt, Janis Born, David Bommes, Marcel Campen, and Leif Kobbelt. 2022. TinyAD: Automatic Differentiation in Geometry Processing Made Simple. Computer Graphics Forum 41, 5 (2022).
[21]
Anna Shtengel, Roi Poranne, Olga Sorkine-Hornung, Shahar Z. Kovalsky, and Yaron Lipman. 2017. Geometric Optimization via Composite Majorization. ACM Trans. Graph. 36, 4, Article 38 (jul 2017), 11 pages. https://doi.org/10.1145/3072959.3073618
[22]
Breannan Smith, Fernando De Goes, and Theodore Kim. 2018. Stable Neo-Hookean Flesh Simulation. ACM Trans. Graph. 37, 2, Article 12 (mar 2018), 15 pages. https://doi.org/10.1145/3180491
[23]
Breannan Smith, Fernando De Goes, and Theodore Kim. 2019. Analytic Eigensystems for Isotropic Distortion Energies. ACM Trans. Graph. 38, 1, Article 3 (feb 2019), 15 pages. https://doi.org/10.1145/3241041
[24]
Jason Smith and Scott Schaefer. 2015. Bijective parameterization with free boundaries. ACM Trans. Graph. 34, 4, Article 70 (jul 2015), 9 pages.
[25]
Joseph Teran, Eftychios Sifakis, Geoffrey Irving, and Ronald Fedkiw. 2005. Robust Quasistatic Finite Elements and Flesh Simulation. In ACM/Eurographics Symposium on Computer Animation (SCA), K. Anjyo and P. Faloutsos (Eds.). 181?190. http://graphics.cs.wisc.edu/Papers/2005/TSIF05
[26]
Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv preprint arXiv:1605.04797 (2016).