“Robust Containment Queries Over Collections of Rational Parametric Curves via Generalized Winding Numbers”
Conference:
Type(s):
Title:
- Robust Containment Queries Over Collections of Rational Parametric Curves via Generalized Winding Numbers
Presenter(s)/Author(s):
Abstract:
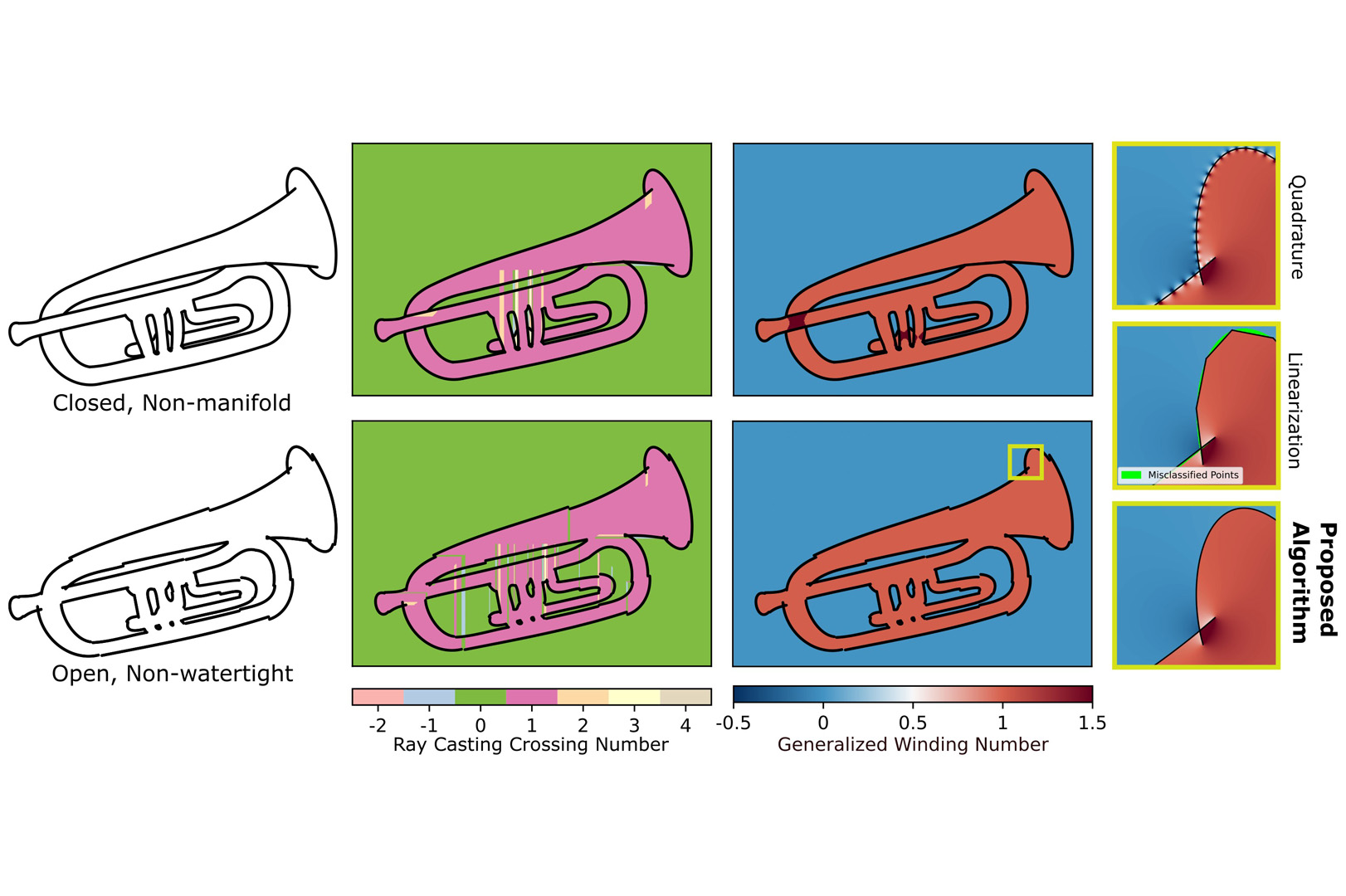
We extend the theory of generalized winding numbers to unstructured collections of rational parametric curves with a numerically stable algorithm, thereby allowing for robust and accurate containment classifications at arbitrary locations for non-watertight and self-intersecting shapes.
References:
[1]
P. Asente, M. Schuster, and T. Pettit. 2007. Dynamic planar map illustration. ACM Transactions on Graphics 26, 3 (July 2007), 30:1–10.
[2]
A. Balu, M. R. Rajanna, J. Khristy, F. Xu, A. Krishnamurthy, and M.-C. Hsu. 2023. Direct immersogeometric fluid flow and heat transfer analysis of objects represented by point clouds. Computer Methods in Applied Mechanics and Engineering 404 (Feb. 2023), 115742.
[3]
G. Barill, N. Dickson, R. Schmidt, D. I. W. Levin, and A. Jacobson. 2018. Fast Winding Numbers for Soups and Clouds. ACM Transactions on Graphics 37, 4, Article 43 (July 2018), 12 pages.
[4]
A. J. Barlow, P.-H. Maire, W. J. Rider, R. N. Rieben, and M. J. Shashkov. 2016. Arbitrary Lagrangian-Eulerian methods for modeling high-speed compressible multimaterial flows. J. Comput. Phys. 322 (2016), 603–665.
[5]
S. Bischoff, D. Pavic, and L. Kobbelt. 2005. Automatic restoration of polygon models. ACM Transactions on Graphics 24, 4 (Oct. 2005), 1332–1352.
[6]
A. Capps, R. Carson, B. Corbett, N. Elliott, J. Essman, B. Gunney, B. Han, C. Harrison, R. Hornung, M. Larsen, A. Moody, E. Pauli, R. Settgast, L. Taylor, K. Weiss, C. White, B. Whitlock, M. Yang, and G. Zagaris. 2017–2024. Axom: CS infrastructure components for HPC applications. https://github.com/llnl/axom.
[7]
P. C. P. Carvalho and P. R. Cavalcanti. 1995. II.2 – Point in Polyhedron Testing Using Spherical Polygons. In Graphics Gems V, A. W. Paeth (Ed.). Academic Press, Boston, 42–49.
[8]
H. Edelsbrunner and E. P. M?cke. 1990. Simulation of simplicity: A technique to cope with degenerate cases in geometric algorithms. ACM Trans. Graph. 9, 1 (Jan. 1990), 66–104.
[9]
A. Efremov, V. Havran, and H.-P. Seidel. 2005. Robust and Numerically Stable B?zier Clipping Method for Ray Tracing NURBS Surfaces. In Proceedings of the 21st Spring Conference on Computer Graphics (Budmerice, Slovakia) (SCCG ’05). Association for Computing Machinery, New York, NY, USA, 127–135.
[10]
G. E. Farin. 2001. Curves and surfaces for CAGD: A practical guide. Morgan Kaufmann.
[11]
D. Gunderman. 2021. High-Order Spatial Discretization and Numerical Integration Schemes for Curved Geometries. Ph. D. Dissertation. Department of Applied Mathematics, University of Colorado Boulder.
[12]
D. Gunderman, K. Weiss, and J. A. Evans. 2020. Spectral mesh-free quadrature for planar regions bounded by rational parametric curves. Computer-Aided Design 130 (2020).
[13]
E. Haines. 1994. I.4. – Point in Polygon Strategies. In Graphics Gems, P. S. Heckbert (Ed.). Academic Press, 24–46.
[14]
C.W. Hirt, A. A. Amsden, and J. L. Cook. 1974. An Arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 14, 3 (1974), 227–253.
[15]
K. Hormann and A. Agathos. 2001. The point in polygon problem for arbitrary polygons. Computational Geometry 20, 3 (2001), 131–144.
[16]
A. Jacobson, L. Kavan, and O. Sorkine. 2013. Robust Inside-Outside Segmentation using Generalized Winding Numbers. ACM Trans. Graph. 32, 4 (2013), 1–12.
[17]
M. J. Kilgard. 2020. Polar stroking: New theory and methods for stroking paths. ACM Transactions on Graphics 39, 4 (Aug. 2020), 145:1–15.
[18]
L. Klinteberg and A. H. Barnett. 2020. Accurate quadrature of nearly singular line integrals in two and three dimensions by singularity swapping. BIT Numerical Mathematics 61 (07 2020), 1–36.
[19]
Y. L. Ma and W. T. Hewitt. 2003. Point inversion and projection for NURBS curve and surface: Control polygon approach. Computer Aided Geometric Design 20, 2 (2003), 79–99.
[20]
B. Marussig and T. Hughes. 2017. A Review of Trimming in Isogeometric Analysis: Challenges, Data Exchange and Simulation Aspects. Archives of Computational Methods in Engineering 25 (06 2017), 1–69.
[21]
A. McAdams, Y. Zhu, A. Selle, M. Empey, R. Tamstorf, J. Teran, and E. Sifakis. 2011. Efficient Elasticity for Character Skinning with Contact and Collisions. ACM Trans. Graph. 30, 4, Article 37 (July 2011), 12 pages.
[22]
A. A. Mezentsev and T. Woehler. 1999. Methods and Algorithms of Automated CAD Repair for Incremental Surface Meshing. In IMR. Citeseer, 299–309.
[23]
T. Nishita, T. W. Sederberg, and M. Kakimoto. 1990. Ray Tracing Trimmed Rational Surface Patches. SIGGRAPH Comput. Graph. 24, 4 (sep 1990), 337–345.
[24]
F. S. Nooruddin and G. Turk. 2003. Simplification and repair of polygonal models using volumetric techniques. IEEE Transactions on Visualization and Computer Graphics 9, 2 (2003), 191–205.
[25]
A. Orzan, A. Bousseau, H. Winnem?ller, P. Barla, J. Thollot, and D. Salesin. 2008. Diffusion Curves: A Vector Representation for Smooth-Shaded Images. ACM Transactions on Graphics 27, 3 (Aug. 2008), 92:1–8.
[26]
M. A. Park, R. Haimes, N. J. Wyman, P. A. Baker, and A. Loseille. 2021. Boundary Representation Tolerance Impacts on Mesh Generation and Adaptation. In AIAA AVIATION 2021 FORUM.
[27]
N. Patrikalakis and T. Maekawa. 2010. Shape Interrogation for Computer Aided Design and Manufacturing.
[28]
L. Piegl and W. Tiller. 1996. The NURBS book. Springer Science & Business Media.
[29]
R. Sawhney and K. Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Transactions on Graphics 39, 4 (2020).
[30]
T. W. Sederberg, G. T. Finnigan, X. Li, H. Lin, and H. Ipson. 2008. Watertight trimmed NURBS. ACM Transactions on Graphics 27, 3 (Aug. 2008), 1–8.
[31]
T. W. Sederberg and T. Nishita. 1990. Curve intersection using B?zier clipping. Computer-Aided Design 22, 9 (1990), 538–549.
[32]
S. Sell?n and A. Jacobson. 2022. Stochastic Poisson Surface Reconstruction. ACM Transactions on Graphics 41, 6, Article 227 (Nov. 2022), 12 pages.
[33]
R. Sevilla, S. Fern?ndez-M?ndez, and A. Huerta. 2008. NURBS-enhanced finite element method for Euler equations. International Journal for Numerical Methods in Fluids 57, 9 (2008), 1051–1069.
[34]
R. Sevilla, S. Fern?ndez-M?ndez, and A. Huerta. 2011. 3D NURBS-enhanced finite element method (NEFEM). Internat. J. Numer. Methods Engrg. 88, 2 (2011), 103–125.
[35]
M. Shimrat. 1962. Algorithm 112: Position of Point Relative to Polygon. Commun. ACM 5, 8 (Aug. 1962), 434.
[36]
A. Sommariva and M. Vianello. 2022. inRS: Implementing the indicator function of NURBS-shaped planar domains. Applied Mathematics Letters 130 (2022), 108026.
[37]
D. C. Thomas, M. A. Scott, J. A. Evans, K. Tew, and E. J. Evans. 2015. B?zier projection: A unified approach for local projection and quadrature-free refinement and coarsening of NURBS and T-splines with particular application to isogeometric design and analysis. Computer Methods in Applied Mechanics and Engineering 284 (2015), 55–105. Isogeometric Analysis Special Issue.
[38]
P. Trettner, J. Nehring-Wirxel, and L. Kobbelt. 2022. EMBER: Exact Mesh Booleans via Efficient & Robust Local Arrangements. ACM Trans. Graph. 41, 4, Article 39 (July 2022), 15 pages.
[39]
K. Weiss, G. Zagaris, R. Rieben, and A. Cook. 2016. Spatially accelerated shape embedding in multimaterial simulations. In Proceedings 25th International Meshing Roundtable (IMR ’16), S. Canann (Ed.). Washington, D.C.
[40]
S. Zellmann, D. Seifried, N. Morrical, I. Wald, W. Usher, J. P. Law-Smith, S. Walch-Gassner, and A. Hinkenjann. 2022. Point Containment Queries on Ray-Tracing Cores for AMR Flow Visualization. Computing in Science & Engineering 24, 02 (March 2022), 40–51.