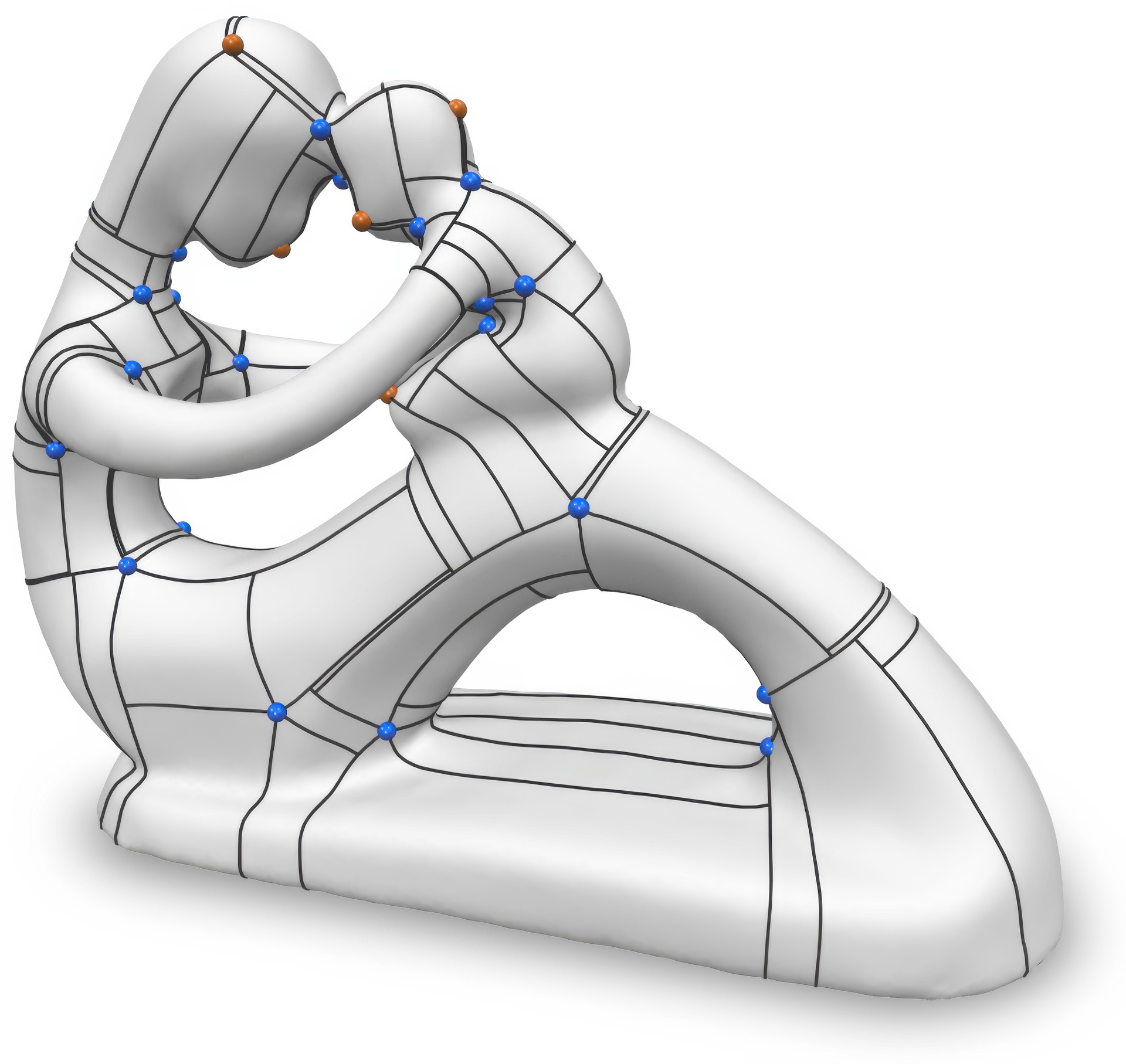
“Quantized global parametrization”
Conference:
Type(s):
Title:
- Quantized global parametrization
Session/Category Title:
- Mappings and Parameterizations
Presenter(s)/Author(s):
Abstract:
Global surface parametrization often requires the use of cuts or charts due to non-trivial topology. In recent years a focus has been on so-called seamless parametrizations, where the transition functions across the cuts are rigid transformations with a rotation about some multiple of 90°. Of particular interest, e.g. for quadrilateral meshing, paneling, or texturing, are those instances where in addition the translational part of these transitions is integral (or more generally: quantized). We show that finding not even the optimal, but just an arbitrary valid quantization (one that does not imply parametric degeneracies), is a complex combinatorial problem. We present a novel method that allows us to solve it, i.e. to find valid as well as good quality quantizations. It is based on an original approach to quickly construct solutions to linear Diophantine equation systems, exploiting the specific geometric nature of the parametrization problem. We thereby largely outperform the state-of-the-art, sometimes by several orders of magnitude.
References:
1. Bommes, D., Vossemer, T., and Kobbelt, L. 2008. Quadrangular parameterization for reverse engineering. Mathematical Methods for Curves and Surfaces, 55–69.
2. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. In Proc. SIGGRAPH 2009, 1–10.
3. Bommes, D., Lévy, B., Pietroni, N., Puppo, E., Silva, C., Tarini, M., and Zorin, D. 2013. Quad-mesh generation and processing: A survey. Computer Graphics Forum 32, 6, 51–76.
4. Bommes, D., Campen, M., Ebke, H.-C., Alliez, P., and Kobbelt, L. 2013. Integer-grid maps for reliable quad meshing. In Proc. SIGGRAPH 2013, 98:1–98:12.
5. Campen, M., and Kobbelt, L. 2014. Dual strip weaving: Interactive design of quad layouts using elastica strips. In Proc. SIGGRAPH Asia 2014, 183:1–183:10.
6. Campen, M., and Kobbelt, L. 2014. Quad layout embedding via aligned parameterization. Computer Graphics Forum 33, 8, 69–81.
7. Campen, M., Bommes, D., and Kobbelt, L. 2012. Dual loops meshing: quality quad layouts on manifolds. In Proc. SIGGRAPH 2012, 110:1–110:11.
8. Colin de Verdière, E., and Lazarus, F. 2005. Optimal system of loops on an orientable surface. Discrete & Computational Geometry 33, 3, 507–534.
9. Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and Hart, J. C. 2006. Spectral surface quadrangulation. In Proc. SIGGRAPH 2006, 1057–1066.
10. Dumitrescu, A., Rote, G., and Tth, C. 2013. Monotone paths in planar convex subdivisions and polytopes. In Discrete Geometry and Optimization, vol. 69 of Fields Institute Communications. Springer, 79–104.
11. Ebke, H.-C., Bommes, D., Campen, M., and Kobbelt, L. 2013. Qex: Robust quad mesh extraction. In Proc. SIGGRAPH Asia 2013, 168:1–168:10.
12. Ebke, H.-C., Campen, M., Bommes, D., and Kobbelt, L. 2014. Level-of-detail quad meshing. In Proc. SIGGRAPH Asia 2014, 184:1–184:11.
13. Eck, M., and Hoppe, H. 1996. Automatic reconstruction of B-spline surfaces of arbitrary topological type. In Proc. SIGGRAPH 96, 325–334.
14. Eppstein, D., Goodrich, M. T., Kim, E., and Tamstorf, R. 2008. Motorcycle Graphs: Canonical Quad Mesh Partitioning. Computer Graphics Forum 27, 5, 1477–1486.
15. Floater, M. S., and Hormann, K. 2005. Surface parameterization: a tutorial and survey. In Advances in Multiresolution for Geometric Modelling. Springer, 157–186.
16. Gu, X., Gortler, S. J., and Hoppe, H. 2002. Geometry images. In Proc. SIGGRAPH ’02, 355–361.
17. Guskov, I., Vidimce, K., Sweldens, W., and Schröder, P. 2000. Normal meshes. In Proc. SIGGRAPH 2000, 95–102.
18. Jiang, T., Fang, X., Huang, J., Bao, H., Tong, Y., and Desbrun, M. 2015. Frame field generation through metric customization. ACM Trans. Graph. 34, 4.
19. Johnson, D. B. 1975. Finding all the elementary circuits of a directed graph. SIAM J. Comput. 4, 1, 77–84.
20. Jucovič, E., and Trenkler, M. 1973. A theorem on the structure of cell-decompositions of orientable 2-manifolds. Mathematika 20, 63–82.
21. Kälberer, F., Nieser, M., and Polthier, K. 2007. Quadcover – surface parameterization using branched coverings. Computer Graphics Forum 26, 3, 375–384.
22. Khodakovsky, A., Litke, N., and Schröder, P. 2003. Globally smooth parameterizations with low distortion. ACM Trans. Graph. 22, 3, 350–357.
23. Lévy, B., Petitjean, S., Ray, N., and Maillot, J. 2002. Least squares conformal maps for automatic texture atlas generation. ACM Trans. Graph. 21, 3, 362–371.
24. Li, E., Lévy, B., Zhang, X., Che, W., Dong, W., and Paul, J.-C. 2011. Meshless quadrangulation by global parameterization. Computers & Graphics, 992–1000.
25. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. In Proc. SIGGRAPH 2012, 108:1–108:13.
26. Liu, Y., Xu, W., Wang, J., Zhu, L., Guo, B., Chen, F., and Wang, G. 2011. General planar quadrilateral mesh design using conjugate direction field. ACM Trans. Graph. 30, 6, 140:1–140:10.
27. Mitchell, S. A. 2000. High fidelity interval assignment. Int. J. Comput. Geometry Appl. 10, 4, 399–415.
28. Myles, A., and Zorin, D. 2012. Global parametrization by incremental flattening. In Proc. SIGGRAPH 2012, 109:1–109:11.
29. Myles, A., and Zorin, D. 2013. Controlled-distortion constrained global parametrization. ACM Trans. Graph. 32, 4, 105:1–105:14.
30. Myles, A., Pietroni, N., Kovacs, D., and Zorin, D. 2010. Feature-aligned T-meshes. In Proc. SIGGRAPH 2010, 117:1–117:11.
31. Myles, A., Pietroni, N., and Zorin, D. 2014. Robust field-aligned global parametrization. In Proc. SIGGRAPH 2014, 135:1–135:14.
32. Nožička, F., Guddat, J., Hollatz, H., and Bank, B. 1974. Theorie der linearen Parametrischen Optimierung. Akademie-Verlag, Berlin.
33. Panozzo, D., Puppo, E., Tarini, M., and Sorkine-Hornung, O. 2014. Frame fields: Anisotropic and non-orthogonal cross fields. ACM Trans. Graph. 33, 4.
34. Pietroni, N., Tarini, M., and Cignoni, P. 2010. Almost isometric mesh parameterization through abstract domains. IEEE Trans. Vis. Comput. Graph. 16, 4, 621–635.
35. Pietroni, N., Tarini, M., Sorkine, O., and Zorin, D. 2011. Global parametrization of range image sets. ACM Trans. Graph. 30, 6, 149:1–149:10.
36. Pietroni, N., Tonelli, D., Puppo, E., Froli, M., Scopigno, R., and Cignoni, P. 2015. Statics aware grid shells. Computer Graphics Forum 34, 2, 627–641.
37. Purnomo, B., Cohen, J. D., and Kumar, S. 2004. Seamless texture atlases. In Proc. Symp. Geom. Proc., 65–74.
38. Ray, N., Li, W. C., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Trans. Graph. 25, 1460–1485.
39. Ray, N., Nivoliers, V., Lefebvre, S., and Lévy, B. 2010. Invisible seams. Comput. Graph. Forum 29, 4, 1489–1496.
40. Rockafellar, R. T. 1970. Convex analysis. Princeton Mathematical Series. Princeton University Press, Princeton, N. J.
41. Schilling, C. H., Letscher, D., and Palsson, B. O. 2000. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 203, 3, 229–248.
42. Sorkine, O., Cohen-Or, D., Goldenthal, R., and Lischinski, D. 2002. Bounded-distortion piecewise mesh parameterization. In IEEE Visualization, 355–362.
43. Tam, T. K. H., and Armstrong, C. G. 1993. Finite element mesh control by integer programming. International Journal for Numerical Methods in Engineering 36, 15, 2581–2605.
44. Tarini, M., Puppo, E., Panozzo, D., Pietroni, N., and Cignoni, P. 2011. Simple quad domains for field aligned mesh parametrization. Proc. SIGGRAPH Asia 2011, 142:1–142:12.
45. Tomás, A. P., and Filgueiras, M. 1997. An algorithm for solving systems of linear diophantine equations in naturals. In Progress in Artificial Intelligence, vol. 1323 of Lecture Notes in Computer Science. 73–84.
46. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. In Proc. SGP ’06, 201–210.
47. Tutte, W. T. 1963. How to draw a graph. Proc Lond Math Soc 13, 743–767.
48. Weber, O., and Zorin, D. 2014. Locally injective parametrization with arbitrary fixed boundaries. ACM Trans. Graph. 33, 4, 75:1–75:12.
49. Zhang, Y., Bajaj, C., and Xu, G. 2009. Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. Comm. Num. Meth. in Eng. 25, 1, 1–18.
50. Zhang, M., Huang, J., Liu, X., and Bao, H. 2010. A wave-based anisotropic quadrangulation method. In Proc. SIGGRAPH 2010, 118:1–118:8.