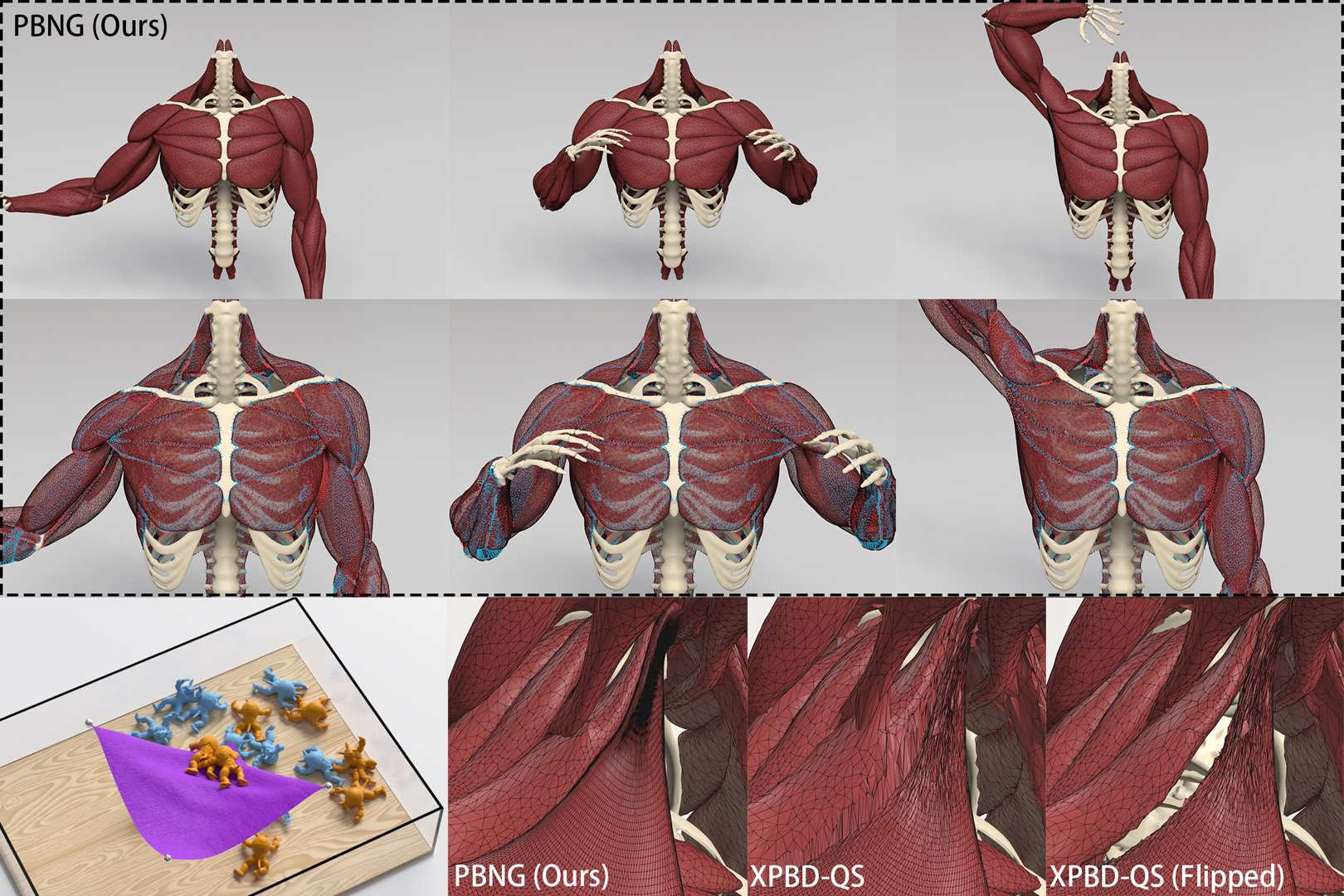
“Position-based Nonlinear Gauss-Seidel for Quasistatic Hyperelasticity”
Conference:
Type(s):
Title:
- Position-based Nonlinear Gauss-Seidel for Quasistatic Hyperelasticity
Presenter(s)/Author(s):
Abstract:
We show that a position-based, rather than constraint-based, nonlinear Gauss-Seidel approach resolves a number of issues with PBD, particularly in the quasistatic setting. Our approach retains the essential PBD feature of stable behavior with constrained computational budgets but also allows for convergent behavior with expanded budgets.
References:
[1]
Anonymous. 2023. Supplementary Technical Document (2023).
[2]
R. Atkin and R. Craine. 1976. Continuum theories of mixtures: basic theory and historical development. Quart J Mech App Math 29, 2 (1976), 209–244.
[3]
S. Bailey, D. Otte, P. Dilorenzo, and J. O’Brien. 2018. Fast and Deep Deformation Approximations. ACM Trans Graph 37, 4 (Aug. 2018), 119:1–12.
[4]
D. Baraff and A. Witkin. 1998. Large Steps in Cloth Simulation. In Proc ACM SIGGRAPH (SIGGRAPH ’98). 43–54.
[5]
H. Bertiche, M. Madadi, and S. Escalera. 2021. PBNS: Physically Based Neural Simulator for Unsupervised Garment Pose Space Deformation. arXiv:2012.11310 [cs.CV]
[6]
D. Bertsekas. 1997. Nonlinear programming. J Op Res Soc 48, 3 (1997), 334–334.
[7]
J. Bonet and R. Wood. 2008. Nonlinear continuum mechanics for finite element analysis. Cambridge University Press.
[8]
S. Bouaziz, S. Martin, T. Liu, L. Kavan, and M. Pauly. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. ACM Trans Graph 33, 4 (2014), 154:1–154:11.
[9]
S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning 3, 1 (2011), 1–122.
[10]
A. Brandt. 1977. Multi-level adaptive solutions to boundary-value problems. Math Comp 31, 138 (1977), 333–390.
[11]
I. Chao, U. Pinkall, P. Sanan, and P. Schr?der. 2010. A Simple Geometric Model for Elastic Deformations. ACM Trans Graph 29, 4, Article 38 (2010), 6 pages.
[12]
Y. Chen, Y. Han, J. Chen, MS. a, R. Fedkiw, and J. Teran. 2023. Primal Extended Position Based Dynamics for Hyperelasticity. In Proceedings of the 16th ACM SIGGRAPH Conference on Motion, Interaction and Games (MIG ’23). Article 21, 10 pages.
[13]
N. Chentanez, M. Macklin, M. M?ller, S. Jeschke, and T. Kim. 2020. Cloth and Skin Deformation with a Triangle Mesh Based Convolutional Neural Network. Comp Graph Forum 39, 8 (2020), 123–134.
[14]
O. Etzmuss, J. Gross, and W. Strasser. 2003. Deriving a particle system from continuum mechanics for the animation of deformable objects. IEEE Trans Vis Comp Graph 9, 4 (Oct. 2003), 538–550.
[15]
M. Fratarcangeli, T. Valentina, and F. Pellacini. 2016. Vivace: a practical gauss-seidel method for stable soft body dynamics. ACM Trans Graph 35, 6 (Nov 2016), 1–9.
[16]
T. Gast, C. Fu, C. Jiang, and J. Teran. 2016. Implicit-shifted Symmetric QR Singular Value Decomposition of 3×3 Matrices. Technical Report. University of California Los Angeles.
[17]
T. Gast, C. Schroeder, A. Stomakhin, C. Jiang, and J. Teran. 2015. Optimization Integrator for Large Time Steps. IEEE Trans Vis Comp Graph 21, 10 (2015), 1103–1115.
[18]
Z. Geng, D. Johnson, and R. Fedkiw. 2020. Coercing machine learning to output physically accurate results. J Comp Phys 406 (2020), 109099.
[19]
O. Gonzalez and A. Stuart. 2008. A first course in continuum mechanics. Cambridge University Press.
[20]
F. Hecht, Y. Lee, J. Shewchuk, and J. O’Brien. 2012. Updated Sparse Cholesky Factors for Corotational Elastodynamics. ACM Trans Graph 31, 5, Article 123 (2012), 13 pages.
[21]
N. Jin, Y. Zhu, Z. Geng, and R. Fedkiw. 2020. A Pixel-Based Framework for Data-Driven Clothing. In Proc ACM SIGGRAPH/Eurographics Symp Comp Anim (Virtual Event, Canada) (SCA ’20). Eurographics Association, Article 13, 10 pages.
[22]
Y. Jin, Y. Han, Z. Geng, J. Teran, and R. Fedkiw. 2022. Analytically Integratable Zero-Restlength Springs for Capturing Dynamic Modes Unrepresented by Quasistatic Neural Networks. In ACM SIGGRAPH 2022 Conf Proc (Vancouver, BC, Canada) (SIGGRAPH ’22). ACM, New York, NY, USA, Article 37, 9 pages.
[23]
S. Kovalsky, M. Galun, and Y. Lipman. 2016. Accelerated Quadratic Proxy for Geometric Optimization. ACM Trans Graph 35, 4, Article 134 (2016), 11 pages.
[24]
L. Lan, M. Li, C. Jiang, H. Wang, and Y. Yang. 2023. Second-order Stencil Descent for Interior-point Hyperelasticity. ACM Trans Graph 42, 4 (2023), 108:1–108:16.
[25]
M. Li, M. Gao, T. Langlois, C. Jiang, and D. Kaufman. 2019. Decomposed Optimization Time Integrator for Large-Step Elastodynamics. ACM Trans Graph 38, 4 (jul 2019), 10 pages.
[26]
L. Liu, L. Zhang, Y. Xu, C. Gotsman, and S. Gortler. 2008. A Local/Global Approach to Mesh Parameterization. In Proc Symp Geom Proc (SGP ’08). Eurograph Assoc, 1495?1504.
[27]
T. Liu, A. Bargteil, J. O’Brien, and L. Kavan. 2013. Fast Simulation of Mass-Spring Systems. ACM Trans Graph 32, 6 (2013), 209:1–7.
[28]
T. Liu, S. Bouaziz, and L. Kavan. 2017. Quasi-Newton Methods for Real-Time Simulation of Hyperelastic Materials. ACM Trans Graph 36, 4, Article 116a (2017), 16 pages.
[29]
R. Luo, T. Shao, H. Wang, W. Xu, X. Chen, K. Zhou, and Y. Yang. 2020. NNWarp: Neural Network-Based Nonlinear Deformation., 1745–1759 pages.
[30]
M. Macklin and M. Muller. 2021. A Constraint-based Formulation of Stable Neo-Hookean Materials. In Motion, Interaction and Games. ACM, 1–7.
[31]
M. Macklin, M. M?ller, and N. Chentanez. 2016. XPBD: Position-Based Simulation of Compliant Constrained Dynamics. In Proc 9th Int Conf Motion Games (Burlingame, California) (MIG ’16). ACM, 49?54.
[32]
S. Martin, B. Thomaszewski, E. Grinspun, and M. Gross. 2011. Example-Based Elastic Materials. In ACM SIGGRAPH 2011 (Vancouver, British Columbia, Canada) (SIGGRAPH ’11). ACM, Article 72, 8 pages.
[33]
A. McAdams, Y. Zhu, A. Selle, M. Empey, R. Tamstorf, J. Teran, and E. Sifakis. 2011. Efficient Elasticity for Character Skinning with Contact and Collisions. ACM Trans Graph 30, 4 (2011), 37:1–37:12.
[34]
M. Tournier, M. Nesme, B. Gilles, and F. Faure. 2015. Stable Constrained Dynamics. ACM Trans Graph (2015), 1–10.
[35]
M. M?ller, J. Dorsey, L. McMillan, R. Jagnow, and B. Cutler. 2002. Stable real-time deformations. In Proc 2002 ACM SIGGRAPH/Eurograph Symp Comp Anim. 49–54.
[36]
M. M?ller and M. Gross. 2004. Interactive virtual materials. In Proc Graph Int. Canadian Human-Computer Communications Society, 239–246.
[37]
M. M?ller, B. Heidelberger, M. Hennix, and J. Ratcliff. 2007. Position based dynamics. J Vis Comm Im Rep 18, 2 (2007), 109–118.
[38]
R. Narain, M. Overby, and G. Brown. 2016. ADMM Projective Dynamics: Fast Simulation of General Constitutive Models. In Proc ACM SIGGRAPH/Eurograph Symp Comp Anim (Zurich, Switzerland) (SCA ’16). Eurograph Assoc, 21?28.
[39]
J. Neuberger. 1985. Steepest descent and differential equations. J Math Soc Japan 37, 2 (1985), 187–195.
[40]
J. Nocedal and S. Wright. 2006. Conjugate gradient methods. Num Opt (2006), 101–134.
[41]
M. Rabinovich, R. Poranne, D. Panozzo, and O. Sorkine-Hornung. 2017. Scalable Locally Injective Mappings. ACM Trans Graph 36, 2, Article 16 (2017), 16 pages.
[42]
R. Schmedding and M. Teschner. 2008. Inversion handling for stable deformable modeling. Vis Comp 24, 7–9 (2008), 625–633.
[43]
E. Sifakis and J. Barbic. 2012. FEM simulation of 3D deformable solids: a practitioner’s guide to theory, discretization and model reduction. In ACM SIGGRAPH 2012 Courses (SIGGRAPH ’12). ACM, 20:1–20:50.
[44]
B. Smith, F. Goes, and T. Kim. 2019. Analytic eigensystems for isotropic distortion energies. ACM Trans Graph (TOG) 38, 1 (2019), 1–15.
[45]
B. Smith, F. De Goes, and T. Kim. 2018. Stable neo-hookean flesh simulation. ACM Trans Grap (TOG) 37, 2 (2018), 1–15.
[46]
O. Sorkine and M. Alexa. 2007. As-Rigid-As-Possible Surface Modeling. In EUROGRAPHICS SYMPOSIUM ON GEOMETRY PROCESSING.
[47]
A. Stern and M. Desbrun. 2006. Discrete Geometric Mechanics for Variational Time Integrators. In ACM SIGGRAPH 2006 Courses (Boston, Massachusetts) (SIGGRAPH ’06). ACM, 75?80.
[48]
A. Stomakhin, R. Howes, C. Schroeder, and J. Teran. 2012. Energetically consistent invertible elasticity. In Proc Symp Comp Anim. 25–32.
[49]
J. Teran, E. Sifakis, G. Irving, and R. Fedkiw. 2005. Robust quasistatic finite elements and flesh simulation. In Proc 2005 ACM SIGGRAPH/Eurograph Symp Comp Anim. 181–190.
[50]
H. Wang. 2015. A Chebyshev Semi-Iterative Approach for Accelerating Projective and Position-Based Dynamics. ACM Trans Graph 34, 6, Article 246 (nov 2015), 9 pages.
[51]
H. Wang and Y. Yang. 2016. Descent methods for elastic body simulation on the GPU. ACM Trans Graph 35, 6 (Nov 2016), 1–10.
[52]
Z. Wang, L. Wu, M. Fraftarcangeli, M. Tang, and H. Wang. 2018. Parallel Multigrid
[53]
for nonlinear cloth simulation. Computer Graphics Forum 37, 7 (2018), 131–141.
[54]
B. Witemeyer, N. Weidner, T. Davis, T. Kim, and S. Sueda. 2021. QLB: Collision-Aware Quasi-Newton Solver with Cholesky and L-BFGS for Nonlinear Time Integration. In Proc 14th ACM SIGGRAPH Conf Mot Int Games (MIG ’21). ACM, Article 14, 7 pages.
[55]
Y. Zhu, R. Bridson, and D. Kaufman. 2018. Blended Cured Quasi-Newton for Distortion Optimization. ACM Trans Graph 37, 4, Article 40 (jul 2018), 14 pages.