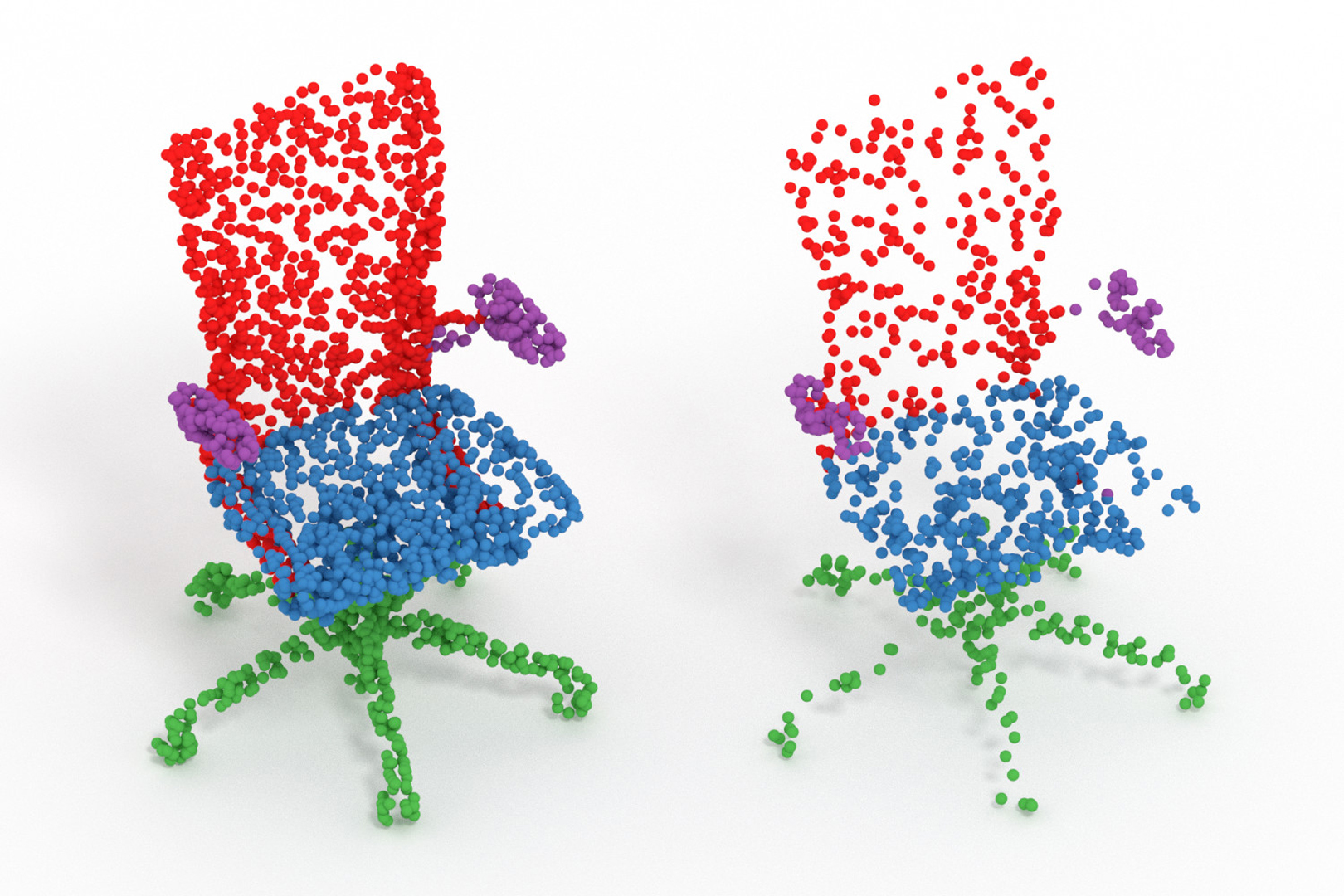
“Monte Carlo convolution for learning on non-uniformly sampled point clouds”
Conference:
Type(s):
Title:
- Monte Carlo convolution for learning on non-uniformly sampled point clouds
Session/Category Title:
- Learning geometry
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Deep learning systems extensively use convolution operations to process input data. Though convolution is clearly defined for structured data such as 2D images or 3D volumes, this is not true for other data types such as sparse point clouds. Previous techniques have developed approximations to convolutions for restricted conditions. Unfortunately, their applicability is limited and cannot be used for general point clouds. We propose an efficient and effective method to learn convolutions for non-uniformly sampled point clouds, as they are obtained with modern acquisition techniques. Learning is enabled by four key novelties: first, representing the convolution kernel itself as a multilayer perceptron; second, phrasing convolution as a Monte Carlo integration problem, third, using this notion to combine information from multiple samplings at different levels; and fourth using Poisson disk sampling as a scalable means of hierarchical point cloud learning. The key idea across all these contributions is to guarantee adequate consideration of the underlying non-uniform sample distribution function from a Monte Carlo perspective. To make the proposed concepts applicable to real-world tasks, we furthermore propose an efficient implementation which significantly reduces the GPU memory required during the training process. By employing our method in hierarchical network architectures we can outperform most of the state-of-the-art networks on established point cloud segmentation, classification and normal estimation benchmarks. Furthermore, in contrast to most existing approaches, we also demonstrate the robustness of our method with respect to sampling variations, even when training with uniformly sampled data only. To support the direct application of these concepts, we provide a ready-to-use TensorFlow implementation of these layers at https://github.com/viscom-ulm/MCCNN.
References:
1. Andrew Adams, Jongmin Baek, and Myers Abraham Davis. 2010. Fast High-Dimensional Filtering Using the Permutohedral Lattice. Comp. Graph. Forum (Proc. Eurographics) 29, 2 (2010), 753–62.Google ScholarCross Ref
2. Matan Atzmon, Haggai Maron, and Yaron Lipman. 2018. Point Convolutional Neural Networks by Extension Operators. ACM Trans. Graph. (Proc. SIGGRAPH) 37, 3 (2018). Google ScholarDigital Library
3. Robert L. Cook. 1986. Stochastic Sampling in Computer Graphics. ACM Trans. Graph. 5, 1 (1986), 51–72. Google ScholarDigital Library
4. Angela Dai, Angel X. Chang, Manolis Savva, Maciej Halber, Thomas Funkhouser, and Matthias Nießner. 2017. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. In CVPR.Google Scholar
5. Angela Dai and Matthias Nießner. 2018. 3DMV: Joint 3D-Multi-View Prediction for 3D Semantic Scene Segmentation. (2018). arXiv:1803.10409Google Scholar
6. Yuval Eldar, Michael Lindenbaum, Moshe Porat, and Yehoshua Y Zeevi. 1997. The farthest point strategy for progressive image sampling. IEEE Trans. Image Proc. 6, 9 (1997), 1305–15. Google ScholarDigital Library
7. Simon Green. 2008. Cuda particles. NVIDIA whitepaper (2008).Google Scholar
8. Fabian Groh, Patrick Wieschollek, and Hendrik P. A. Lensch. 2018. Flex-Convolution (Deep Learning Beyond Grid-Worlds). (2018). arXiv:1803.07289Google Scholar
9. Paul Guerrero, Yanir Kleiman, Maks Ovsjanikov, and Niloy J. Mitra. 2018. PCPNet: Learning Local Shape Properties from Raw Point Clouds. Comp. Graph. Forum (Proc. Eurographics) (2018).Google Scholar
10. T. Hales, M. Adams, G. Bauer, T. D. Dang, J. Harrison, L. T. Hoang, C. Kaliszyk, V. Magron, S. McLaughlin, T. Nguyen, and et al. 2017. A formal proof of the Keppler conjecture. Forum Math., Pi 5 (2017).Google Scholar
11. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Deep Residual Learning for Image Recognition. (2015). arXiv:1512.03385Google Scholar
12. Gao Huang, Zhuang Liu, and Kilian Q. Weinberger. 2016. Densely Connected Convolutional Networks. (2016). arXiv:1608.06993Google Scholar
13. H Kahn and A Marshall. 1953. Methods of Reducing Sample Size in Monte Carlo Computations. 1 (1953), 263–78.Google ScholarCross Ref
14. Malvin H. Kalos and Paula A. Whitlock. 1986. Monte Carlo Methods. Wiley-Interscience, New York, NY, USA. Google ScholarDigital Library
15. Roman Klokov and Victor Lempitsky. 2017. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In ICCV. 863–72.Google Scholar
16. Yangyan Li, Rui Bu, Mingchao Sun, and Baoquan Chen. 2018. PointCNN. (2018). arXiv:1801.07791Google Scholar
17. Harald Niederreiter. 1992. Random Number Generation and quasi-Monte Carlo Methods. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA. Google Scholar
18. Emanuel Parzen. 1962. On Estimation of a Probability Density Function and Mode. Ann. Math. Statist. 33, 3 (09 1962), 1065–76.Google Scholar
19. Charles R Qi, Hao Su, Kaichun Mo, and Leonidas J Guibas. 2017a. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. CVPR (2017).Google Scholar
20. Charles R Qi, Li Yi, Hao Su, and Leonidas J Guibas. 2017b. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. CoPP (2017).Google Scholar
21. Olaf Ronneberger, Philipp Fischer, and Thomas Brox. 2015. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proc. MICCAI. 234–41.Google ScholarCross Ref
22. Murray Rosenblatt. 1956. Remarks on Some Nonparametric Estimates of a Density Function. Ann. Math. Statist. 27, 3 (09 1956), 832–7.Google Scholar
23. David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. 1986. Learning representations by back-propagating errors. Nature 323, 6088 (1986), 533.Google ScholarCross Ref
24. Yiru Shen, Chen Feng, Yaoqing Yang, and Dong Tian. 2017. Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling. (2017). arXiv:1712.06760Google Scholar
25. Hang Su, Varun Jampani, Deqing Sun, Subhransu Maji, Evangelos Kalogerakis, Ming-Hsuan Yang, and Jan Kautz. 2018. SPLATNet: Sparse Lattice Networks for Point Cloud Processing. CVPR (2018).Google Scholar
26. Matthias Teschner, Bruno Heidelberger, Matthias Müller, Danat Pomerantes, and Markus H Gross. 2003. Optimized Spatial Hashing for Collision Detection of Deformable Objects.. In VMV, Vol. 3. 47–54.Google Scholar
27. Peng-Shuai Wang, Yang Liu, Yu-Xiao Guo, Chun-Yu Sun, and Xin Tong. 2017. O-CNN: Octree-based Convolutional Neural Networks for 3D Shape Analysis. ACM Trans. Graph. 36, 4 (2017), 72:1–72:11. Google ScholarDigital Library
28. Yue Wang, Yongbin Sun, Ziwei Liu, Sanjay E. Sarma, Michael M. Bronstein, and Justin M. Solomon. 2018. Dynamic Graph CNN for Learning on Point Clouds. (2018). arXiv:1801.07829Google Scholar
29. Li-Yi Wei. 2008. Parallel Poisson Disk Sampling. ACM Trans. Graph. 27, 3 (2008), 20:1–20:9. Google ScholarDigital Library
30. Zhirong Wu, S. Song, A. Khosla, Fisher Yu, Linguang Zhang, Xiaoou Tang, and J. Xiao. 2015. 3D ShapeNets: A deep representation for volumetric shapes. In CVPR. 1912–1920.Google Scholar
31. Yifan Xu, Tianqi Fan, Mingye Xu, Long Zeng, and Yu Qiao. 2018. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters. (2018). arXiv:1803.11527Google Scholar
32. Li Yi, Vladimir G. Kim, Duygu Ceylan, I-Chao Shen, Mengyan Yan, Hao Su, Cewu Lu, Qixing Huang, Alla Sheffer, and Leonidas Guibas. 2016. A Scalable Active Framework for Region Annotation in 3D Shape Collections. ACM Trans. Graph. (Proc. SIGGRAPH Asia) (2016). Google ScholarDigital Library