“Modeling curved folding with freeform deformations” by Rabinovich, Hoffmann and Sorkine-Hornung
Conference:
Type(s):
Title:
- Modeling curved folding with freeform deformations
Session/Category Title:
- Network
Presenter(s)/Author(s):
Moderator(s):
Abstract:
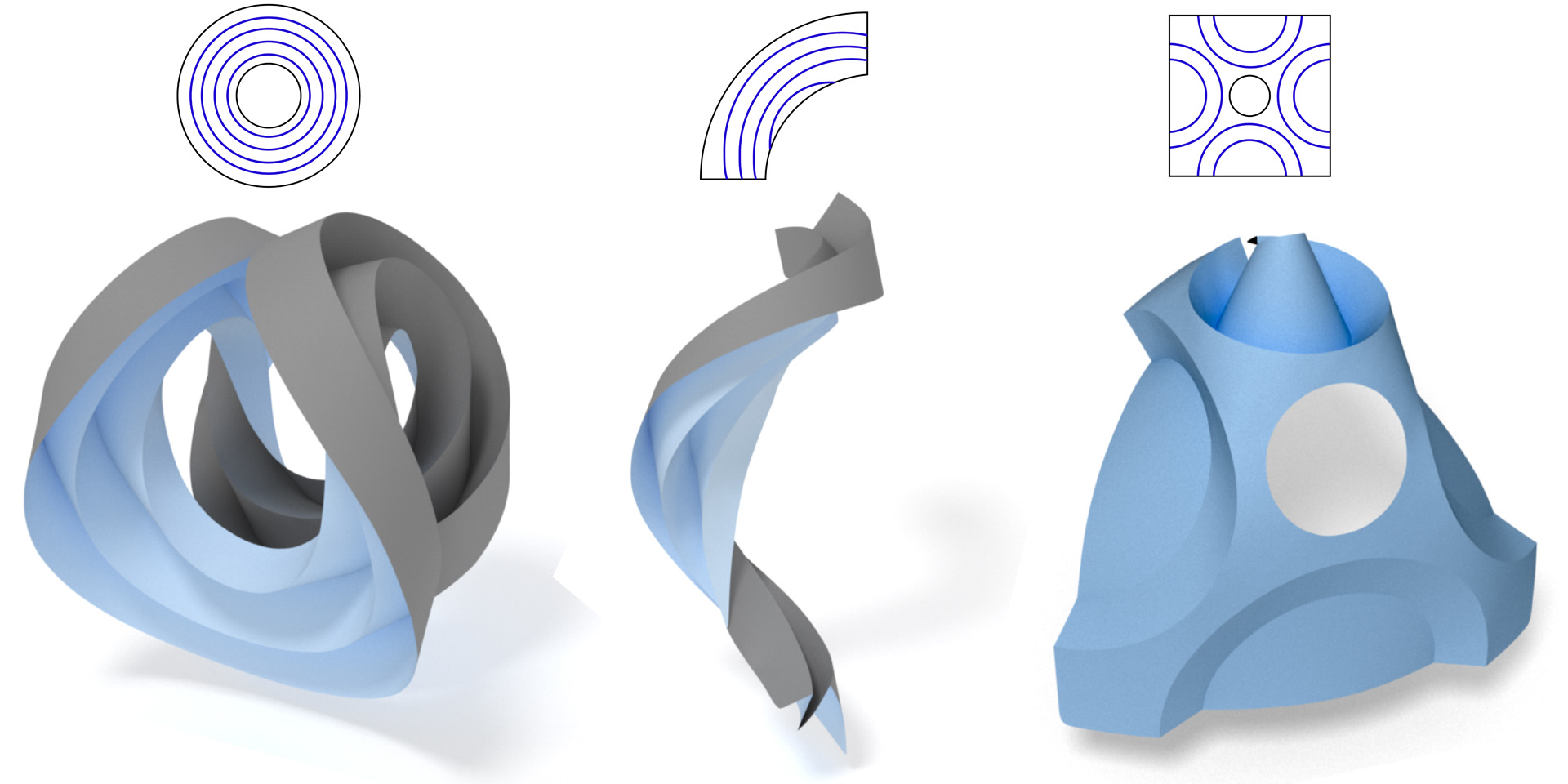
We present a computational framework for interactive design and exploration of curved folded surfaces. In current practice, such surfaces are typically created manually using physical paper, and hence our objective is to lay the foundations for the digitalization of curved folded surface design. Our main contribution is a discrete binary characterization for folds between discrete developable surfaces, accompanied by an algorithm to simultaneously fold creases and smoothly bend planar sheets. We complement our algorithm with essential building blocks for curved folding deformations: objectives to control dihedral angles and mountain-valley assignments. We apply our machinery to build the first interactive freeform editing tool capable of modeling bending and folding of complicated crease patterns.
References:
1. E. D. Adler. 2004. ” A New Unity!” The Art and Pedagogy of Josef Albers. Ph.D. Dissertation.Google Scholar
2. Q. Alessio. 2012. Membrane locking in discrete shell theories. Ph.D. Dissertation. Niedersächsische Staats-und Universitätsbibliothek Göttingen.Google Scholar
3. M. Bergou, M. Wardetzky, D. Harmon, D. Zorin, and E. Grinspun. 2006. A quadratic bending model for inextensible surfaces. In Symposium on Geometry Processing. 227–230.Google Scholar
4. P. Bo, Y. Zheng, X. Jia, and C. Zhang. 2019. Multi-strip smooth developable surfaces from sparse design curves. Computer-Aided Design 114 (2019).Google Scholar
5. M. Botsch, M. Pauly, M. H. Gross, and L. Kobbelt. 2006. PriMo: coupled prisms for intuitive surface modeling. In Symposium on Geometry Processing. 11–20.Google Scholar
6. R. Burgoon, Z. J. Wood, and E. Grinspun. 2006. Discrete Shells Origami. In Computers and Their Applications.Google Scholar
7. H. U. Buri, I. Stotz, and Y. Weinand. 2011. Curved Folded Plate Timber Structures. In IABSE-IASS 2011 London Symposium. IABSE-IASS.Google Scholar
8. D. Chapelle and K.-J. Bathe. 1998. Fundamental considerations for the finite element analysis of shell structures. Computers & Structures 66, 1 (1998), 19–36.Google ScholarCross Ref
9. A. De Coninck, B. De Baets, D. Kourounis, F. Verbosio, O. Schenk, S. Maenhout, and J. Fostier. 2016. Needles: Toward Large-Scale Genomic Prediction with Marker-by-Environment Interaction. Genetics 203, 1 (2016), 543–555. arXiv:http://www.genetics.org/content/203/1/543.full.pdf Google ScholarCross Ref
10. E. D. Demaine, M. L. Demaine, V. Hart, G. N. Price, and T. Tachi. 2011b. (Non) existence of pleated folds: how paper folds between creases. Graphs and Combinatorics 27, 3 (2011), 377–397.Google ScholarDigital Library
11. E. D. Demaine, M. L. Demaine, D. A. Hufman, D. Koschitz, and T. Tachi. 2015. Characterization of curved creases and rulings: Design and analysis of lens tessellations. Origami 6 (2015), 209–230.Google ScholarCross Ref
12. E. D. Demaine, M. L. Demaine, D. A. Hufman, D. Koschitz, and T. Tachi. 2018. Conic Crease Patterns with Reflecting Rule Lines. arXiv preprint arXiv:1812.01167. (2018).Google Scholar
13. E. D. Demaine, M. L. Demaine, and D. Koschitz. 2011a. Reconstructing David Hufman’s legacy in curved-crease folding. Origami 5 (2011), 39–52.Google ScholarCross Ref
14. E. D. Demaine, M. L. Demaine, D. Koschitz, and T. Tachi. 2011c. Curved crease folding: a review on art, design and mathematics. In Proceedings of the IABSE-IASS Symposium: Taller, Longer, Lighter. 20–23.Google Scholar
15. E. D. Demaine and J. O’Rourke. 2007. Geometric Folding Algorithms: Linkages, Origami, Polyhedra. Cambridge University Press.Google ScholarDigital Library
16. M. P. do Carmo. 1976. Differential Geometry of Curves and Surfaces. Prentice-Hall.Google Scholar
17. J. P. Duncan and J. Duncan. 1982. Folded developables. Proc. R. Soc. Lond. A 383, 1784 (1982), 191–205.Google Scholar
18. W. H. Frey. 2002. Boundary triangulations approximating developable surfaces that interpolate a closed space curve. International Journal of Foundations of Computer Science 13, 02 (2002), 285–302.Google ScholarCross Ref
19. W. H. Frey. 2004. Modeling buckled developable surfaces by triangulation. Computer Aided Design 36, 4 (2004), 299–313.Google ScholarCross Ref
20. S. Fröhlich and M. Botsch. 2011. Example-Driven Deformations Based on Discrete Shells. Comput. Graph. Forum 30, 8 (2011), 2246–2257.Google ScholarCross Ref
21. D. Fuchs and S. Tabachnikov. 1999. More on paperfolding. The American Mathematical Monthly 106, 1 (1999), 27–35.Google ScholarCross Ref
22. D. Fuchs and S. Tabachnikov. 2007. Mathematical omnibus: thirty lectures on classic mathematics. Springer.Google Scholar
23. R. Goldenthal, D. Harmon, R. Fattal, M. Bercovier, and E. Grinspun. 2007. Efficient simulation of inextensible cloth. ACM Trans. Graph. 26, 3 (2007), 49.Google ScholarDigital Library
24. F. Gramazio and M. Kohler. 2014. Made by robots: challenging architecture at a larger scale. John Wiley & Sons.Google Scholar
25. E. Grinspun, A. N. Hirani, M. Desbrun, and P. Schröder. 2003. Discrete Shells. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation. 62–67. http://dl.acm.org/citation.cfm?id=846276.846284Google Scholar
26. B. Grünbaum. 1972. Arrangements and spreads. American Mathematical Society.Google Scholar
27. D. A. Hufman. 1976. Curvature and creases: a primer on paper. IEEE Trans. Computers 25, 10 (1976), 1010–1019.Google ScholarDigital Library
28. M. Kilian, S. Flöry, Z. Chen, N. J. Mitra, A. Sheffer, and H. Pottmann. 2008. Curved folding. ACM Trans. Graph. 27, 3 (2008), 75:1–75:9.Google ScholarDigital Library
29. M. Kilian, A. Monszpart, and N. J. Mitra. 2017. String actuated curved folded surfaces. ACM Trans. Graph. 36, 3 (2017), 25:1–25:13.Google ScholarDigital Library
30. D. Kourounis, A. Fuchs, and O. Schenk. 2018. Towards the Next Generation of Multiperiod Optimal Power Flow Solvers. IEEE Transactions on Power Systems PP, 99 (2018), 1–10. Google ScholarCross Ref
31. Z. Li, S. Wang, and X. Lin. 2012. Variable selection and estimation in generalized linear models with the seamless L0 penalty. Canadian Journal of Statistics 40, 4 (2012), 745–769.Google ScholarCross Ref
32. Y. Liu, H. Pottmann, J. Wallner, Y.-L. Yang, and W. Wang. 2006. Geometric modeling with conical meshes and developable surfaces. ACM Trans. Graph. 25, 3 (2006).Google ScholarDigital Library
33. J. Mitani. 2009. A design method for 3D origami based on rotational sweep. Computer-Aided Design and Applications 6, 1 (2009), 69–79.Google ScholarCross Ref
34. J. Mitani. 2012. Column-shaped origami design based on mirror reflections. Journal for Geometry and Graphics 16, 2 (2012), 185–194.Google Scholar
35. J. Mitani. 2019. Curved-Folding Origami Design. CRC Press.Google Scholar
36. J. Mitani and T. Igarashi. 2011. Interactive design of planar curved folding by reflection. In Proc. Pacific Graphics, Short Papers.Google Scholar
37. K. Mundilova. 2019. On mathematical folding of curved crease origami: Sliding developables and parametrizations of folds into cylinders and cones. Computer-Aided Design (2019). accepted for publication.Google Scholar
38. R. Narain, T. Pfaff, and J. F. O’Brien. 2013. Folding and Crumpling Adaptive Sheets. ACM Trans. Graph. 32, 4 (2013).Google ScholarDigital Library
39. R. Narain, A. Samii, and J. F. O’Brien. 2012. Adaptive anisotropic remeshing for cloth simulation. ACM transactions on graphics (TOG) 31, 6 (2012), 152.Google Scholar
40. J. Nocedal and S. J. Wright. 2006. Sequential quadratic programming. Springer.Google Scholar
41. R. Poranne, M. Tarini, S. Huber, D. Panozzo, and O. Sorkine-Hornung. 2017. Autocuts: Simultaneous Distortion and Cut Optimization for UV Mapping. ACM Transactions on Graphics (proceedings of ACM SIGGRAPH ASIA) 36, 6 (2017).Google ScholarDigital Library
42. H. Pottmann, M. Eigensatz, A. Vaxman, and J. Wallner. 2015. Architectural geometry. Computers & graphics 47 (2015), 145–164.Google Scholar
43. H. Pottmann and J. Wallner. 1999. Approximation algorithms for developable surfaces. Comput. Aided Geom. Des. 16, 6 (1999), 539 — 556. Google ScholarCross Ref
44. H. Pottmann and J. Wallner. 2001. Computational line geometry. Springer, Berlin, Heidelberg, New York.Google Scholar
45. M. Rabinovich, T. Hoffmann, and O. Sorkine-Hornung. 2018a. Discrete Geodesic Nets for Modeling Developable Surfaces. ACM Trans. Graph. 37, 2 (2018), 16.Google ScholarDigital Library
46. M. Rabinovich, T. Hoffmann, and O. Sorkine-Hornung. 2018b. The shape space of discrete orthogonal geodesic nets. In SIGGRAPH Asia 2018 Technical Papers. ACM, 228.Google Scholar
47. R. D. Resch. 1974. Portfolio of shaded computer images. Proc. IEEE 62, 4 (1974), 496–502.Google ScholarCross Ref
48. K. Rose, A. Sheffer, J. Wither, M.-P. Cani, and B. Thibert. 2007. Developable Surfaces from Arbitrary Sketched Boundaries. In Proc. Symposium on Geometry Processing. 163–172. http://dl.acm.org/citation.cfm?id=1281991.1282014Google Scholar
49. C. Schreck, D. Rohmer, and S. Hahmann. 2017. Interactive paper tearing. Computer Graphics Forum (Eurographics) 36, 2 (2017), 95–106.Google ScholarDigital Library
50. C. Schreck, D. Rohmer, S. Hahmann, M.-P. Cani, S. Jin, C. C. L. Wang, and J.-F. Bloch. 2015. Nonsmooth Developable Geometry for Interactively Animating Paper Crumpling. ACM Trans. Graph. 35, 1 (2015), 10. http://dblp.uni-trier.de/db/journals/tog/tog35.html#SchreckRHCJWB15Google ScholarDigital Library
51. J. Solomon, E. Vouga, M. Wardetzky, and E. Grinspun. 2012. Flexible developable surfaces. Comput. Graph. Forum 31, 5 (2012), 1567–1576.Google ScholarDigital Library
52. M. Spivak. 1999. A Comprehensive introduction to differential geometry, 1. Publish or Perish, Houston, TX. http://opac.inria.fr/record=b1117511Google Scholar
53. O. Stein, E. Grinspun, and K. Crane. 2018. Developability of triangle meshes. ACM Trans. Graph. 37, 4 (2018).Google ScholarDigital Library
54. T. Tachi. 2010. Freeform variations of origami. J. Geom. Graph 14, 2 (2010), 203–215.Google Scholar
55. T. Tachi. 2011. One-DOF rigid foldable structures from space curves. In Proceedings of the IABSE-IASS Symposium. 20–23.Google Scholar
56. T. Tachi. 2013. Composite rigid-foldable curved origami structure. In 1st International Conference on Transformable Architecture (Transformables 2013), Seville, Spain, Sept. 18–20.Google Scholar
57. C. Tang, P. Bo, J. Wallner, and H. Pottmann. 2016. Interactive design of developable surfaces. ACM Trans. Graph. 35, 2, Article 12 (2016), 12 pages.Google ScholarDigital Library
58. The CGAL Project. 2019. CGAL User and Reference Manual (4.14 ed.). CGAL Editorial Board. https://doc.cgal.org/4.14/Manual/packages.htmlGoogle Scholar
59. F. Verbosio, A. D. Coninck, D. Kourounis, and O. Schenk. 2017. Enhancing the scalability of selected inversion factorization algorithms in genomic prediction. Journal of Computational Science 22, Supplement C (2017), 99 — 108. Google ScholarCross Ref
60. R. Wein, E. Berberich, E. Fogel, D. Halperin, M. Hemmer, O. Salzman, and B. Zukerman. 2019. 2D Arrangements. In CGAL User and Reference Manual (4.14 ed.). CGAL Editorial Board. https://doc.cgal.org/4.14/Manual/packages.html#PkgArrangementOnSurface2Google Scholar
61. M. Wertheim. 2004. Cones, curves, shells, towers: He made paper jump to life. The New York Times 2, 4 (2004), 5.Google Scholar
62. B. Zukerman, R. Wein, and E. Fogel. 2019. 2D Intersection of Curves. In CGAL User and Reference Manual (4.14 ed.). CGAL Editorial Board. https://doc.cgal.org/4.14/Manual/packages.html#PkgSurfaceSweep2Google Scholar