“LiCROM: Linear-Subspace Continuous Reduced Order Modeling with Neural Fields” by Chang, Chen, Wang, Chiaramonte, Carlberg, et al. …
Conference:
Type(s):
Title:
- LiCROM: Linear-Subspace Continuous Reduced Order Modeling with Neural Fields
Session/Category Title:
- Deformable Solids
Presenter(s)/Author(s):
Abstract:
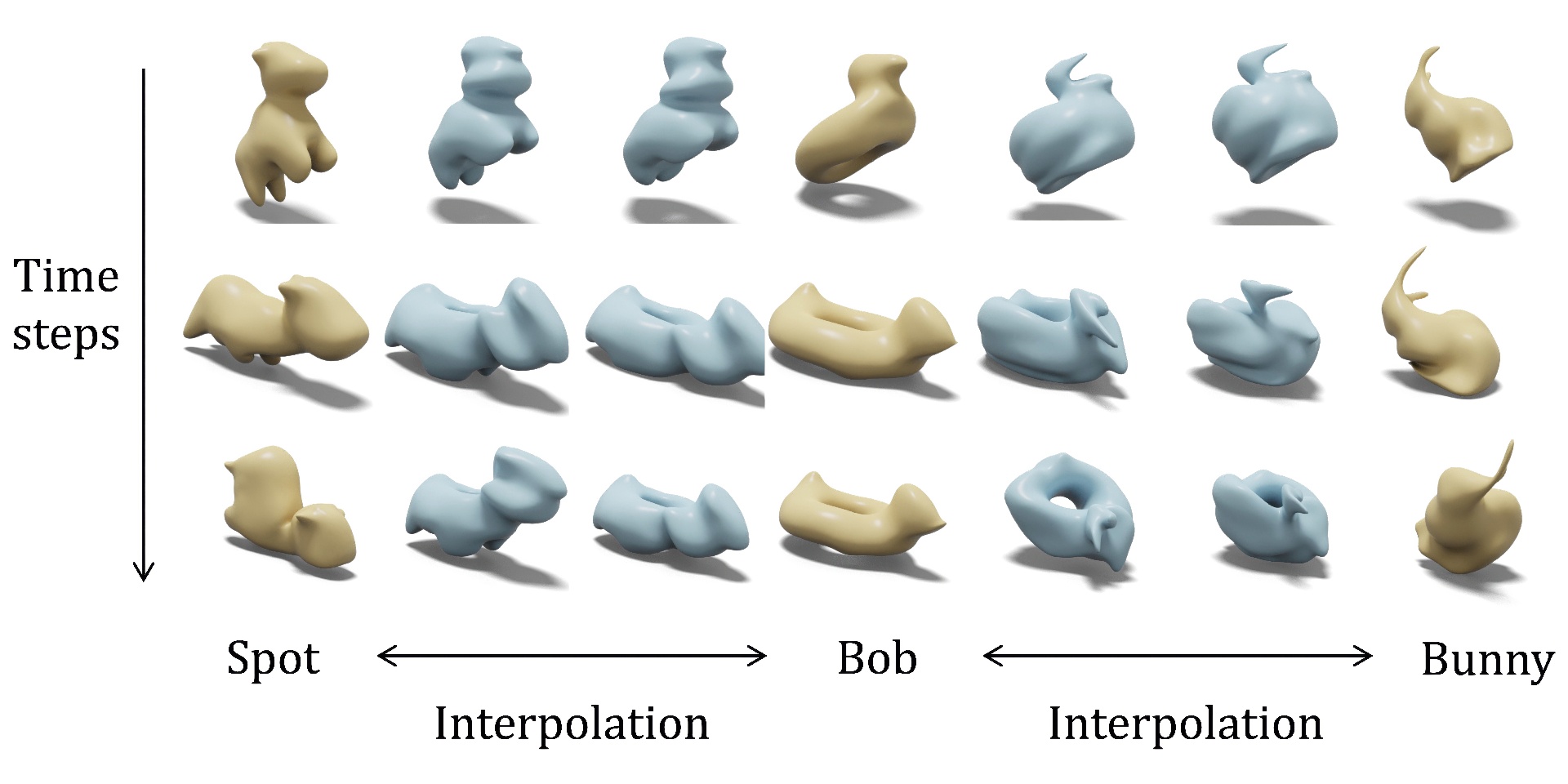
Linear reduced-order modeling (ROM) simplifies complex simulations by approximating the behavior of a system using a simplified kinematic representation. Typically, ROM is trained on input simulations created with a specific spatial discretization, and then serves to accelerate simulations with the same discretization. This discretization-dependence is restrictive. Becoming independent of a specific discretization would provide flexibility to mix and match mesh resolutions, connectivity, and type (tetrahedral, hexahedral) in training data; to accelerate simulations with novel discretizations unseen during training; and to accelerate adaptive simulations that temporally or parametrically change the discretization. We present a flexible, discretization-independent approach to reduced-order modeling. Like traditional ROM, we represent the configuration as a linear combination of displacement fields. Unlike traditional ROM, our displacement fields are continuous maps from every point on the reference domain to a corresponding displacement vector; these maps are represented as implicit neural fields. With linear continuous ROM (LiCROM), our training set can include multiple geometries undergoing multiple loading conditions, independent of their discretization. This opens the door to novel applications of reduced order modeling. For instance, we can accelerate simulations on geometries unseen during training, and simulations that modify the geometry at runtime, for instance via cutting, hole punching, and even swapping the entire mesh. Indeed, we achieve one-shot generalization by training on a single geometry but testing on multiple unseen geometries.
References:
[1]
Noam Aigerman, Kunal Gupta, Vladimir G. Kim, Siddhartha Chaudhuri, Jun Saito, and Thibault Groueix. 2022. Neural Jacobian Fields: Learning Intrinsic Mappings of Arbitrary Meshes. ACM Transactions on Graphics (TOG) 41, 4, Article 109 (jul 2022), 17 pages. https://doi.org/10.1145/3528223.3530141
[2]
Steven S An, Theodore Kim, and Doug L James. 2008a. Optimizing cubature for efficient integration of subspace deformations. ACM transactions on graphics (TOG) 27, 5 (2008), 1–10.
[3]
Steven S. An, Theodore Kim, and Doug L. James. 2008b. Optimizing Cubature for Efficient Integration of Subspace Deformations. ACM Transactions on Graphics (TOG) 27, 5, Article 165 (dec 2008), 10 pages. https://doi.org/10.1145/1409060.1409118
[4]
Jernej Barbič and Yili Zhao. 2011. Real-time large-deformation substructuring. ACM transactions on graphics (TOG) 30, 4 (2011), 1–8.
[5]
Jernej Barbič and Doug L. James. 2005. Real-Time Subspace Integration for St. Venant-Kirchhoff Deformable Models. ACM Transactions on Graphics (TOG) 24, 3 (jul 2005), 982–990. https://doi.org/10.1145/1073204.1073300
[6]
Otman Benchekroun, Jiayi Eris Zhang, Siddartha Chaudhuri, Eitan Grinspun, Yi Zhou, and Alec Jacobson. 2023. Fast Complementary Dynamics via Skinning Eigenmodes. ACM Transactions on Graphics (TOG) 42, 4, Article 106 (jul 2023), 21 pages. https://doi.org/10.1145/3592404
[7]
Peter Benner, Serkan Gugercin, and Karen Willcox. 2015. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM review 57, 4 (2015), 483–531.
[8]
Michel Bergmann, Laurent Cordier, and Jean-Pierre Brancher. 2005. Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Physics of fluids 17, 9 (2005), 097101.
[9]
Gal Berkooz, Philip Holmes, and John L Lumley. 1993. The proper orthogonal decomposition in the analysis of turbulent flows. Annual review of fluid mechanics 25, 1 (1993), 539–575.
[10]
Kevin Carlberg, Matthew Barone, and Harbir Antil. 2017. Galerkin v. least-squares Petrov–Galerkin projection in nonlinear model reduction. J. Comput. Phys. 330 (2017), 693–734.
[11]
Kevin Carlberg, Charbel Farhat, Julien Cortial, and David Amsallem. 2013. The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 242 (2013), 623–647.
[12]
Honglin Chen, Rundi Wu, Eitan Grinspun, Changxi Zheng, and Peter Yichen Chen. 2022. Implicit Neural Spatial Representations for Time-dependent PDEs. arXiv preprint arXiv:2210.00124 (2022).
[13]
Peter Yichen Chen, Maurizio M. Chiaramonte, Eitan Grinspun, and Kevin Carlberg. 2023a. Model reduction for the material point method via an implicit neural representation of the deformation map. J. Comput. Phys. 478 (2023), 111908. https://doi.org/10.1016/j.jcp.2023.111908
[14]
Peter Yichen Chen, Jinxu Xiang, Dong Heon Cho, Yue Chang, G A Pershing, Henrique Teles Maia, Maurizio M Chiaramonte, Kevin Thomas Carlberg, and Eitan Grinspun. 2023b. CROM: Continuous Reduced-Order Modeling of PDEs Using Implicit Neural Representations. In The Eleventh International Conference on Learning Representations. https://openreview.net/forum?id=FUORz1tG8Og
[15]
Yinbo Chen, Sifei Liu, and Xiaolong Wang. 2021. Learning Continuous Image Representation With Local Implicit Image Function. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 8628–8638.
[16]
Zhiqin Chen and Hao Zhang. 2019. Learning Implicit Fields for Generative Shape Modeling. In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 5932–5941. https://doi.org/10.1109/CVPR.2019.00609
[17]
Djork-Arné Clevert, Thomas Unterthiner, and Sepp Hochreiter. 2016. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arxiv:1511.07289 [cs.LG]
[18]
William Falcon and The PyTorch Lightning team. 2019. PyTorch Lightning. https://doi.org/10.5281/zenodo.3828935
[19]
Lawson Fulton, Vismay Modi, David Duvenaud, David I. W. Levin, and Alec Jacobson. 2019. Latent-space Dynamics for Reduced Deformable Simulation. Computer Graphics Forum (2019).
[20]
Kenneth C Hall, Jeffrey P Thomas, and Earl H Dowell. 2000. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows. AIAA journal 38, 10 (2000), 1853–1862.
[21]
Yuanming Hu, Tzu-Mao Li, Luke Anderson, Jonathan Ragan-Kelley, and Frédo Durand. 2019. Taichi: a language for high-performance computation on spatially sparse data structures. ACM Transactions on Graphics (TOG) 38, 6 (2019), 201.
[22]
Yixin Hu, Qingnan Zhou, Xifeng Gao, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2018. Tetrahedral Meshing in the Wild. ACM Transactions on Graphics (TOG) 37, 4, Article 60 (July 2018), 14 pages. https://doi.org/10.1145/3197517.3201353
[23]
Doug L James, Jernej Barbič, and Dinesh K Pai. 2006. Precomputed acoustic transfer: output-sensitive, accurate sound generation for geometrically complex vibration sources. ACM Transactions on Graphics (TOG) 25, 3 (2006), 987–995.
[24]
Robert K Katzschmann, Maxime Thieffry, Olivier Goury, Alexandre Kruszewski, Thierry-Marie Guerra, Christian Duriez, and Daniela Rus. 2019. Dynamically closed-loop controlled soft robotic arm using a reduced order finite element model with state observer. In 2019 2nd IEEE international conference on soft robotics (RoboSoft). IEEE, 717–724.
[25]
Byungsoo Kim, Vinicius C Azevedo, Nils Thuerey, Theodore Kim, Markus Gross, and Barbara Solenthaler. 2019. Deep fluids: A generative network for parameterized fluid simulations. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 59–70.
[26]
Theodore Kim and John Delaney. 2013. Subspace fluid re-simulation. ACM Transactions on Graphics (TOG) 32, 4 (2013), 1–9.
[27]
Theodore Kim and Doug L. James. 2009. Skipping Steps in Deformable Simulation with Online Model Reduction. ACM Transactions on Graphics (TOG) 28, 5 (dec 2009), 1–9. https://doi.org/10.1145/1618452.1618469
[28]
Diederik P. Kingma and Jimmy Ba. 2017. Adam: A Method for Stochastic Optimization. arxiv:1412.6980 [cs.LG]
[29]
Kookjin Lee and Kevin Carlberg. 2018. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. arXiv preprint arXiv:1812.08373 (2018).
[30]
Thuan Lieu, Charbel Farhat, and Michel Lesoinne. 2006. Reduced-order fluid/structure modeling of a complete aircraft configuration. Computer methods in applied mechanics and engineering 195, 41-43 (2006), 5730–5742.
[31]
Hsueh-Ti Derek Liu, Francis Williams, Alec Jacobson, Sanja Fidler, and Or Litany. 2022. Learning Smooth Neural Functions via Lipschitz Regularization. In ACM SIGGRAPH 2022 Conference Proceedings (Vancouver, BC, Canada) (SIGGRAPH ’22). Association for Computing Machinery, New York, NY, USA, Article 31, 13 pages. https://doi.org/10.1145/3528233.3530713
[32]
Ran Luo, Tianjia Shao, Huamin Wang, Weiwei Xu, Xiang Chen, Kun Zhou, and Yin Yang. 2020. NNWarp: Neural Network-Based Nonlinear Deformation. IEEE Transactions on Visualization and Computer Graphics 26, 4 (2020), 1745–1759. https://doi.org/10.1109/TVCG.2018.2881451
[33]
Miles Macklin. 2022. Warp: A High-performance Python Framework for GPU Simulation and Graphics. https://github.com/nvidia/warp. NVIDIA GPU Technology Conference (GTC).
[34]
Laura Mainini and Karen Willcox. 2015. Surrogate modeling approach to support real-time structural assessment and decision making. AIAA Journal 53, 6 (2015), 1612–1626.
[35]
Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-Based Elastic Materials. ACM Transactions on Graphics (TOG) 30, 4, Article 72 (jul 2011), 8 pages. https://doi.org/10.1145/2010324.1964967
[36]
Lars Mescheder, Michael Oechsle, Michael Niemeyer, Sebastian Nowozin, and Andreas Geiger. 2019. Occupancy Networks: Learning 3D Reconstruction in Function Space. In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 4455–4465. https://doi.org/10.1109/CVPR.2019.00459
[37]
Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. 2021. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 65, 1 (dec 2021), 99–106. https://doi.org/10.1145/3503250
[38]
Rajaditya Mukherjee, Xiaofeng Wu, and Huamin Wang. 2016. Incremental Deformation Subspace Reconstruction. Comput. Graph. Forum 35, 7 (oct 2016), 169–178.
[39]
Shaowu Pan, Steven L. Brunton, and J. Nathan Kutz. 2023. Neural Implicit Flow: a mesh-agnostic dimensionality reduction paradigm of spatio-temporal data. Journal of Machine Learning Research 24, 41 (2023), 1–60. http://jmlr.org/papers/v24/22-0365.html
[40]
Zherong Pan, Hujun Bao, and Jin Huang. 2015. Subspace Dynamic Simulation Using Rotation-Strain Coordinates. ACM Transactions on Graphics (TOG) 34, 6, Article 242 (nov 2015), 12 pages. https://doi.org/10.1145/2816795.2818090
[41]
Jeong Joon Park, Peter Florence, Julian Straub, Richard Newcombe, and Steven Lovegrove. 2019. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
[42]
Alex Pentland and John Williams. 1989. Good vibrations: Modal dynamics for graphics and animation. In Proceedings of the 16th annual conference on Computer graphics and interactive techniques. 215–222.
[43]
Allan Pinkus. 2012. N-widths in Approximation Theory. Vol. 7. Springer Science & Business Media.
[44]
Charles R Qi, Hao Su, Kaichun Mo, and Leonidas J Guibas. 2017. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition. 652–660.
[45]
Maziar Raissi, Paris Perdikaris, and George Em Karniadakis. 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378 (2019), 686–707. https://doi.org/10.1016/j.jcp.2018.10.045
[46]
Cristian Romero, Dan Casas, Jesús Pérez, and Miguel Otaduy. 2021. Learning Contact Corrections for Handle-Based Subspace Dynamics. ACM Transactions on Graphics (TOG) 40, 4, Article 131 (jul 2021), 12 pages. https://doi.org/10.1145/3450626.3459875
[47]
David Ryckelynck. 2005. A priori hyperreduction method: an adaptive approach. J. Comput. Phys. 202, 1 (2005), 346–366. https://doi.org/10.1016/j.jcp.2004.07.015
[48]
Ahmed Shabana. 2012. Vibration of Discrete and Continuous Systems. Springer New York. https://books.google.ca/books?id=VfTxBwAAQBAJ
[49]
Tamar Rott Shaham, Michaël Gharbi, Richard Zhang, Eli Shechtman, and Tomer Michaeli. 2021. Spatially-Adaptive Pixelwise Networks for Fast Image Translation. In 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 14877–14886. https://doi.org/10.1109/CVPR46437.2021.01464
[50]
Nicholas Sharp, Cristian Romero, Alec Jacobson, Etienne Vouga, Paul G Kry, David IW Levin, and Justin Solomon. 2023. Data-Free Learning of Reduced-Order Kinematics. arXiv preprint arXiv:2305.03846 (2023).
[51]
Siyuan Shen, Yin Yang, Tianjia Shao, He Wang, Chenfanfu Jiang, Lei Lan, and Kun Zhou. 2021. High-Order Differentiable Autoencoder for Nonlinear Model Reduction. ACM Transactions on Graphics (TOG) 40, 4, Article 68 (jul 2021), 15 pages. https://doi.org/10.1145/3450626.3459754
[52]
Vincent Sitzmann, Julien N. P. Martel, Alexander W. Bergman, David B. Lindell, and Gordon Wetzstein. 2020. Implicit Neural Representations with Periodic Activation Functions. In Proceedings of the 34th International Conference on Neural Information Processing Systems (Vancouver, BC, Canada) (NIPS’20). Curran Associates Inc., Red Hook, NY, USA, Article 626, 12 pages.
[53]
Ivan Skorokhodov, Savva Ignatyev, and Mohamed Elhoseiny. 2021. Adversarial Generation of Continuous Images. In 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 10748–10759. https://doi.org/10.1109/CVPR46437.2021.01061
[54]
Breannan Smith, Fernando De Goes, and Theodore Kim. 2018. Stable Neo-Hookean Flesh Simulation. ACM Transactions on Graphics (TOG) 37, 2, Article 12 (mar 2018), 15 pages. https://doi.org/10.1145/3180491
[55]
Justin Solomon, Fernando De Goes, Gabriel Peyré, Marco Cuturi, Adrian Butscher, Andy Nguyen, Tao Du, and Leonidas Guibas. 2015. Convolutional wasserstein distances: Efficient optimal transportation on geometric domains. ACM Transactions on Graphics (ToG) 34, 4 (2015), 1–11.
[56]
Andrew M. Stuart and Antony R. Humphries. 1996. Dynamical Systems And Numerical Analysis.
[57]
Qingyang Tan, Zherong Pan, Lin Gao, and Dinesh Manocha. 2020. Realtime simulation of thin-shell deformable materials using CNN-based mesh embedding. IEEE Robotics and Automation Letters 5, 2 (2020), 2325–2332.
[58]
Adrien Treuille, Andrew Lewis, and Zoran Popović. 2006. Model reduction for real-time fluids. ACM Transactions on Graphics (TOG) 25, 3 (2006), 826–834.
[59]
Christoph von Tycowicz, Christian Schulz, Hans-Peter Seidel, and Klaus Hildebrandt. 2013. An Efficient Construction of Reduced Deformable Objects. ACM Transactions on Graphics (TOG) 32, 6, Article 213 (nov 2013), 10 pages. https://doi.org/10.1145/2508363.2508392
[60]
Steffen Wiewel, Moritz Becher, and Nils Thuerey. 2019. Latent space physics: Towards learning the temporal evolution of fluid flow. In Computer graphics forum, Vol. 38. Wiley Online Library, 71–82.
[61]
Karen Willcox and Jaime Peraire. 2002. Balanced model reduction via the proper orthogonal decomposition. AIAA journal 40, 11 (2002), 2323–2330.
[62]
Hongyi Xu and Jernej Barbič. 2016. Pose-Space Subspace Dynamics. ACM Transactions on Graphics (TOG) 35, 4, Article 35 (jul 2016), 14 pages. https://doi.org/10.1145/2897824.2925916
[63]
Hongyi Xu, Yijing Li, Yong Chen, and Jernej Barbič. 2015. Interactive material design using model reduction. ACM Transactions on Graphics (TOG) 34, 2 (2015), 1–14.
[64]
Guandao Yang, Serge Belongie, Bharath Hariharan, and Vladlen Koltun. 2021. Geometry Processing with Neural Fields. Advances in Neural Information Processing Systems 34 (2021).
[65]
Yin Yang, Dingzeyu Li, Weiwei Xu, Yuan Tian, and Changxi Zheng. 2015. Expediting precomputation for reduced deformable simulation. ACM Trans. Graph 34, 6 (2015).
[66]
Jonas Zehnder, Yue Li, Stelian Coros, and Bernhard Thomaszewski. 2021. Ntopo: Mesh-free topology optimization using implicit neural representations. Advances in Neural Information Processing Systems 34 (2021), 10368–10381.
[67]
Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv preprint arXiv:1605.04797 (2016).