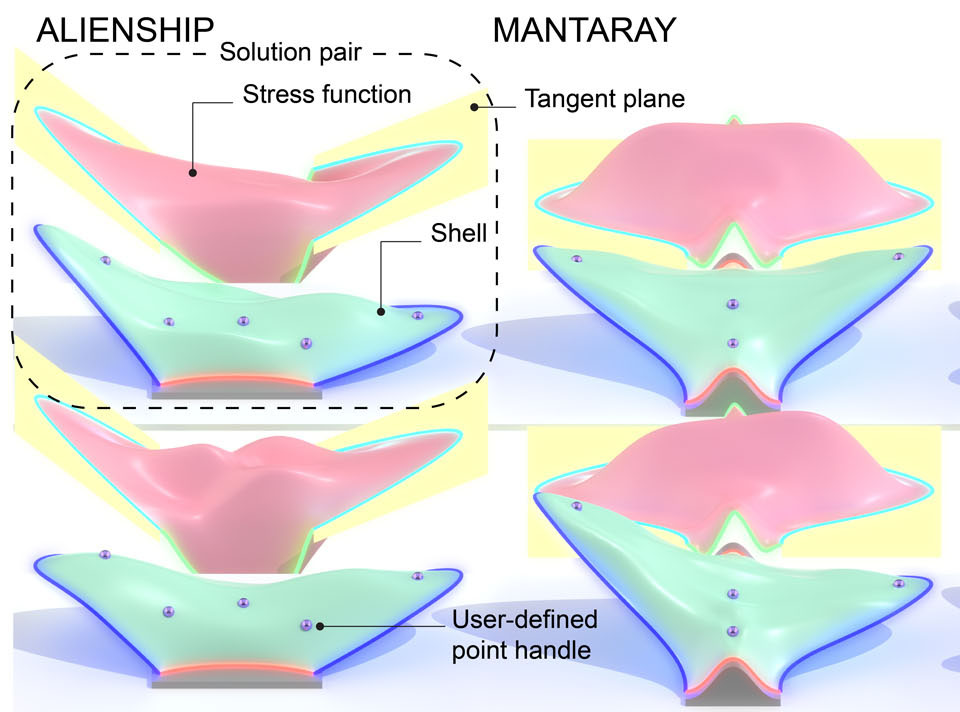
“Interactive Exploration of Tension-Compression Mixed Shells” by Miki and Mitchell
Conference:
Type(s):
Title:
- Interactive Exploration of Tension-Compression Mixed Shells
Session/Category Title:
- Everything Interactive and Dynamic
Presenter(s)/Author(s):
Abstract:
Achieving a pure-compression stress state is considered central to the form-finding of shell structures. However, the pure-compression assumption restricts the geometry of the structure’s plan in that any free boundary edges cannot bulge outward. Allowing both tension and compression is essential so that overhanging leaves can stretch out toward the sky. When performing tension-compression mixed form-finding, a problem with boundary condition (BC) compatibility arises. Since the form-finding equation is hyperbolic, boundary information propagates along the asymptotic lines of the stress function. If conflicting BC data is prescribed at either end of an asymptotic line, the problem becomes ill-posed. This requires a user of a form-finding method to know the solution in advance. By contrast, pure-tension or pure-compression problems are elliptic and always give solutions under any BCs sufficient to restrain rigid motion. To solve the form-finding problem for tension-compression mixed shells, we focus on the Airy’s stress function, which describes the stress field in a shell. Rather than taking the stress function as given, we instead treat both the stress function and the shell as unknowns. This doubles the solution variables, turning the problem to one that has an infinity of different solutions. By enforcing equilibrium in the shell interior and prescribing the correct matching pairs of BCs to both the stress function and the shell, a stress function and shell can be simultaneously found such that equilibrium is satisfied everywhere in the shell interior and thus automatically has compatible BCs by construction. The problem of a potentially over-constrained form-finding is thus avoided by expanding the solution space and creating an under-determined problem. By varying inputs and repeatedly searching for stress function-shell pairs that fall within the solution space, a user is allowed to interactively explore the possible forms of tension-compression mixed shells under the given plan of the shell.
References:
1. George Biddell Airy. 1862. On the Strains in the Interior of Beams. Proceedings of the Royal Society of London 12 (1862), 304–306.
2. T. Amaranath. 2009. An Elementary Course in Partial Differential Equations. Jones & Bartlett Learning, Ontario, Canada.
3. Maurizio Angelillo, Enrico Babilio, and Antonio Fortunato. 2013. Singular stress fields for masonry-like vaults. Continuum Mechanics and Thermodynamics 25, 2–4 (2013), 423–441.
4. Anna M Bauer, Roland Wüchner, and Kai-Uwe Bletzinger. 2018. Innovative CAD-integrated isogeometric simulation of sliding edge cables in lightweight structures. Journal of the International Association for Shell and Spatial Structures 59, 4 (2018), 251–258.
5. Philippe Block and John Ochsendorf. 2007. Thrust network analysis: a new methodology for three-dimensional equilibrium. Journal of the International Association for Shell and Spatial Structures 48, 3 (2007), 167–173.
6. Philippe Block, Tom Van Mele, Matthias Rippmann, and Noelle Paulson. 2017. Beyond Bending: Reimagining Compression Shells. Edition Detail, Munuch, Germany.
7. M Breitenberger, A Apostolatos, B Philipp, R Wüchner, and K-U Bletzinger. 2015. Analysis in computer aided design: Nonlinear isogeometric B-Rep analysis of shell structures. Computer Methods in Applied Mechanics and Engineering 284 (2015), 401–457.
8. Yu-Chou Chiang and Andrew Borgart. 2022. A form-finding method for membrane shells with radial basis functions. Engineering Structures 251 (2022), 113514.
9. Pál Csonka. 1987. Theory and practice of membrane shells. VDI Verlag, Düsseldorf, Germany.
10. Fernando de Goes, Pierre Alliez, Houman Owhadi, and Mathieu Desbrun. 2013. On the equilibrium of simplicial masonry structures. ACM Transactions on Graphics (TOG) 32, 4, Article 93 (jul 2013), 10 pages.
11. Lars Eldén and Salman Ahmadi-Asl. 2019. Solving bilinear tensor least squares problems and application to Hammerstein identification. Numerical Linear Algebra with Applications 26, 2 (2019), e2226.
12. G. Evans, J. Blackledge, and P. Yardley. 2012. Numerical Methods for Partial Differential Equations. Springer, London.
13. Fernando Fraternali, Maurizio Angelillo, and Antonio Fortunato. 2002. A lumped stress method for plane elastic problems and the discrete-continuum approximation. International journal of solids and structures 39, 25 (2002), 6211–6240.
14. Albert Edward Green and Wolfgang Zerna. 1968. Theoretical elasticity. Oxford University Press, London.
15. Yujie Guo, Jason Heller, Thomas JR Hughes, Martin Ruess, and Dominik Schillinger. 2018. Variationally consistent isogeometric analysis of trimmed thin shells at finite deformations, based on the STEP exchange format. Computer Methods in Applied Mechanics and Engineering 336 (2018), 39–79.
16. Uwe Harlander and Leo RM Maas. 2007. Two alternatives for solving hyperbolic boundary value problems of geophysical fluid dynamics. Journal of Fluid Mechanics 588 (2007), 331–351.
17. Thomas JR Hughes, John A Cottrell, and Yuri Bazilevs. 2005. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering 194, 39–41 (2005), 4135–4195.
18. Axel Kilian and John Ochsendorf. 2005. Particle-spring systems for structural form finding. Journal of the international association for shell and spatial structures 46, 2 (2005), 77–84.
19. Hyun-Jung Kim, Yu-Deok Seo, and Sung-Kie Youn. 2009. Isogeometric analysis for trimmed CAD surfaces. Computer Methods in Applied Mechanics and Engineering 198, 37–40 (2009), 2982–2995.
20. Young W Kwon and Hyochoong Bang. 2018. The finite element method using MATLAB. CRC press, Florida, USA.
21. Yang Liu, Hao Pan, John Snyder, Wenping Wang, and Baining Guo. 2013. Computing self-supporting surfaces by regular triangulation. ACM Transactions on Graphics (TOG) 32, 4, Article 92 (jul 2013), 10 pages.
22. Masaaki Miki, Emil Adiels, William Baker, Toby Mitchell, Alexander Sehlström, and Chris J. K. Williams. 2022. Form-finding of shells containing both tension and compression using the Airy stress function. International Journal of Space Structures (June 2022).
23. Masaaki Miki, Takeo Igarashi, and Philippe Block. 2015. Parametric self-supporting surfaces via direct computation of airy stress functions. ACM Transactions on Graphics (TOG) 34, 4, Article 89 (jul 2015), 12 pages.
24. Philip M Morse and Herman Feshbach. 1954. Difference Equations and Boundary Conditions. In Methods of theoretical physics Part I (international student ed.). McGraw-Hill, NewYork, Chapter 6.2, 692–706.
25. Carlo Olivieri, Maurizio Angelillo, Antonio Gesualdo, Antonino Iannuzzo, and Antonio Fortunato. 2021. Parametric design of purely compressed shells. Mechanics of Materials 155 (2021), 103782.
26. Daniele Panozzo, Philippe Block, and Olga Sorkine-Hornung. 2013. Designing unreinforced masonry models. ACM Transactions on Graphics (TOG) 32, 4, Article 91 (jul 2013), 12 pages.
27. Daniel Piker. 2013. Kangaroo: form finding with computational physics. Architectural Design 83, 2 (2013), 136–137.
28. Helmut Pottmann, Andreas Asperl, Michael Hofer, and Axel Kilian. 2008. Architectural Geometry. Bentley Institute Press.
29. A Pucher. 1938. Die Berechnung der Dehnungsspannungen von Rotationsschalen mit Hilfe von Spannungsfunktionen. Int. Vereinig. Brücken-u. Hochbau Abh 5 (1938), 275.
30. Evariste Sanchez-Palencia, Olivier Millet, and Fabien Béchet. 2010. Singular problems in shell theory: computing and asymptotics. Lecture Notes in Applied and Computational Mechanics. Vol. 54. Springer-Verlag, Berlin.
31. Robert Schmidt, Roland Wüchner, and Kai-Uwe Bletzinger. 2012. Isogeometric analysis of trimmed NURBS geometries. Computer Methods in Applied Mechanics and Engineering 241 (2012), 93–111.
32. Chengcheng Tang, Xiang Sun, Alexandra Gomes, Johannes Wallner, and Helmut Pottmann. 2014. Form-finding with polyhedral meshes made simple. ACM Transactions on Graphics (TOG) 33, 4 (2014), 1–9.
33. Stephen P Timoshenko and Sergius Woinowsky-Krieger. 1959. Theory of plates and shells. McGraw-hill, New York.
34. Etienne Vouga, Mathias Höbinger, Johannes Wallner, and Helmut Pottmann. 2012. Design of self-supporting surfaces. ACM Transactions on Graphics (TOG) 31, 4, Article 87 (jul 2012), 11 pages.
35. CJK Williams. 1990. Generation of a class of structural forms for vaults and sails. Structural Engineer 68, 12 (1990), 231–235.
36. Yang Xia, Angelos Mantzaflaris, Bert Jüttler, Hao Pan, Ping Hu, and Wenping Wang. 2019. Design of self-supporting surfaces with isogeometric analysis. Computer Methods in Applied Mechanics and Engineering 353 (2019), 328–347.