“Geostatistical motion interpolation”

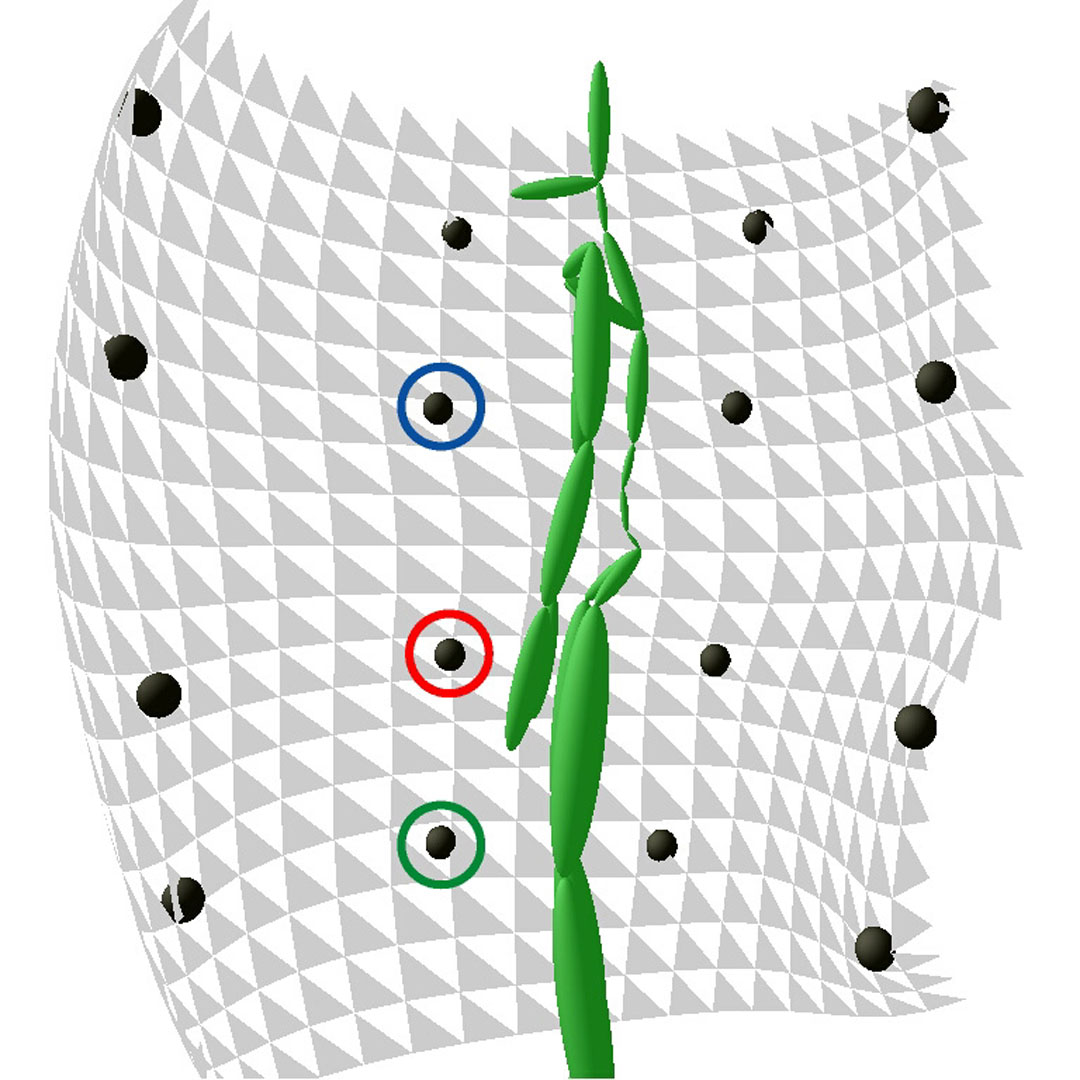
A common motion interpolation technique for realistic human animation is to blend similar motion samples with weighting functions whose parameters are embedded in an abstract space. Existing methods, however, are insensitive to statistical properties, such as correlations between motions. In addition, they lack the capability to quantitatively evaluate the reliability of synthesized motions. This paper proposes a method that treats motion interpolations as statistical predictions of missing data in an arbitrarily definable parametric space. A practical technique of geostatistics, called universal kriging, is then introduced for statistically estimating the correlations between the dissimilarity of motions and the distance in the parametric space. Our method statistically optimizes interpolation kernels for given parameters at each frame, using a pose distance metric to efficiently analyze the correlation. Motions are accurately predicted for the spatial constraints represented in the parametric space, and they therefore have few undesirable artifacts, if any. This property alleviates the problem of spatial inconsistencies, such as foot-sliding, that are associated with many existing methods. Moreover, numerical estimates for the reliability of predictions enable motions to be adaptively sampled. Since the interpolation kernels are computed with a linear system in real-time, motions can be interactively edited using various spatial controls.

1. Abe, Y., Liu, C. K., and Popović, Z. 2004. Momentum-based parameterization of dynamic character motion. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation 2004, 173–182. Google ScholarDigital Library
2. Alexa, M., and Muller, W. 2000. Representing animations by principal components. Computer Graphics Forum 19, 3, 411–418.Google ScholarCross Ref
3. Arikan, O., Forsyth, D. A., and O’Brien, J. F. 2003. Motion synthesis from annotations. ACM Transactions on Graphics 22, 3, 402–408. Google ScholarDigital Library
4. Bruderlin, A., and Williams, L. 1995. Motion signal processing. In Proc. of SIGGRAPH 95, 97–104. Google ScholarDigital Library
5. Cressie, N. A., and Hawkins, D. M. 1980. Robust estimation of the variogram. Mathematical Geology 12, 115–125.Google ScholarCross Ref
6. Cressie, N. A. 1985. Fitting variogram models by weighted least squares. Mathematical Geology 17, 563–586.Google ScholarCross Ref
7. Cressie, N. A. 1993. Statistics for Spatial Data. Wiley-Interscience.Google Scholar
8. De Juan, C., and Bodenheimer, B. 2004. Cartoon textures. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 267–276. Google ScholarDigital Library
9. Grochow, K., Martin, S. L., Hertzmann, A., and Popović, Z. 2004. Style-based inverse kinematics. ACM Transactions on Graphics 23, 3, 522–531. Google ScholarDigital Library
10. Huijbregts. C. J., and Matheron. G. 1971. Universal kriging. In Proc. of International Symposium on Techniques for Decision-Making in Mineral Industry, 159–169.Google Scholar
11. Ikemoto, L., and Forsyth. D. A. 2004. Enriching a motion collection by transplanting limbs. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation 2004. 99–108. Google ScholarDigital Library
12. Journel, A. G., and Huijbregts. C. J. 1978. Mining Geostatistics. Academic Press.Google Scholar
13. Kovar, L., and Gleicher, M. 2002. Motion graphs. ACM Transactions on Graphics 21, 3, 473–482. Google ScholarDigital Library
14. Kovar, L., and Gleicher, M. 2003. Flexible automatic motion blending with registration curves. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 214–224. Google ScholarDigital Library
15. Kovar, L., and Gleicher, M. 2004. Automated extraction and parameterization of motions in large data sets. ACM Transactions on Graphics 23, 3, 559–568. Google ScholarDigital Library
16. Kovar, L., Schreiner, J., and Gleicher, M. 2002. Footskate cleanup for motion capture editing. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 97–194. Google ScholarDigital Library
17. Lee, J., Chai, J., Reitsma, P. S. A., Hodgins, J. K., and Pollard, N. S. 2002. Interactive control of avatars animated with human motion data. ACM Transaction on Graphics 21, 3, 491–500. Google ScholarDigital Library
18. Park, S. I., Shin, H. J., Kim, T. H., and Shin, S. Y. 2004. On-line motion blending for real-time locomotion generation. Computer Animation and Virtual Worlds 15, 3–4, 125–138. Google ScholarDigital Library
19. Rose, C., Bodenheimer, B., and Cohen, M. F. 1998. Verbs and adverbs: Multidimensional motion interpolation. IEEE Computer Graphics and Applications 18, 5, 32–40. Google ScholarDigital Library
20. Rose, C. F., Sloan, P.-P. J., and Cohen, M. F. 2001. Artist directed inverse-kinematics using radial basis function interpolation. Computer Graphics Forum 20, 3, 239–250.Google ScholarCross Ref
21. Safonova, A., Hodgins, J. K., and Pollard, N. S. 2004. Synthesizing physically realistic human motion in low-dimensional, behavior-specific spaces. ACM Transactions on Graphics 23, 3, 514–521. Google ScholarDigital Library
22. Sakamoto, Y., and Kuriyama, S. 2004. Motion map: Image-based retrieval and segmentation of motion data. In Proc. of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 259–266. Google ScholarDigital Library
23. Tanco, L. M., and Hilton, A. 2000. Realistic synthesis of novel human movements from a database of motion capture examples. In Proc. of Workshop on Human Motion. 137–142. Google ScholarDigital Library
24. Unuma, M., Anjyo, K., and Takeuchi, R. 1995. Fourier principles for emotion-based human figure animation. In Proc. of SIGGRAPH 95, 91–96. Google ScholarDigital Library
25. Wackernagel, H. 2003. Multivariate Geostatistics. Springer-Verlag.Google Scholar
26. Wiley, D. J., and Hahn, J. K. 1997. Interpolation synthesis of articulated figure motion. IEEE Computer Graphics and Applications 17, 6, 39–45. Google ScholarDigital Library