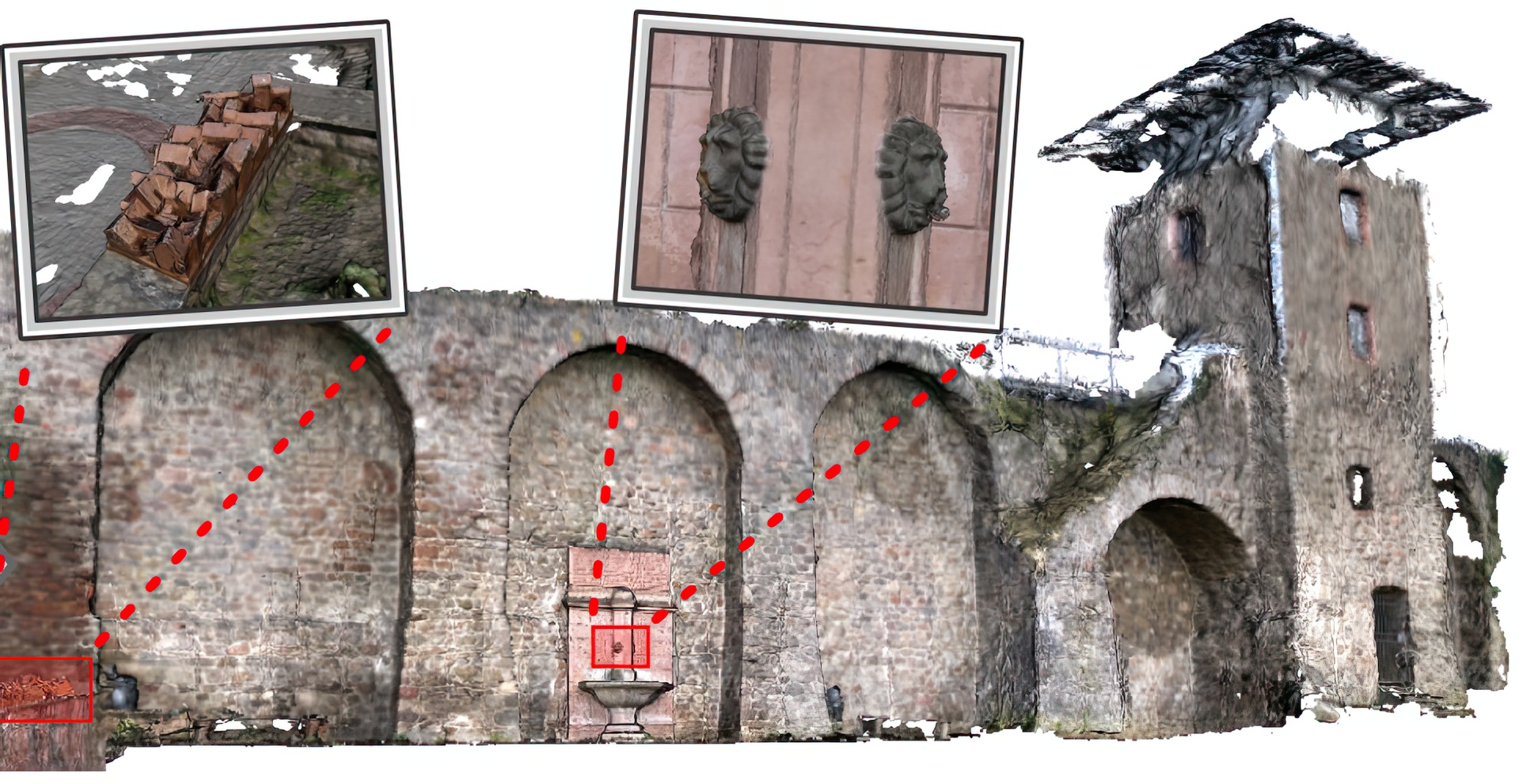
“Fusion of depth maps with multiple scales”
Conference:
Type(s):
Title:
- Fusion of depth maps with multiple scales
Session/Category Title: 3D Capture and Reconstruction
Presenter(s)/Author(s):
Abstract:
Multi-view stereo systems can produce depth maps with large variations in viewing parameters, yielding vastly different sampling rates of the observed surface. We present a new method for surface reconstruction by integrating a set of registered depth maps with dramatically varying sampling rate. The method is based on the construction of a hierarchical signed distance field represented in an incomplete primal octree by incrementally adding triangulated depth maps. Due to the adaptive data structure, our algorithm is able to handle depth maps with varying scale and to consistently represent coarse, low-resolution regions as well as small details contained in high-resolution depth maps. A final surface mesh is extracted from the distance field by construction of a tetrahedral complex from the scattered signed distance values and applying the Marching Tetra-hedra algorithm on the partition. The output is an adaptive triangle mesh that seamlessly connects coarse and highly detailed regions while avoiding filling areas without suitable input data.
References:
1. Agarwal, S., Snavely, N., Simon, I., Seitz, S. M., and Szeliski, R. 2009. Building Rome in a day. In Proc. ICCV, 72–79.Google Scholar
2. Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D., and Silva, C. T. 2001. Point set surfaces. In Proc. VIS, 21–28. Google ScholarDigital Library
3. Alliez, P., Cohen-steiner, D., Tong, Y., and Desbrun, M. 2007. Voronoi-based variational reconstruction of unoriented point sets. In Proc. SGP, 39–48. Google ScholarDigital Library
4. Boissonnat, J.-D., and Oudot, S. 2005. Provably good sampling and meshing of surfaces. Graphical Models 67, 405–451. Google ScholarDigital Library
5. Chen, Y., and Medioni, G. 1991. Object modeling by registration of multiple range images. In Proc. ICRA, 2724–2729.Google Scholar
6. Curless, B., and Levoy, M. 1996. A volumetric method for building complex models from range images. In Proc. SIGGRAPH, 303–312. Google ScholarDigital Library
7. Doi, A., and Koide, A. 1991. An efficient method of triangulating equi-valued surfaces by using tetrahedral cells. IEICE Trans. E74, 1, 214–224.Google Scholar
8. Frahm, J.-M., Georgel, P., Gallup, D., Johnson, T., Raguram, R., Wu, C., Jen, Y.-H., Dunn, E., Clipp, B., Lazebnik, S., and Pollefeys, M. 2010. Building Rome on a cloudless day. In Proc. ECCV, 368–381. Google ScholarDigital Library
9. Goesele, M., Snavely, N., Curless, B., Hoppe, H., and Seitz, S. M. 2007. Multi-view stereo for community photo collections. In Proc. ICCV.Google Scholar
10. Gortler, S. J., Grzeszczuk, R., Szeliski, R., and Cohen, M. F. 1996. The lumigraph. In Proc. SIGGRAPH, 43–54. Google ScholarDigital Library
11. Guennebaud, G., and Gross, M. 2007. Algebraic point set surfaces. In Proc. SIGGRAPH. Google ScholarDigital Library
12. Higuchi, K., Hebert, M., and Ikeuchi, K. 1994. Building 3D models from unregistered range images. In Proc. ICRA, 2248–2253.Google Scholar
13. Hilton, A., and Illingworth, J. 1997. Multi-resolution geometric fusion. In Proc. 3DIM, 181–188. Google ScholarDigital Library
14. Hilton, A., Stoddart, A., Illingworth, J., and Windeatt, T. 1996. Reliable surface reconstruction from multiple range images. In Proc. ECCV. 117–126. Google ScholarDigital Library
15. Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and Stuetzle, W. 1992. Surface reconstruction from unorganized points. In Proc. SIGGRAPH, 71–78. Google ScholarDigital Library
16. Ju, T., Losasso, F., Schaefer, S., and Warren, J. 2002. Dual contouring of hermite data. In Proc. SIGGRAPH, 339–346. Google ScholarDigital Library
17. Kazhdan, M., Bolitho, M., and Hoppe, H. 2006. Poisson surface reconstruction. In Proc. SGP, 61–70. Google ScholarDigital Library
18. Kazhdan, M., Klein, A., Dalal, K., and Hoppe, H. 2007. Unconstrained isosurface extraction on arbitrary octrees. In Proc. SGP, 125–133. Google ScholarDigital Library
19. Levin, D. 1998. The approximation power of moving least-squares. Mathematics of Computation 67, 1517–1531. Google ScholarDigital Library
20. Levoy, M., 2011. Range data versus 3D models – a caveat on the use of these models. http://graphics.stanford.edu/data/3Dscanrep/.Google Scholar
21. Lindeberg, T. 1998. Feature detection with automatic scale selection. International Journal of Computer Vision 30, 2, 79–116. Google ScholarDigital Library
22. Lorensen, W., and Cline, H. 1987. Marching Cubes: a high resolution 3D surface construction algorithm. Proc. SIGGRAPH 21, 5, 79–86. Google ScholarDigital Library
23. Mitchell, D. P. 1987. Generating antialiased images at low sampling densities. In Proc. SIGGRAPH, 65–72. Google ScholarDigital Library
24. Ohtake, Y., Belyaev, A., and Seidel, H.-P. 2006. Sparse surface reconstruction with adaptive partition of unity and radial basis functions. Graphical Models 68, 1, 15–24. Google ScholarDigital Library
25. Pito, R. 1996. Mesh integration based on co-measurements. In Proc. ICIP, 397–400.Google ScholarCross Ref
26. Schaefer, S., and Warren, J. 2005. Dual marching cubes: Primal contouring of dual grids. Computer Graphics Forum 24, 195–201.Google ScholarCross Ref
27. Schroeder, W. J., Geveci, B., and Malaterre, M. 2004. Compatible triangulations of spatial decompositions. In Proc. VIS, 211–218. Google ScholarDigital Library
28. Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and Szeliski, R. 2006. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proc. CVPR, 519–528. Google ScholarDigital Library
29. Snavely, N., Seitz, S. M., and Szeliski, R. 2008. Skeletal sets for efficient structure from motion. In Proc. CVPR.Google Scholar
30. Soucy, M., and Laurendeau, D. 1992. Multi-resolution surface modeling from multiple range views. In Proc. CVPR, 348–353.Google Scholar
31. Turk, G., and Levoy, M. 1994. Zippered polygon meshes from range images. In Proc. SIGGRAPH, 311–318. Google ScholarDigital Library
32. Zach, C., Pock, T., and Bischof, H. 2007. A globally optimal algorithm for robust TV-L1 range image integration. In Proc. ICCV.Google Scholar