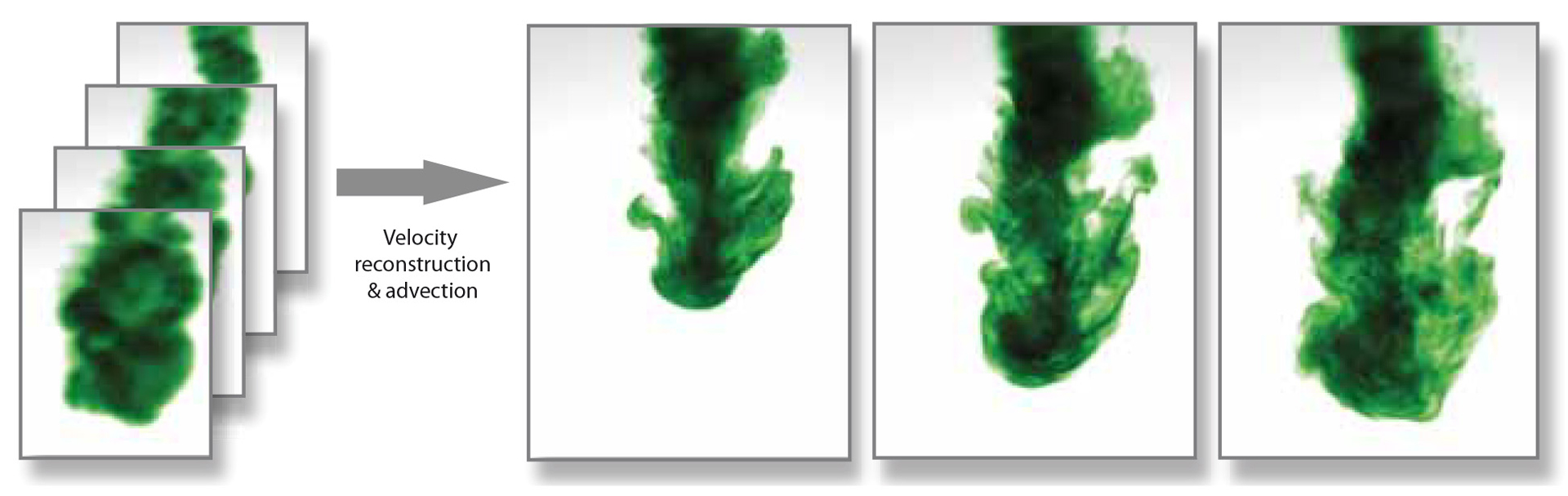
“From capture to simulation: connecting forward and inverse problems in fluids” by Gregson, Ihrke, Thuerey and Heidrich
Conference:
Type(s):
Title:
- From capture to simulation: connecting forward and inverse problems in fluids
Session/Category Title: Fluids
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We explore the connection between fluid capture, simulation and proximal methods, a class of algorithms commonly used for inverse problems in image processing and computer vision. Our key finding is that the proximal operator constraining fluid velocities to be divergence-free is directly equivalent to the pressure-projection methods commonly used in incompressible flow solvers. This observation lets us treat the inverse problem of fluid tracking as a constrained flow problem all while working in an efficient, modular framework. In addition it lets us tightly couple fluid simulation into flow tracking, providing a global prior that significantly increases tracking accuracy and temporal coherence as compared to previous techniques. We demonstrate how we can use these improved results for a variety of applications, such as re-simulation, detail enhancement, and domain modification. We furthermore give an outlook of the applications beyond fluid tracking that our proximal operator framework could enable by exploring the connection of deblurring and fluid guiding.
References:
1. Akinci, N., Ihmsen, M., Akinci, G., Solenthaler, B., and Teschner, M. 2012. Versatile Rigid-fluid Coupling for Incompressible SPH. ACM Transactions on Graphics 31, 4, article 62. Google ScholarDigital Library
2. Ando, R., Thuerey, N., and Wojtan, C. 2013. Highly Adaptive Liquid Simulations on Tetrahedral Meshes. ACM Transactions on Graphics 32, 4 (August), article 10. Google ScholarDigital Library
3. Atcheson, B., Ihrke, I., Heidrich, W., Tevs, A., Bradley, D., Magnor, M., and Seidel, H.-P. 2008. Time-resolved 3D Capture of Non-stationary Gas Flows. ACM Transactions on Graphics 27, 5, article 132. Google ScholarDigital Library
4. Barbu, I., Herzet, C., and Mémin, E. 2013. Joint Estimation of Volume and Velocity in TomoPIV. In International Symposium on Particle Image Velocimetry.Google Scholar
5. Batty, C., Bertails, F., and Bridson, R. 2007. A fast variational framework for accurate solid-fluid coupling. ACM Transactions on Graphics 26, 3 (July). Google ScholarDigital Library
6. Bridson, R. 2008. Fluid Simulation for Computer Graphics. AK Peters/CRC Press. Google ScholarDigital Library
7. Elsinga, G., Scarano, F., Wieneke, B., and van Oudheusden, B. 2006. Tomographic Particle Image Velocimetry. Experiments in Fluids 41, 6, 933–947.Google ScholarCross Ref
8. Foster, N., and Metaxas, D. 1996. Realistic Animation of Liquids. Graphical Models and Image Processing 58, 5 (Sept.), 471–483. Google ScholarDigital Library
9. Gregson, J., Krimerman, M., Hullin, M. B., and Heidrich, W. 2012. Stochastic Tomography and its Applications in 3D Imaging of Mixing Fluids. Proceedings ACM SIGGRAPH 2012 31, 4, article 52. Google ScholarDigital Library
10. Gu, J., Nayar, S., Grinspun, E., Belhumeur, P., and Ramamoorthi, R. 2013. Compressive Structured Light for Recovering Inhomogeneous Participating Media. IEEE Pattern Analysis and Machine Intelligence 35, 3, 555–567.Google Scholar
11. Harlow, F., and Welch, E. 1965. Numerical Calculation of Time-dependent Viscous Incompressible Flow of Fluid with Free Surface. Physics of Fluids 8, 12, 2182–2189.Google ScholarCross Ref
12. Hasinoff, S. W., and Kutulakos, K. N. 2007. Photo-consistent Reconstruction of Semitransparent Scenes by Density-sheet Decomposition. IEEE Trans. PAMI 29, 5, 870–885. Google ScholarDigital Library
13. Hawkins, T., Einarsson, P., and Debevec, P. 2005. Acquisition of Time-Varying Participating Media. ACM Transactions on Graphics 24, 3, 812–815. Google ScholarDigital Library
14. Horn, B., and Schunck, B. 1981. Determining Optical Flow. Artificial Intelligence 17, 1, 185–203.Google ScholarDigital Library
15. Ihrke, I., and Magnor, M. 2004. Image-Based Tomographic Reconstruction of Flames. In Proc. of ACM/Eurographics Symposium on Computer Animation (SCA), 367–375. Google ScholarDigital Library
16. Kadri Harouna, S., Dérian, P., Héas, P., and Memin, E. 2013. Divergence-free Wavelets and High Order Regularization. International Journal of Computer Vision 103, 1 (May), 80–99.Google ScholarCross Ref
17. Kim, B., Liu, Y., Llamas, I., and Rossignac, J. 2005. Flow-Fixer: Using BFECC for Fluid Simulation. In Proceedings of the First Eurographics conference on Natural Phenomena, 51–56. Google ScholarDigital Library
18. Kim, T., Thürey, N., James, D., and Gross, M. 2008. Wavelet Turbulence for Fluid Simulation. ACM Transactions on Graphics 27, 3, article 50. Google ScholarDigital Library
19. Li, C., Pickup, D., Saunders, T., Cosker, D., Marshall, D., Hall, P., and Willis, P. 2013. Water Surface Modeling from a Single Viewpoint Video. IEEE Transactions on Visualization and Computer Graphics 19, 7, 1242–1251. Google ScholarDigital Library
20. Liu, T., and Shen, L. 2008. Fluid Flow and Optical Flow. Journal of Fluid Mechanics 614 (11), 253–291.Google ScholarCross Ref
21. McNamara, A., Treuille, A., Popović, Z., and Stam, J. 2004. Fluid Control Using the Adjoint Method. ACM Transactions on Graphics 23, 3, 449–456. Google ScholarDigital Library
22. Meinhardt-Llopis, E., Pérez, J. S., and Kondermann, D. 2013. Horn-Schunck Optical Flow with a Multi-Scale Strategy. Image Processing On-Line 2013, 151–172.Google ScholarCross Ref
23. Müller, M., Charypar, D., and Gross, M. 2003. Particle-based Fluid Simulation for Interactive Applications. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 154–159. Google ScholarDigital Library
24. Narain, R., Sewall, J., Carlson, M., and Lin, M. C. 2008. Fast Animation of Turbulence Using Energy Transport and Procedural Synthesis. ACM Transactions on Graphics 27, 5, article 166. Google ScholarDigital Library
25. Nielsen, M. B., Christensen, B. B., Zafar, N. B., Roble, D., and Museth, K. 2009. Guiding of Smoke Animations through Variational Coupling of Simulations at Different Resolutions. In Proceedings of the ACM SIGGRAPH/Eurographics symposium on Computer animation, 217–226. Google ScholarDigital Library
26. Panigrahi, P. K., and Muralidhar, K. 2012. Schlieren and Shadowgraph Methods in Heat and Mass Transfer. Springer.Google Scholar
27. Parikh, N., and Boyd, S. 2013. Proximal Algorithms. Foundations and Trends in Optimization 1, 3, 123–231.Google Scholar
28. Pfaff, T., and Thuerey, N., 2013. MantaFlow. http://mantaflow.ethz.ch.Google Scholar
29. Settles, G. S. 2001. Schlieren and Shadowgraph Techniques. Experimental Fluid Mechanics. Springer.Google Scholar
30. Shi, L., and Yu, Y. 2005. Taming Liquids for Rapidly Changing Targets. In Proceedings of the ACM SIGGRAPH/Eurographics symposium on Computer animation, 229–236. Google ScholarDigital Library
31. Stam, J. 1999. Stable Fluids. In Proceedings ACM SIGGRAPH, 121–128. Google ScholarDigital Library
32. Stomakhin, A., Schroeder, C., Chai, L., Teran, J., and Selle, A. 2013. A Material Point Method for Snow Simulation. ACM Transactions on Graphics 32, 4, article 102. Google ScholarDigital Library
33. Su, L. K., and Dahm, W. J. A. 1996. Scalar Imaging Velocimetry Measurements of the Velocity Gradient Tensor Field in Turbulent Flows. I. Assessment of Errors. Physics of Fluids 8, 7, 1869–1882.Google Scholar
34. Sun, D., Roth, S., and Black, M. J. 2014. A Quantitative Analysis of Current Practices in Optical Flow Estimation and the Principles behind Them. International Journal of Computer Vision 106, 2, 115–137. Google ScholarDigital Library
35. Thuerey, N., Keiser, R., Ruede, U., and Pauly, M. 2006. Detail-Preserving Fluid Control. In Proceedings of the ACM SIGGRAPH/Eurographics symposium on Computer animation, 7–12. Google ScholarDigital Library
36. Tropea, C., Yarin, A. L., and Foss, J. F. 2006. Handbook of Experimental Fluid Mechanics. Springer.Google Scholar
37. Van Vliet, E., Van Bergen, S., Derksen, J., Portela, L., and Van den Akker, H. 2004. Time-Resolved, 3D, Laser-Induced Fluorescence Measurements of Fine-Structure Passive Scalar Mixing in a Tubular Reactor. Experiments in Fluids 37, 1–21.Google ScholarCross Ref
38. Vlasenko, A., and Schnörr, C. 2009. Variational Approaches to Image Fluid Flow Estimation with Physical Priors. In Imaging Measurement Methods for Flow Analysis, vol. 106. Springer, 247–256.Google Scholar
39. Wang, H., Liao, M., Zhang, Q., Yang, R., and Turk, G. 2009. Physically Guided Liquid Surface Modeling from Videos. ACM Transactions on Graphics 28, 3, article 90. Google ScholarDigital Library
40. Yuan, J., Schnörr, C., and Mémin, E. 2007. Discrete Orthogonal Decomposition and Variational Fluid Flow Estimation. Journal of Mathemathical Imaging and Vision 28, 1, 67–80. Google ScholarDigital Library
41. Zhu, Y., and Bridson, R. 2005. Animating Sand as a Fluid. ACM Transactions on Graphics 24, 3, 965–972. Google ScholarDigital Library