“Fast and robust mesh arrangements using floating-point arithmetic” by Cherchi, Livesu, Scateni and Attene
Conference:
Type(s):
Title:
- Fast and robust mesh arrangements using floating-point arithmetic
Session/Category Title:
- Meticulous Meshes
Presenter(s)/Author(s):
Abstract:
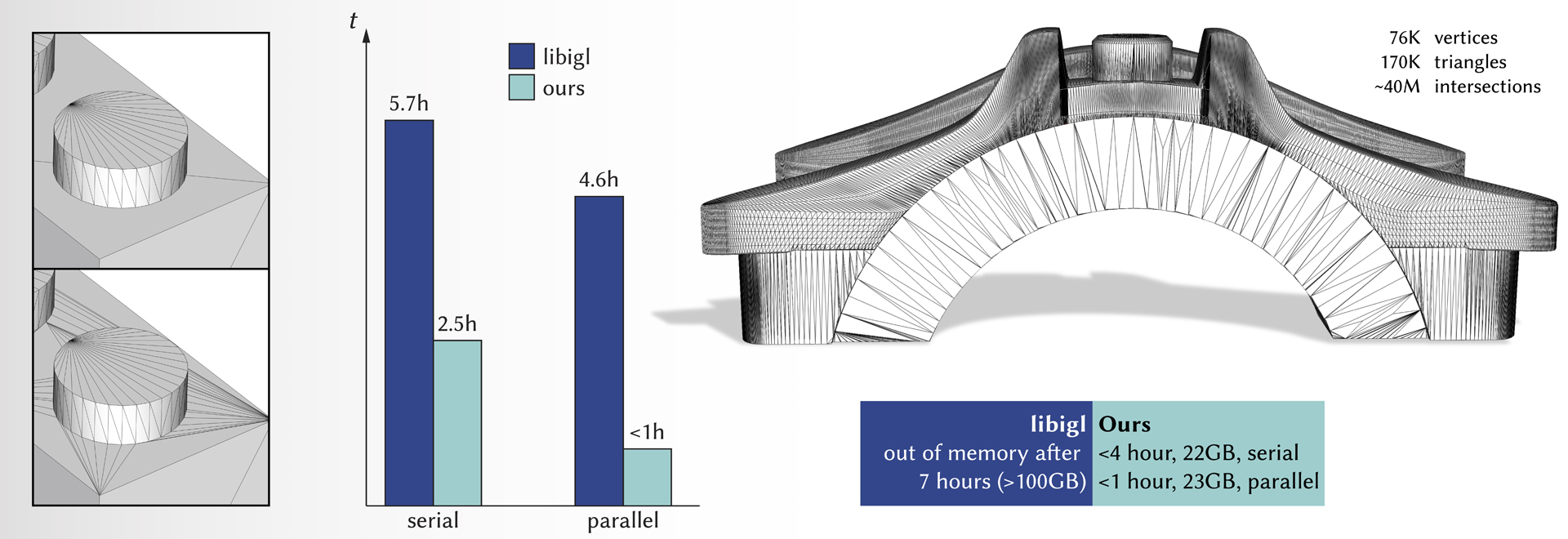
We introduce a novel algorithm to transform any generic set of triangles in 3D space into a well-formed simplicial complex. Intersecting elements in the input are correctly identified, subdivided, and connected to arrange a valid configuration, leading to a topologically sound partition of the space into piece-wise linear cells. Our approach does not require the exact coordinates of intersection points to calculate the resulting complex. We represent any intersection point as an unevaluated combination of input vertices. We then extend the recently introduced concept of indirect predicates [Attene 2020] to define all the necessary geometric tests that, by construction, are both exact and efficient since they fully exploit the floating-point hardware. This design makes our method robust and guaranteed correct, while being virtually as fast as non-robust floating-point based implementations. Compared with existing robust methods, our algorithm offers a number of advantages: it is much faster, has a better memory layout, scales well on extremely challenging models, and allows fully exploiting modern multi-core hardware with a parallel implementation. We thoroughly tested our method on thousands of meshes, concluding that it consistently outperforms prior art. We also demonstrate its usefulness in various applications, such as computing efficient mesh booleans, Minkowski sums, and volume meshes.
References:
1. Chrystiano Araújo, Daniela Cabiddu, Marco Attene, Marco Livesu, Nicholas Vining, and Alla Sheffer. 2019. Surface2Volume: Surface Segmentation Conforming Assemblable Volumetric Partition. ACM Transaction on Graphics 38, 4 (2019). Google ScholarDigital Library
2. Marco Attene. 2010. A lightweight approach to repair polygon meshes. The Visual Computer (2010), 1393–1406.Google Scholar
3. Marco Attene. 2014. Direct repair of self-intersecting meshes. Graphical Models 76, 6 (2014), 658–668.Google ScholarDigital Library
4. Marco Attene. 2017. ImatiSTL – Fast and Reliable Mesh Processing with a Hybrid Kernel. LNCS Transactions on Computational Science XXIX (2017), 86–96.Google Scholar
5. Marco Attene. 2018. As-exact-as-possible repair of unprintable STL files. Rapid Prototyping Journal (2018).Google Scholar
6. Marco Attene. 2020. Indirect predicates for Geometric Constructions. Computer-Aided Design (2020). Google ScholarCross Ref
7. Marco Attene, Marcel Campen, and Leif Kobbelt. 2013. Polygon mesh repairing: An application perspective. ACM Computing Surveys (CSUR) 45, 2 (2013), 15.Google ScholarDigital Library
8. Hichem Barki, Gael Guennebaud, and Sebti Foufou. 2015. Exact, robust, and efficient regularized Booleans on general 3D meshes. Computers & Mathematics with Applications 70, 6 (2015), 1235–1254.Google ScholarDigital Library
9. Gilbert Bernstein and Don Fussell. 2009. Fast, Exact, Linear Booleans. In Proceedings of the Symposium on Geometry Processing (SGP ’09). Eurographics Association, AirelaVille, Switzerland, Switzerland, 1269–1278. http://dl.acm.org/citation.cfm?id=1735603.1735606Google Scholar
10. Stephan Bischoff and Leif Kobbelt. 2005. Structure Preserving CAD Model Repair. Computer Graphics Forum 24, 3 (2005), 527–536. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1467-8659.2005.00878.x Google ScholarCross Ref
11. Hervé Brönnimann, Christoph Burnikel, and Sylvain Pion. 1998. Interval Arithmetic Yields Efficient Dynamic Filters for Computational Geometry. In Proceedings of the Fourteenth Annual Symposium on Computational Geometry (SCG ’98). ACM, New York, NY, USA, 165–174. Google ScholarDigital Library
12. Marcel Campen and Leif Kobbelt. 2010a. Exact and Robust (Self-)Intersections for Polygonal Meshes. Computer Graphics Forum 29, 2 (2010), 397–406. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1467-8659.2009.01609.x Google ScholarCross Ref
13. Marcel Campen and Leif Kobbelt. 2010b. Polygonal Boundary Evaluation of Minkowski Sums and Swept Volumes. Computer Graphics Forum 29, 5 (2010), 1613–1622. arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1467-8659.2010.01770.x Google ScholarCross Ref
14. Salles Viana Gomes de Magalhães, W Randolph Franklin, and Marcus Vinícius Alvim Andrade. 2020. An Efficient and Exact Parallel Algorithm for Intersecting Large 3-D Triangular Meshes Using Arithmetic Filters. Computer-Aided Design 120 (2020), 102801.Google ScholarDigital Library
15. Olivier Devillers, Sylvain Lazard, and William J. Lenhart. 2018. 3D Snap Rounding. In 34th International Symposium on Computational Geometry (SoCG 2018) (Leibniz International Proceedings in Informatics (LIPIcs)), Bettina Speckmann and Csaba D. Tóth (Eds.), Vol. 99. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, 30:1–30:14. Google ScholarCross Ref
16. Olivier Devillers and Sylvain Pion. 2003. Efficient exact geometric predicates for Delaunay triangulations. In Procs. of 5th Workshop Algorithm Eng. Exper. 37–44.Google Scholar
17. Steven Fortune and Christopher J. Van Wyk. 1993. Efficient Exact Arithmetic for Computational Geometry. In Proceedings of the Ninth Annual Symposium on Computational Geometry (SCG ’93). ACM, New York, NY, USA, 163–172. Google ScholarDigital Library
18. Laurent Fousse, Guillaume Hanrot, Vincent Lefèvre, Patrick Pélissier, and Paul Zimmermann. 2007. MPFR: A Multiple-precision Binary Floating-point Library with Correct Rounding. ACM Trans. Math. Softw. 33, 2, Article 13 (June 2007). Google ScholarDigital Library
19. Akash Garg, Alec Jacobson, and Eitan Grinspun. 2016. Computational design of reconfigurables. ACM Trans. Graph. 35, 4 (2016), 90–1.Google ScholarDigital Library
20. Philippe Guigue and Olivier Devillers. 2003. Fast and robust triangle-triangle overlap test using orientation predicates. Journal of graphics tools 8, 1 (2003), 25–32.Google ScholarCross Ref
21. Peter Hachenberger. 2009. Exact Minkowksi Sums of Polyhedra and Exact and Efficient Decomposition of Polyhedra into Convex Pieces. Algorithmica 55, 2 (01 Oct 2009), 329–345. Google ScholarDigital Library
22. Yixin Hu, Teseo Schneider, Bolun Wang, Denis Zorin, and Daniele Panozzo. 2019. Fast Tetrahedral Meshing in the Wild. arXiv preprint arXiv:1908.03581 (2019).Google Scholar
23. Yixin Hu, Qingnan Zhou, Xifeng Gao, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2018. Tetrahedral meshing in the wild. ACM Trans. Graph. 37, 4 (2018), 60–1.Google ScholarDigital Library
24. Alec Jacobson, Ladislav Kavan, and Olga Sorkine-Hornung. 2013. Robust inside-outside segmentation using generalized winding numbers. ACM Transactions on Graphics (TOG) 32, 4 (2013), 1–12.Google ScholarDigital Library
25. Wonhyung Jung, Hayong Shin, and Byoung Kyu Choi. 2003. Self-intersection Removal in Triangular Mesh Offsetting.Google Scholar
26. Bruno Lévy. 2016. Robustness and efficiency of geometric programs: The Predicate Construction Kit (PCK). Computer-Aided Design 72 (2016), 3–12.Google ScholarDigital Library
27. C. Li, S. Pion, and C.K. Yap. 2005. Recent progress in exact geometric computation. The Journal of Logic and Algebraic Programming 64, 1 (2005), 85 — 111. Practical development of exact real number computation. Google ScholarCross Ref
28. Marco Livesu. 2019. cinolib: a generic programming header only C++ library for processing polygonal and polyhedral meshes. Transactions on Computational Science XXXIV (2019). https://github.com/mlivesu/cinolib/. Google ScholarDigital Library
29. Andreas Meyer and Sylvain Pion. 2008. FPG: A code generator for fast and certified geometric predicates. In Real Numbers and Computers. 47–60.Google Scholar
30. Victor Milenkovic and Elisha Sacks. 2019. Geometric rounding and feature separation in meshes. Computer-Aided Design 108 (2019), 12–18.Google ScholarDigital Library
31. Alessandro Muntoni, Marco Livesu, Riccardo Scateni, Alla Sheffer, and Daniele Panozzo. 2018. Axis-aligned height-field block decomposition of 3d shapes. ACM Transactions on Graphics (TOG) 37, 5 (2018), 1–15.Google ScholarDigital Library
32. Daniele Panozzo and Alec Jacobson. 2014. LIBIGL: A C++ library for geometry processing without a mesh data structure. SGP 2014 Graduate School.Google Scholar
33. Sylvain Pion and Andreas Fabri. 2011. A generic lazy evaluation scheme for exact geometric computations. Science of Computer Programming 76, 4 (2011), 307 — 323. Special issue on library-centric software design (LCSD 2006). Google ScholarDigital Library
34. Rohan Sawhney and Keenan Crane. 2020. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 39, 4, Article 123 (July 2020), 18 pages. Google ScholarDigital Library
35. Silvia Sellán, Herng Yi Cheng, Yuming Ma, Mitchell Dembowski, and Alec Jacobson. 2019. Solid Geometry Processing on Deconstructed Domains. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 564–579.Google Scholar
36. Jonathan Richard Shewchuk. 1997. Adaptive precision floating-point arithmetic and fast robust geometric predicates. Discrete & Computational Geometry 18, 3 (1997), 305–363.Google ScholarCross Ref
37. Jonathan Richard Shewchuk and Brielin C Brown. 2015. Fast segment insertion and incremental construction of constrained Delaunay triangulations. Computational Geometry 48, 8 (2015), 554–574.Google ScholarDigital Library
38. Hang Si. 2015. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Transactions on Mathematical Software (TOMS) 41, 2 (2015), 1–36.Google ScholarDigital Library
39. K. Sugihara and M. Iri. 1990. A Solid Modelling System Free from Topological Inconsistency. J. Inf. Process. 12, 4 (April 1990), 380–393. Google ScholarDigital Library
40. The CGAL Project. 2019. CGAL User and Reference Manual (4.14.1 ed.). CGAL Editorial Board. https://doc.cgal.org/4.14.1/Manual/packages.htmlGoogle Scholar
41. Bolun Wang, Teseo Schneider, Yixin Hu, Marco Attene, and Daniele Panozzo. 2020. Exact and Efficient Polyhedral Envelope Containment Check. ACM Trans. Graph. 39, 4, Article 114 (July 2020), 14 pages. Google ScholarDigital Library
42. Jiaxian Yao, Danny M Kaufman, Yotam Gingold, and Maneesh Agrawala. 2017. Interactive design and stability analysis of decorative joinery for furniture. ACM Transactions on Graphics (TOG) 36, 2 (2017), 1–16.Google ScholarDigital Library
43. Qingnan Zhou, Eitan Grinspun, Denis Zorin, and Alec Jacobson. 2016. Mesh arrangements for solid geometry. ACM Transactions on Graphics (TOG) 35, 4 (2016), 39.Google ScholarDigital Library
44. Qingnan Zhou and Alec Jacobson. 2016. Thingi10k: A dataset of 10,000 3d-printing models. arXiv preprint arXiv:1605.04797 (2016).Google Scholar