“Connectivity editing for quadrilateral meshes”
Conference:
Type(s):
Title:
- Connectivity editing for quadrilateral meshes
Session/Category Title:
- Quads and Friends
Presenter(s)/Author(s):
Abstract:
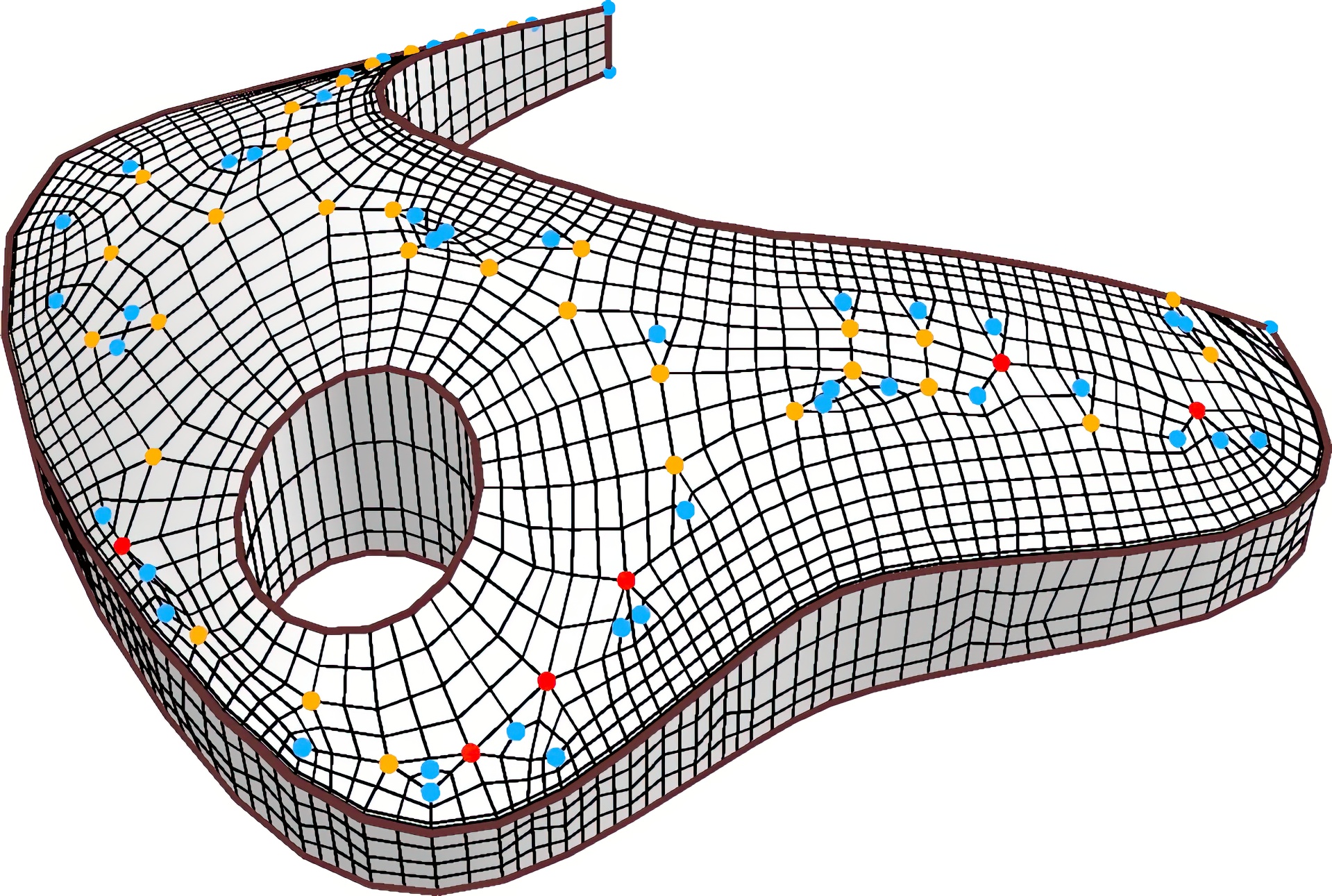
We propose new connectivity editing operations for quadrilateral meshes with the unique ability to explicitly control the location, orientation, type, and number of the irregular vertices (valence not equal to four) in the mesh while preserving sharp edges. We provide theoretical analysis on what editing operations are possible and impossible and introduce three fundamental operations to move and re-orient a pair of irregular vertices. We argue that our editing operations are fundamental, because they only change the quad mesh in the smallest possible region and involve the fewest irregular vertices (i.e., two). The irregular vertex movement operations are supplemented by operations for the splitting, merging, canceling, and aligning of irregular vertices. We explain how the proposed high-level operations are realized through graph-level editing operations such as quad collapses, edge flips, and edge splits. The utility of these mesh editing operations are demonstrated by improving the connectivity of quad meshes generated from state-of-art quadrangulation techniques.
References:
1. Akleman, E., and Chen, J. 2006. Practical polygonal mesh modeling with discrete gaussian-bonnet theorem. In GMP, 287–298.Google Scholar
2. Alliez, P., Meyer, M., and Desbrun, M. 2002. Interactive geometry remeshing. ACM Trans. Graph. 21, 3, 347–354. Google ScholarDigital Library
3. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. ACM Trans. Graph., 485–493. Google ScholarDigital Library
4. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3, 77. Google ScholarDigital Library
5. Bommes, D., Lempfer, T., and Kobbelt, L. 2011. Global structure optimization of quadrilateral meshes. In Computer Graphics Forum (Eurographics 2011), 375–384.Google Scholar
6. Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., and Levý, B. 2010. Polygon Mesh Processing. A K Peters, Natick, Massachusetts.Google Scholar
7. Daniels, J., Silva, C. T., Shepherd, J., and Cohen, E. 2008. Quadrilateral mesh simplification. ACM Trans. Graph., 148:1–148:9. Google ScholarDigital Library
8. Desbrun, M., Meyer, M., Schröder, P., and Barr, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In SIGGRAPH 1999, 317–324. Google ScholarDigital Library
9. Dong, S., Kircher, S., and Garland, M. 2005. Harmonic functions for quadrilateral remeshing of arbitrary manifolds. Comput. Aided Geom. Des. 22, 392–423. Google ScholarDigital Library
10. Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and Hart, J. C. 2006. Spectral surface quadrangulation. ACM Trans. Graph., 1057–1066. Google ScholarDigital Library
11. Hoppe, H. 1996. Progressive meshes. In SIGGRAPH 1996, 99–108. Google ScholarDigital Library
12. Hull, D., and Bacon, D. 2001. Introduction to dislocations. Butterworth-Heinemann.Google Scholar
13. Kälberer, F., Nieser, M., and Polthier, K. 2007. Quadcover – surface parameterization using branched coverings. Comput. Graph. Forum 26, 3, 375–384.Google ScholarCross Ref
14. Li, Y., Zhang, E., Kobayashi, Y., and Wonka, P. 2010. Editing operations for irregular vertices in triangle meshes. ACM Trans. Graph., 153:1–153:12. Google ScholarDigital Library
15. Marinov, M., and Kobbelt, L. 2004. Direct anisotropic quaddominant remeshing. In PG, 207–216. Google ScholarDigital Library
16. Myles, A., Pietroni, N., Kovacs, D., and Zorin, D. 2010. Feature-aligned t-meshes. ACM Trans. Graph., 117:1–117:11. Google ScholarDigital Library
17. Nasri, A., S. M., and Yasseen, Z. 2009. Filling n-sided regions by quad meshes for subdivision surfaces. vol. 28, 1644–1658.Google Scholar
18. Nieser, M., Palacios, J., Polthier, K., and Zhang, E. 2010. Hexagonal global parameterization of arbitrary surfaces. In ACM SIGGRAPH ASIA 2010 Sketches, ACM, New York, NY, USA, SA ’10, 5:1–5:2. Google ScholarDigital Library
19. Palacios, J., and Zhang, E. 2007. Rotational symmetry field design on surfaces. ACM Trans. Graph., 55. Google ScholarDigital Library
20. Ray, N., Li, W. C., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Trans. Graph. 25, 4, 1460–1485. Google ScholarDigital Library
21. Ray, N., Vallet, B., Li, W. C., and Lévy, B. 2008. Nsymmetry direction field design. ACM Trans. Graph. 27, 2, 10:1–10:13. Google ScholarDigital Library
22. Ray, N., Vallet, B., Alonso, L., and Lévy, B. 2009. Geometry aware direction field design. ACM Trans. Graph.. Google ScholarDigital Library
23. Schaefer, S., Warren, J., and Zorin, D., 2004. Lofting curve networks using subdivision surfaces.Google Scholar
24. Surazhsky, V., and Gotsman, C. 2003. Explicit surface remeshing. In 2003 Eurographics/ACM SIGGRAPH symposium on Geometry processing, 30. Google ScholarDigital Library
25. Tarini, M., Pietroni, N., Cignoni, P., Panozzo, D., and Puppo, E. 2010. Practical quad mesh simplification. vol. 29, 407–418.Google Scholar
26. Taubin, G. 2002. Detecting and reconstructing subdivision connectivity. The Visual Computer 18, 5–6.Google ScholarCross Ref
27. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. In SGP ’06, 201–210. Google ScholarDigital Library
28. Zhang, E., Mischaikow, K., and Turk, G. 2006. Vector field design on surfaces. ACM Trans. Graph. 25 (October), 1294–1326. Google ScholarDigital Library
29. Zhang, E., Hays, J., and Turk, G. 2007. Interactive tensor field design and visualization on surfaces. IEEE Transactions on Visualization and Computer Graphics 13, 1, 94–107. Google ScholarDigital Library
30. Zhang, M., Huang, J., Liu, X., and Bao, H. 2010. A wave-based anisotropic quadrangulation method. ACM Trans. Graph., 118:1–118:8. Google ScholarDigital Library