“Approximating subdivision surfaces with Gregory patches for hardware tessellation”
Conference:
Type(s):
Title:
- Approximating subdivision surfaces with Gregory patches for hardware tessellation
Session/Category Title:
- Geometry: interaction & subdivision
Presenter(s)/Author(s):
Moderator(s):
Abstract:
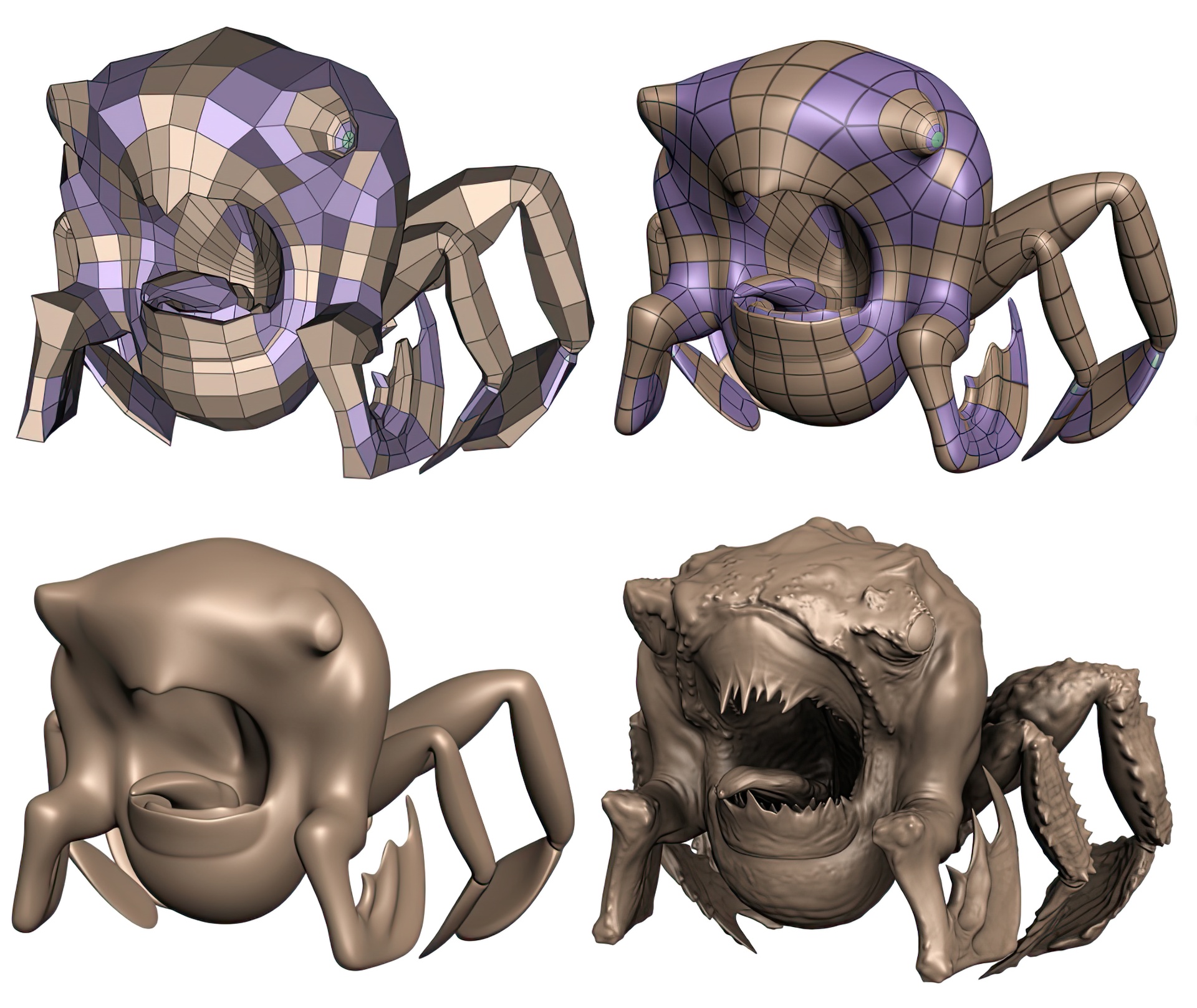
We present a new method for approximating subdivision surfaces with hardware accelerated parametric patches. Our method improves the memory bandwidth requirements for patch control points, translating into superior performance compared to existing methods. Our input is general, allowing for meshes that contain both quadrilateral and triangular faces in the input control mesh, as well as control meshes with boundary. We present two implementations of our scheme designed to run on Direct3D 11 class hardware equipped with a tessellator unit.
References:
1. Biermann, H., Levin, A., and Zorin, D. 2000. Piecewise smooth subdivision surfaces with normal control. In proceedings of SIGGRAPH, 113–120. Google ScholarDigital Library
2. Bolz, J., and Schröder, P. 2002. Rapid evaluation of catmull-clark subdivision surfaces. In Proceeding of the International Conference on 3D Web Technology, 11–17. Google ScholarDigital Library
3. Boubekeur, T., and Alexa, M. 2008. Phong tessellation. ACM Trans. Graph. 27, 5, 1–5. Google ScholarDigital Library
4. Boubekeur, T., and Schlick, C. 2007. Generic adaptive mesh refinement. In GPU Gems 3. Addison-Wesley, 93–104.Google Scholar
5. Boyd, C., 2008. Direct3D 11 Compute Shader. http://www.microsoft.com/downloads/details.aspx? FamilyId=9F943B2B-53EA-4F80-84B2-F05A360BFC6A.Google Scholar
6. Catmull, E., and Clark, J. 1978. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design 10, 6, 350–355.Google ScholarCross Ref
7. Chiyokura, H., and Kimura, F. 1983. Design of solids with free-form surfaces. Computer Graphics 17, 3, 289–298. Google ScholarDigital Library
8. Cignoni, P., Rocchini, C., and Scopigno, R. 1998. Metro: Measuring error on simplified surfaces. Computer Graphics Forum 17, 2, 167–174.Google Scholar
9. Drone, S., Lee, M., and Oneppo, M., 2008. Direct3D 11 Tessellation. http://www.microsoft.com/downloads/details.aspx? FamilyId=2D5BC492-0E5C-4317-8170-E952DCA10D46.Google Scholar
10. Forsyth, T., 2006. Linear-speed vertex cache optimisation. http://home.comcast.net/tom_forsyth/papers/fast_vert_cache_opt.html.Google Scholar
11. Gregory, J. 1974. Smooth interpolation without twist constraints. In Computer Aided Geometric Design, R. E. Barnhill and R. F. Riesenfeld, Eds. Acadmic Press, New York, 71–87.Google Scholar
12. Halstead, M., Kass, M., and DeRose, T. 1993. Efficient, fair interpolation using catmull-clark surfaces. In Proceedings of SIGGRAPH, 35–44. Google ScholarDigital Library
13. Kovacs, D., Mitchell, J., Drone, S., and Zorin, D. 2009. Real-time creased approximate subdivision surfaces. In Proceedings of the symposium on Interactive 3D graphics, 155–160. Google ScholarDigital Library
14. Lee, A., Moreton, H., and Hoppe, H. 2000. Displaced subdivision surfaces. In Proceedings of SIGGRAPH, 85–94. Google ScholarDigital Library
15. Lin, G., and Yu, T. P. Y. 2006. An improved vertex caching scheme for 3d mesh rendering. IEEE Transactions on Visualization and Computer Graphics 12, 4, 640–648. Google ScholarDigital Library
16. Longhi, L. 1987. Interpolating patches between cubic boundaries. Tech. Rep. CSD-87-313, University of California. Google ScholarDigital Library
17. Loop, C., and Schaefer, S. 2008. Approximating catmull-clark subdivision surfaces with bicubic patches. ACM Trans. Graph. 27, 1, 8:1–8:11. Google ScholarDigital Library
18. Myles, A., Ni, T., and Peters, J. 2008. Fast parallel construction of smooth surfaces from meshes with tri/quad/pent facets. Computer Graphics Forum 27, 5, 1365–1372.Google ScholarDigital Library
19. Myles, A., Yeo, Y. I., and Peters, J. 2008. Gpu conversion of quad meshes to smooth surfaces. In SPM ’08: ACM symposium on Solid and physical modeling, 321–326. Google ScholarDigital Library
20. Ni, T., Yeo, Y. I., Myles, A., Goel, V., and Peters, J. 2008. Gpu smoothing of quad meshes. In SMI ’08: IEEE International Conference on Shape Modeling and Applications, 3–9.Google Scholar
21. Peters, J. 2000. Patching catmull-clark meshes. In Proceedings of SIGGRAPH, 255–258. Google ScholarDigital Library
22. Sander, P. V., Nehab, D., and Barczak, J. 2007. Fast triangle reordering for vertex locality and reduced overdraw. ACM Trans. Graph. 26, 3, 89. Google ScholarDigital Library
23. Shiue, L.-J., Jones, I., and Peters, J. 2005. A real-time gpu subdivision kernel. ACM Trans. Graph. 24, 3, 1010–1015. Google ScholarDigital Library
24. Stam, J., and Loop, C. 2003. Quad/triangle subdivision. Computer Graphics Forum 22, 1, 1–7.Google ScholarCross Ref
25. Stam, J. 1998. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. Computer Graphics 32, Annual Conference Series, 395–404. Google ScholarDigital Library
26. Vlachos, A., Peters, J., Boyd, C., and Mitchell, J. L. 2001. Curved pn triangles. In Proceedings of the Symposium on Interactive 3D Graphics, 159–166. Google ScholarDigital Library