“Approximate dissections” by Duncan, Yu, Yeung and Terzopoulos
Conference:
Type(s):
Title:
- Approximate dissections
Session/Category Title:
- Geometry and Shape
Presenter(s)/Author(s):
Abstract:
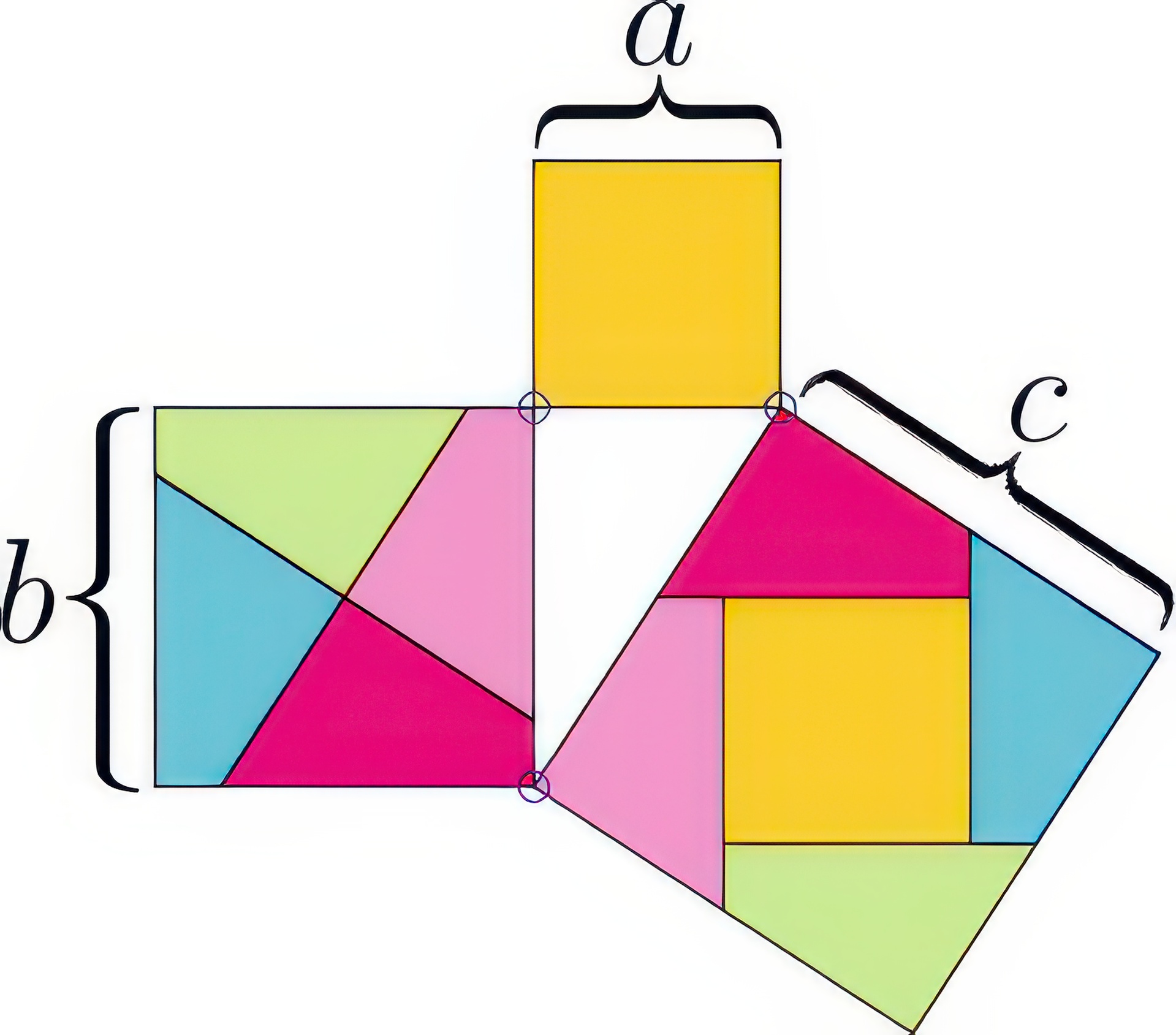
A geometric dissection is a set of pieces which can be assembled in different ways to form distinct shapes. Dissections are used as recreational puzzles because it is striking when a single set of pieces can construct highly different forms. Existing techniques for creating dissections find pieces that reconstruct two input shapes exactly. Unfortunately, these methods only support simple, abstract shapes because an excessive number of pieces may be needed to reconstruct more complex, naturalistic shapes. We introduce a dissection design technique that supports such shapes by requiring that the pieces reconstruct the shapes only approximately. We find that, in most cases, a small number of pieces suffices to tightly approximate the input shapes. We frame the search for a viable dissection as a combinatorial optimization problem, where the goal is to search for the best approximation to the input shapes using a given number of pieces. We find a lower bound on the tightness of the approximation for a partial dissection solution, which allows us to prune the search space and makes the problem tractable. We demonstrate our approach on several challenging examples, showing that it can create dissections between shapes of significantly greater complexity than those supported by previous techniques.
References:
1. J. Bosboom, E.D. Demaine, M.L. Demaine, J. Lynch, P. Manurangsi, M. Rudoy, and A. Yodpinyanee. 2015. k-Piece dissection is NP-hard. In Abstracts from the 18th Japan Conf. on Discrete and Computational Geometry and Graphs. 2.
2. M.J. Cohn. 1975. Economical triangle-square dissection. Geometriae Dedicata 3, 4 (1975), 447–467. Cross Ref
3. G.N. Frederickson. 2002. Hinged Dissections: Swinging and Twisting. Cambridge University Press.
4. G.N. Frederickson. 2003. Dissections: Plane and Fancy. Cambridge University Press.
5. R.J. Gardner. 1985. A problem of Sallee on equidecomposable convex bodies. Proc. American Mathematical Society 94, 2 (1985), 329–332. Cross Ref
6. Gurobi Optimization, Inc. 2016. Gurobi Optimizer Reference Manual. (2016). http://www.gurobi.com
7. Y.-J. Huang, S.-Y. Chan, W.-C. Lin, and S.-Y. Chuang. 2016. Making and animating transformable 3D models. Computers & Graphics 54 (2016), 127–134.
8. C.S. Kaplan and D.H. Salesin. 2000. Escherization. In Proc. ACM SIGGRAPH ’00 Conf. 499–510.
9. E. Kranakis, D. Krizanc, and J. Urrutia. 2000. Efficient regular polygon dissections. Geometriae Dedicata 80, 1 (2000), 247–262. Cross Ref
10. K.C. Kwan, L.T. Sinn, C. Han, T.-T. Wong, and C.-W. Fu. 2016. Pyramid of arclength descriptor for generating collage of shapes. ACM Transactions on Graphics (TOG) 35, 6 (2016), 229.
11. M. Löffler, M. Kaiser, T. van Kapel, G. Klappe, M. van Kreveld, and F. Staals. 2014. The Connect-The-Dots family of puzzles: Design and automatic generation. ACM Transactions on Graphics (TOG) 33, 4 (2014), 72.
12. P. Manurangsi, M. Rudoy, and A. Yodpinyanee. 2016. Dissection with the fewest pieces is hard, even to approximate. In Discrete and Computational Geometry and Graphs: 18th Japan Conf. (JCDCGG 2015), Vol. 9943. 37.
13. P. Song, C.-W. Fu, Y. Jin, H. Xu, L. Liu, P.-A. Heng, and D. Cohen-or. 2017. Reconfigurable interlocking furniture. ACM Transactions on Graphics (TOG) 36, 6, Article 174 (2017), 14 pages.
14. A. Wächter and L.T. Biegler. 2006. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical programming 106, 1 (2006), 25–57.
15. J. Xu and C.S. Kaplan. 2007. Image-guided maze construction. ACM Transactions on Graphics (TOG) 26, 3, Article 29 (2007), 9 pages.
16. X. Xu, L. Zhang, and T.-T. Wong. 2010. Structure-based ASCII art. ACM Transactions on Graphics (TOG) 29, 4, Article 52 (2010), 9 pages.
17. Y. Zhou, S. Sueda, W. Matusik, and A. Shamir. 2014. Boxelization: Folding 3D objects into boxes. ACM Transactions on Graphics (TOG) 33, 4 (2014), 71.
18. Y. Zhou, R. Wang, et al. 2012. An algorithm for creating geometric dissection puzzles. In Proc. Bridges Conf. 49–58.
19. C. Zou, J. Cao, W. Ranaweera, I. Alhashim, P. Tan, A. Sheffer, and H. Zhang. 2016. Legible compact calligrams. ACM Transactions on Graphics (TOG) 35, 4 (2016), 122.