“A Differential Monte Carlo Solver for the Poisson Equation”
Conference:
Type(s):
Title:
- A Differential Monte Carlo Solver for the Poisson Equation
Presenter(s)/Author(s):
Abstract:
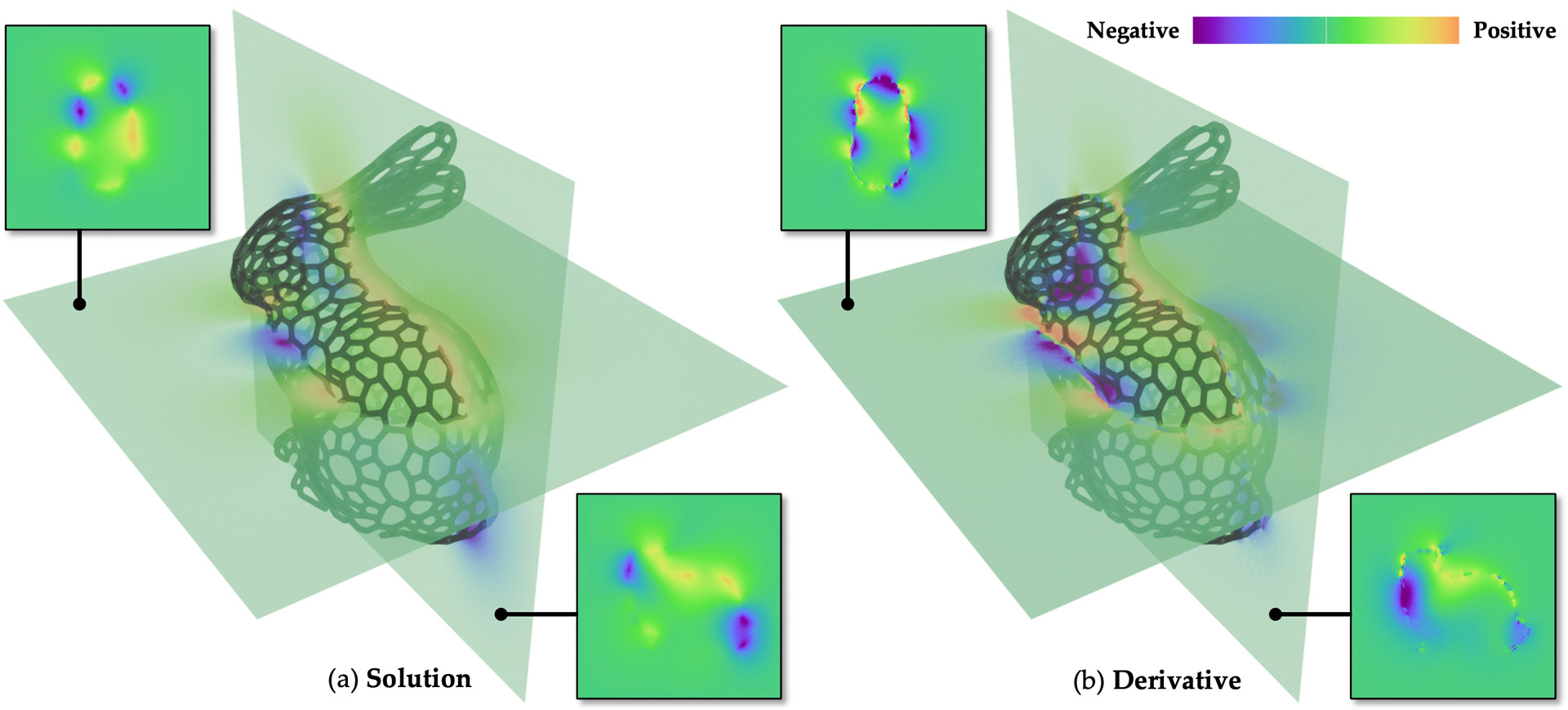
We introduce a general technique that differentiates solutions to the Poisson equation with Dirichlet boundary conditions. Specifically, we devise a new boundary-integral formulation for the derivatives with respect to arbitrary parameters including shapes of the domain. Further, we develop an efficient walk-on-spheres technique based on our new formulation.
References:
[1]
Ilia Binder and Mark Braverman. 2012. The rate of convergence of the walk on spheres algorithm. Geometric and Functional Analysis 22, 3 (2012), 558?587.
[2]
J.M Delaurentis and L.A Romero. 1990. A Monte Carlo method for Poisson?s equation. J. Comput. Phys. 90, 1 (1990), 123?140.
[3]
Michel Delfour and Jean-Paul Zolsio. 2010. Shapes and Geometries: Metrics, Analysis, Differential Calculus, and Optimization. Society for Industrial and Applied Mathematics.
[4]
L.C. Evans. 2010. Partial Differential Equations. American Mathematical Society.
[5]
Jaroslav Haslinger and Raino AE M?kinen. 2003. Introduction to shape optimization: theory, approximation, and computation. SIAM.
[6]
Dan Henry. 2005. Perturbation of the boundary in boundary-value problems of partial differential equations. Number 318. Cambridge University Press.
[7]
Wenzel Jakob, S?bastien Speierer, Nicolas Roussel, and Delio Vicini. 2022. DR.JIT: a just-in-time compiler for differentiable rendering. ACM Trans. Graph. 41, 4 (2022), 124:1?124:19.
[8]
Shizuo Kakutani. 1944. 143. Two-dimensional Brownian Motion and Harmonic Functions. Proceedings of the Imperial Academy 20, 10 (1944), 706?714.
[9]
Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
[10]
Bailey Miller, Rohan Sawhney, Keenan Crane, and Ioannis Gkioulekas. 2023. Boundary Value Caching for Walk on Spheres. ACM Trans. Graph. 42, 4 (2023), 82:1?82:11.
[11]
Mervin E. Muller. 1956. Some Continuous Monte Carlo Methods for the Dirichlet Problem. The Annals of Mathematical Statistics 27, 3 (1956), 569 ? 589.
[12]
Alexandrina Orzan, Adrien Bousseau, Holger Winnem?ller, Pascal Barla, Jo?lle Thollot, and David Salesin. 2008. Diffusion curves: a vector representation for smooth-shaded images. ACM Trans. Graph. 27, 3 (2008), 1?8.
[13]
Yang Qi, Dario Seyb, Benedikt Bitterli, and Wojciech Jarosz. 2022. A bidirectional formulation for Walk on Spheres. Computer Graphics Forum 41, 4 (2022), 51?62.
[14]
O. Reynolds. 1903. Papers on mechanical and physical subjects: the sub-mechanics of the universe. Vol. 3. The University Press.
[15]
Karl Karlovich Sabelfeld. 1982. Vector algorithms in the Monte-Carlo method for solving systems of second-order elliptic equations and Lame?s equation. In Doklady Akademii Nauk, Vol. 262. Russian Academy of Sciences, 1076?1080.
[16]
Rohan Sawhney and Keenan Crane. 2020. Monte Carlo geometry processing: a grid-free approach to PDE-based methods on volumetric domains. ACM Trans. Graph. 39, 4 (2020), 123:1?123:18.
[17]
Rohan Sawhney, Bailey Miller, Ioannis Gkioulekas, and Keenan Crane. 2023. Walk on Stars: A Grid-Free Monte Carlo Method for PDEs with Neumann Boundary Conditions. ACM Trans. Graph. 42, 4 (2023), 80:1?80:20.
[18]
Rohan Sawhney, Dario Seyb, Wojciech Jarosz, and Keenan Crane. 2022. Grid-Free Monte Carlo for PDEs with Spatially Varying Coefficients. ACM Trans. Graph. 41, 4 (2022), 53:1?53:17.
[19]
Jan Sokolowski and Jean-Paul Zol?sio. 1992. Introduction to shape optimization. Springer.
[20]
Ryusuke Sugimoto, Terry Chen, Yiti Jiang, Christopher Batty, and Toshiya Hachisuka. 2023. A Practical Walk-on-Boundary Method for Boundary Value Problems. ACM Trans. Graph. 42, 4 (2023), 81:1?81:16.
[21]
Shawn Walker. 2015. The Shapes of Things: A Practical Guide to Differential Geometry and the Shape Derivative. Society for Industrial and Applied Mathematics.
[22]
Ekrem Fatih Yilmazer, Delio Vicini, and Wenzel Jakob. 2022. Solving inverse PDE problems using grid-free Monte Carlo estimators. https://arxiv.org/abs/2208.02114
[23]
Shuang Zhao, Fr?do Durand, and Changxi Zheng. 2018. Inverse Diffusion Curves Using Shape Optimization. IEEE Transactions on Visualization and Computer Graphics 24, 7 (2018), 2153?2166.