“Metric Optimization in Penner Coordinates” by Capouellez and Zorin
Conference:
Type(s):
Title:
- Metric Optimization in Penner Coordinates
Session/Category Title: Embed to a Different Space
Presenter(s)/Author(s):
Abstract:
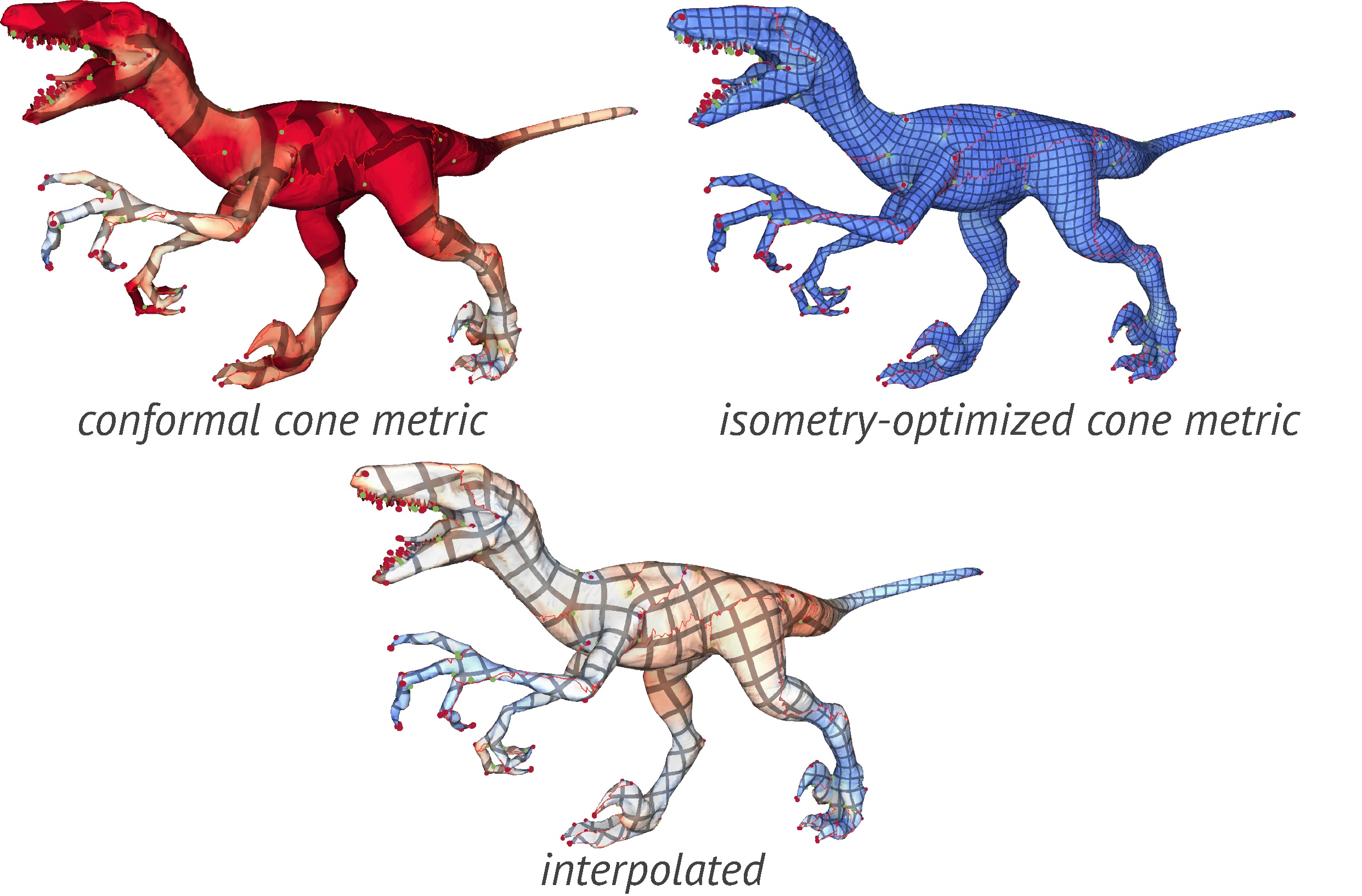
Many parametrization and mapping-related problems in geometry processing can be viewed as metric optimization problems, i.e., computing a metric minimizing a functional and satisfying a set of constraints, such as flatness. Penner coordinates are global coordinates on the space of metrics on meshes with a fixed vertex set and topology, but varying connectivity, making it homeomorphic to the Euclidean space of dimension equal to the number of edges in the mesh, without any additional constraints imposed, and reducing to logarithms of edge lengths when restricted to a fixed connectivity. These coordinates play an important role in the theory of discrete conformal maps, enabling recent development of highly robust algorithms with convergence and solution existence guarantees for computing such maps. We demonstrate how Penner coordinates can be used to solve a general class of problems involving metrics, including optimization and interpolation, while retaining the key guarantees available for conformal maps.