“Q-zip: singularity editing primitive for quad meshes” by Feng, Tong and Desbrun
Conference:
Type(s):
Title:
- Q-zip: singularity editing primitive for quad meshes
Session/Category Title: Meshing
Presenter(s)/Author(s):
Abstract:
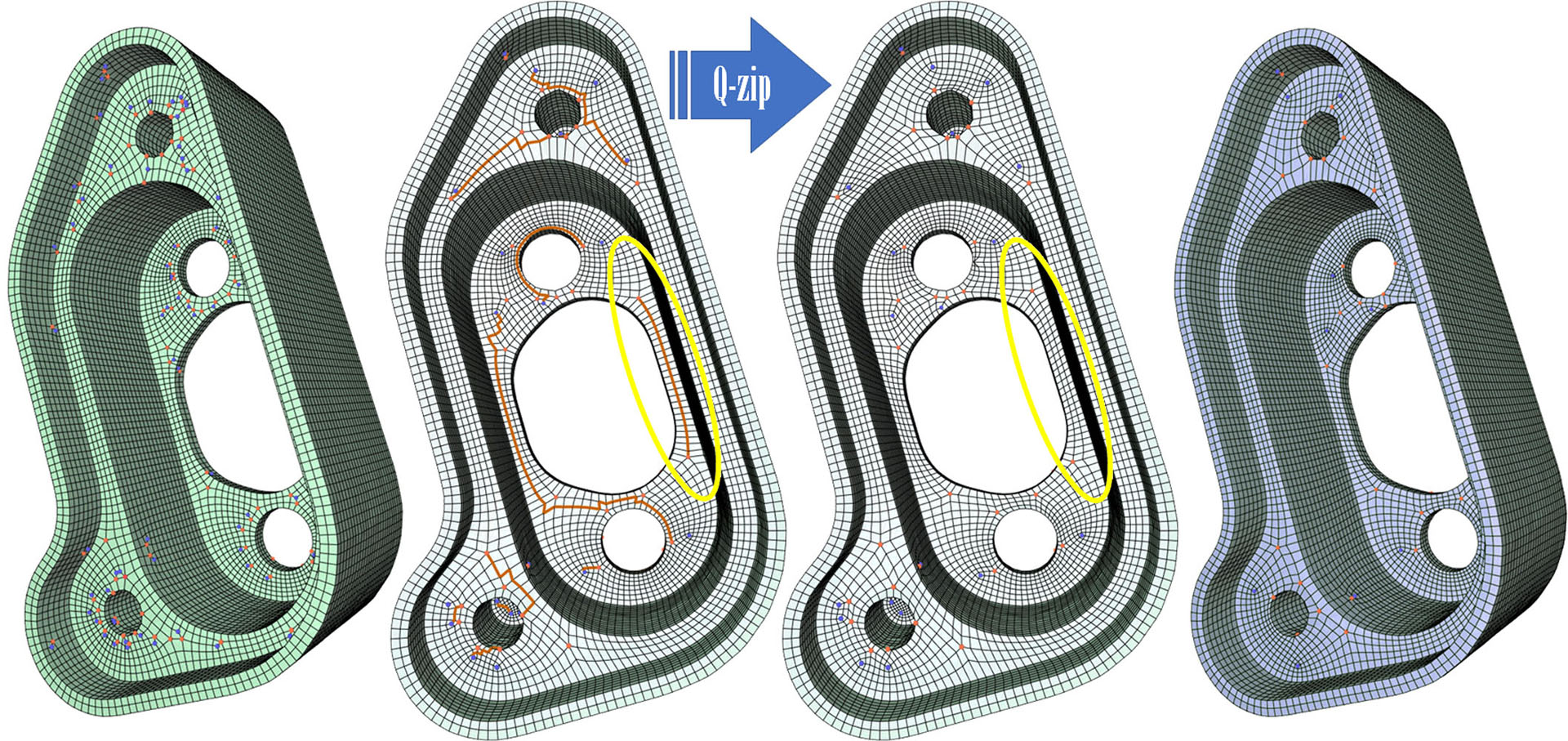
Singularity editing of a quadrangle mesh consists in shifting singularities around for either improving the quality of the mesh elements or canceling extraneous singularities, so as to increase mesh regularity. However, the particular structure of a quad mesh renders the exploration of allowable connectivity changes non-local and hard to automate. In this paper, we introduce a simple, principled, and general quad-mesh editing primitive with which pairs of arbitrarily distant singularities can be efficiently displaced around a mesh through a deterministic and reversible chain of local topological operations with a minimal footprint. Dubbed Q-zip as it acts as a zipper opening up and collapsing down quad strips, our practical mesh operator for singularity editing can be easily implemented via parallel transport of a reference compass between any two irregular vertices. Batches of Q-zips performed in parallel can then be used for efficient singularity editing.
References:
1. Ansys. 2020. Meshing User’s Guide. http://www.ansys.com ANSYS, 275 Technology Drive, Canonsburg, PA 15317.
2. David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, and Leif Kobbelt. 2013. Integer-grid Maps for Reliable Quad Meshing. ACM Trans. Graph. 32, 4, Article 98 (2013).
3. David Bommes, Timm Lempfer, and Leif Kobbelt. 2011. Global Structure Optimization of Quadrilateral Meshes. Computer Graphics Forum 30, 2 (2011), 375–384.
4. David Bommes, Bruno Lévy, Nico Pietroni, Enrico Puppo, Claudio Silva, Marco Tarini, and Denis Zorin. 2012. State of the Art in Quad Meshing. In Eurographics State-of-The-Art Reports.
5. David Bommes, Henrik Zimmer, and Leif Kobbelt. 2009. Mixed-integer Quadrangulation. ACM Trans. Graph. 28, 3, Article 77 (July 2009), 10 pages.
6. Edwin E. Catmull and James. H. Clark. 1978. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design 10, 6 (1978), 350–355.
7. Joel Daniels, Claudio T. Silva, and Elaine Cohen. 2009. Localized Quadrilateral Coarsening. Computer Graphics Forum 28, 5 (2009), 1437–1444.
8. Joel Daniels, Cláudio T. Silva, Jason Shepherd, and Elaine Cohen. 2008. Quadrilateral Mesh Simplification. ACM Trans. Graph. 27, 5, Article 148 (2008).
9. Julia Docampo-Sanchez and Robert Haimes. 2019. Towards Fully Regular Quad Mesh Generation.
10. Shen Dong, Peer-Timo Bremer, Michael Garland, Valerio Pascucci, and John C. Hart. 2006. Spectral Surface Quadrangulation. ACM Trans. Graph. 25, 3 (July 2006), 1057–1066.
11. Hans-Christian Ebke, Marcel Campen, David Bommes, and Leif Kobbelt. 2014. Level-of-Detail Quad Meshing. ACM Trans. Graph. 33, 6, Article 184 (2014).
12. Hans-Christian Ebke, Patrick Schmidt, Marcel Campen, and Leif Kobbelt. 2016. Interactively Controlled Quad Remeshing of High Resolution 3D Models. ACM Trans. Graph. 35, 6, Article 218 (2016).
13. Xianzhong Fang, Hujun Bao, Yiying Tong, Mathieu Desbrun, and Jin Huang. 2018. Quad-rangulation through Morse-Parameterization Hybridization. ACM Trans. Graph. 37, 4, Article 92 (2018).
14. Allen Hatcher. 2002. Algebraic Topology. Cambridge University Press.
15. Jingwei Huang, Yichao Zhou, Matthias Niessner, Jonathan Richard Shewchuk, and Leonidas J. Guibas. 2018. QuadriFlow: A Scalable and Robust Method for Quadrangulation. Computer Graphics Forum (2018).
16. Wenzel Jakob, Marco Tarini, Daniele Panozzo, and Olga Sorkine-Hornung. 2015. Instant Field-Aligned Meshes. ACM Transactions on Graphics 34, 6, Article 189 (2015).
17. Felix Kälberer, Matthias Nieser, and Konrad Polthier. 2007. QuadCover – Surface Parameterization using Branched Coverings. Computer Graphics Forum 26, 3 (2007), 375–384.
18. Yuanyuan Li, Eugene Zhang, Yoshihiro Kobayashi, and Peter Wonka. 2010. Editing Operations for Irregular Vertices in Triangle Meshes. ACM Trans. Graph. 29, 6, Article 153.
19. M. Lyon, D. Bommes, and L. Kobbelt. 2020. Cost Minimizing Local Anisotropic Quad Mesh Refinement. Computer Graphics Forum 39, 5 (2020), 163–172.
20. Ashish Myles and Denis Zorin. 2013. Controlled-Distortion Constrained Global Parametrization. ACM Trans. Graph. 32, 4, Article 105 (2013).
21. Steve J. Owen, Matthew L. Staten, Scott A. Canann, and Sunil Saigal. 1999. Q-Morph: an indirect approach to advancing front quad meshing. Int. J. Num. Meth. Eng. 44, 9 (1999), 1317–1340.
22. Chi-Han Peng, Eugene Zhang, Yoshihiro Kobayashi, and Peter Wonka. 2011. Connectivity Editing for Quadrilateral Meshes. ACM Trans. Graph. 30, 6, Article 141 (2011).
23. Nicolas Ray, Bruno Vallet, Laurent Alonso, and Bruno Levy. 2009. Geometry-Aware Direction Field Processing. ACM Trans. Graph. 29, 1, Article 1 (2009).
24. Ahmad A. Rushdi, Scott A. Mitchell, Ahmed H. Mahmoud, Chandrajit C. Bajaj, and Mohamed S. Ebeida. 2017. All-quad meshing without cleanup. Computer-Aided Design 85 (2017), 83–98.
25. Marco Tarini, Nico Pietroni, Paolo Cignoni, Daniele Panozzo, and Enrico Puppo. 2010. Practical quad mesh simplification. Computer Graphics Forum 29, 2 (2010), 407–418.
26. Marco Tarini, Enrico Puppo, Daniele Panozzo, Nico Pietroni, and Paolo Cignoni. 2011. Simple Quad Domains for Field Aligned Mesh Parametrization. ACM Transactions on Graphics (SIGGRAPH Asia) 30, 6 (2011).
27. Chaman Singh Verma and Krishnan Suresh. 2017. A Robust Combinatorial Approach to Reduce Singularities in Quadrilateral Meshes. Comput. Aided Des. 85, C (April 2017), 99–110.
28. Jianhua Wu and Leif Kobbelt. 2002. Fast Mesh Decimation by Multiple-Choice Techniques. In Workshop on Vision, Modeling, and Visualization. 241–248.
29. Kaoji Xu, Muhammad Naeem Akram, and Guoning Chen. 2020. Semi-Global Quad Mesh Structure Simplification via Separatrix Operations. In SIGGRAPH Asia 2020 Technical Communications. Article 2.
30. Xiaotian Yin, Miao Jin, and Xianfeng Gu. 2007. Computing shortest cycles using universal covering space. Visual Comput. 23, 12 (2007), 999–1004.
31. Muyang Zhang, Jin Huang, Xinguo Liu, and Hujun Bao. 2010. A Wave-Based Anisotropic Quadrangulation Method. In ACM SIGGRAPH Proceedings. Article 118.