“Generalized adaptive refinement for grid-based hexahedral meshing” by Pitzalis, Livesu, Cherchi, Gobbetti and Scateni
Conference:
Type(s):
Title:
- Generalized adaptive refinement for grid-based hexahedral meshing
Session/Category Title: Geometry Processing and Simulation
Presenter(s)/Author(s):
Abstract:
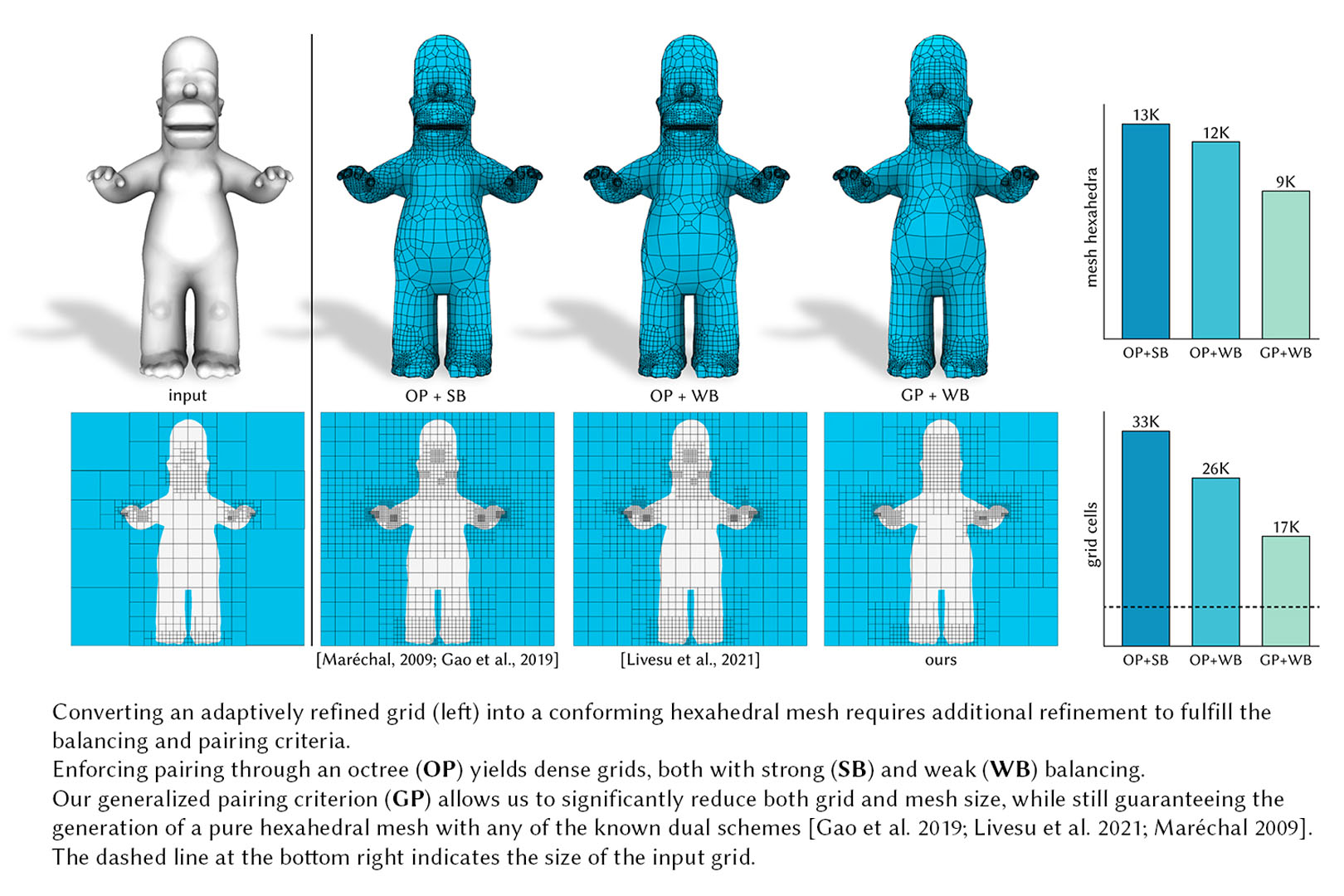
Due to their nice numerical properties, conforming hexahedral meshes are considered a prominent computational domain for simulation tasks. However, the automatic decomposition of a general 3D volume into a small number of hexahedral elements is very challenging. Methods that create an adaptive Cartesian grid and convert it into a conforming mesh offer superior robustness and are the only ones concretely used in the industry. Topological schemes that permit this conversion can be applied only if precise compatibility conditions among grid elements are observed. Some of these conditions are local, hence easy to formulate; others are not and are much harder to satisfy. State-of-the-art approaches fulfill these conditions by prescribing additional refinement based on special building rules for octrees. These methods operate in a restricted space of solutions and are prone to severely over-refine the input grids, creating a bottleneck in the simulation pipeline. In this article, we introduce a novel approach to transform a general adaptive grid into a new grid meeting hexmeshing criteria, without resorting to tree rules. Our key insight is that we can formulate all compatibility conditions as linear constraints in an integer programming problem by choosing the proper set of unknowns. Since we operate in a broader solution space, we are able to meet topological hexmeshing criteria at a much coarser scale than methods using octrees, also supporting generalized grids of any shape or topology. We demonstrate the superiority of our approach for both traditional grid-based hexmeshing and adaptive polycube-based hexmeshing. In all our experiments, our method never prescribed more refinement than the prior art and, in the average case, it introduced close to half the number of extra cells.
References:
1. Noam Aigerman and Yaron Lipman. 2013. Injective and bounded distortion mappings in 3D. ACM Transactions on Graphics (TOG) 32, 4 (2013), 1–14.
2. Cecil G Armstrong, Harold J Fogg, Christopher M Tierney, and Trevor T Robinson. 2015. Common themes in multi-block structured quad/hex mesh generation. Procedia Engineering 124 (2015), 70–82.
3. Arthur Bawin, François Henrotte, and Jean-François Remacle. 2020. Automatic feature-preserving size field for 3D mesh generation. arXiv:2009.03984 [math.NA]
4. Steven E Benzley, Ernest Perry, Karl Merkley, Brett Clark, and Greg Sjaardama. 1995. A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In Proceedings, 4th international meshing roundtable, Vol. 17. Citeseer, 179–191.
5. Ted Blacker. 2000. Meeting the challenge for automated conformal hexahedral meshing. In Proc. 9th international meshing roundtable. Springer, 11–20.
6. Matteo Bracci, Marco Tarini, Nico Pietroni, Marco Livesu, and Paolo Cignoni. 2019. HexaLab.net: an Online Viewer for Hexahedral Meshes. Computer-Aided Design 110 (2019), 24–36. https://www.hexalab.net/
7. Gianmarco Cherchi, Pierre Alliez, Riccardo Scateni, Max Lyon, and David Bommes. 2019. Selective Padding for Polycube-Based Hexahedral Meshing. Computer Graphics Forum 38, 1 (2019), 580–591.
8. Gianmarco Cherchi, Marco Livesu, and Riccardo Scateni. 2016. Polycube Simplification for Coarse Layouts of Surfaces and Volumes. Computer Graphics Forum 35, 5 (2016), 11–20.
9. AO Cifuentes and A Kalbag. 1992. A performance study of tetrahedral and hexahedral elements in 3-D finite element structural analysis. Finite Elements in Analysis and Design 12, 3-4 (1992), 313–318.
10. Etienne Corman and Keenan Crane. 2019. Symmetric moving frames. ACM Transactions on Graphics (TOG) 38, 4 (2019), 87:1–87:16.
11. Distene SAS. 2020. MeshGems. http://www.meshgems.com/volume-meshing-meshgems-hexa.html
12. Thomas Nelson Erke Wang and Rainer Rauch. 2004. Back to elements-tetrahedra vs. hexahedra. In Proc. International ANSYS conference.
13. Xianzhong Fang, Weiwei Xu, Hujun Bao, and Jin Huang. 2016. All-hex meshing using closed-form induced polycube. ACM Transactions on Graphics (TOG) 35, 4 (2016), 124:1–124:9.
14. Xiao-Ming Fu, Chong-Yang Bai, and Yang Liu. 2016. Efficient volumetric polycube-map construction. Computer Graphics Forum 35, 7 (2016), 97–106.
15. Xifeng Gao, Hanxiao Shen, and Daniele Panozzo. 2019. Feature Preserving Octree-Based Hexahedral Meshing. Computer Graphics Forum 38, 5 (2019), 135–149.
16. Vladimir Garanzha, Igor Kaporin, Liudmila Kudryavtseva, François Protais, Nicolas Ray, and Dmitry Sokolov. 2021. Foldover-free maps in 50 lines of code. arXiv preprint arXiv:2102.03069 (2021).
17. James Gregson, Alla Sheffer, and Eugene Zhang. 2011. All-hex mesh generation via volumetric polycube deformation. Computer Graphics Forum 30, 5 (2011), 1407–1416.
18. LLC Gurobi Optimization. 2020. Gurobi Optimizer Reference Manual. http://www.gurobi.com
19. Kangkang Hu, Jin Qian, and Yongjie Zhang. 2013. Adaptive all-hexahedral mesh generation based on a hybrid octree and bubble packing. In Proc. 22nd International Meshing Roundtable – Research Notes. Sandia National Laboratories, 5B3:1–5B3:5.
20. Kangkang Hu and Yongjie Jessica Zhang. 2016. Centroidal Voronoi tessellation based polycube construction for adaptive all-hexahedral mesh generation. Computer Methods in Applied Mechanics and Engineering 305 (2016), 405–421.
21. Jin Huang, Tengfei Jiang, Zeyun Shi, Yiying Tong, Hujun Bao, and Mathieu Desbrun. 2014. L1-based construction of polycube maps from complex shapes. ACM Transactions on Graphics (TOG) 33, 3 (2014), 25:1–25:11.
22. Yasushi Ito, Alan M Shih, and Bharat K Soni. 2009. Octree-based reasonable-quality hexahedral mesh generation using a new set of refinement templates. Internat. J. Numer. Methods Engrg. 77, 13 (2009), 1809–1833.
23. Tengfei Jiang, Jin Huang, Yuanzhen Wang, Yiying Tong, and Hujun Bao. 2013. Frame field singularity correctionfor automatic hexahedralization. IEEE Transactions on Visualization and Computer Graphics 20, 8 (2013), 1189–1199.
24. Michael Kremer, David Bommes, Isaak Lim, and Leif Kobbelt. 2014. Advanced automatic hexahedral mesh generation from surface quad meshes. In Proc. 22nd International Meshing Roundtable. Springer, 147–164.
25. Franck Ledoux and Jean-Christophe Weill. 2008. An extension of the reliable whisker weaving algorithm. In Proc. 16th International Meshing Roundtable. Springer, 215–232.
26. Yufei Li, Yang Liu, Weiwei Xu, Wenping Wang, and Baining Guo. 2012. All-hex meshing using singularity-restricted field. ACM Transactions on Graphics (TOG) 31, 6 (2012), 177:1–177:11.
27. Hongwei Lin, Sinan Jin, Hongwei Liao, and Qun Jian. 2015. Quality guaranteed all-hex mesh generation by a constrained volume iterative fitting algorithm. Computer-Aided Design 67 (2015), 107–117.
28. Heng Liu, Paul Zhang, Edward Chien, Justin Solomon, and David Bommes. 2018. Singularity-constrained octahedral fields for hexahedral meshing. ACM Transations on Graphics (TOG) 37, 4 (2018), 93:1–93:17.
29. Marco Livesu. 2019. Cinolib: A Generic Programming Header Only C++ Library for Processing Polygonal and Polyhedral Meshes. Transactions on Computational Science XXXIV 34 (2019), 64–76. https://github.com/mlivesu/cinolib/.
30. Marco Livesu, Alessandro Muntoni, Enrico Puppo, and Riccardo Scateni. 2016. Skeleton-driven adaptive hexahedral meshing of tubular shapes. Computer Graphics Forum 35, 7 (2016), 237–246.
31. Marco Livesu, Nico Pietroni, Enrico Puppo, Alla Sheffer, and Paolo Cignoni. 2020. LoopyCuts: practical feature-preserving block decomposition for strongly hex-dominant meshing. ACM Transactions on Graphics (TOG) 39, 4 (2020), 121:1–121:17.
32. Marco Livesu, Luca Pitzalis, and Gianmarco Cherchi. 2021. Optimal Dual Schemes for Adaptive Grid Based Hexmeshing. arXiv:2103.07745 [cs.GR]
33. Marco Livesu, Alla Sheffer, Nicholas Vining, and Marco Tarini. 2015. Practical Hex-Mesh Optimization via Edge-Cone Rectification. ACM Transactions on Graphics (TOG) 34, 4 (2015), 141:1–141:11.
34. Marco Livesu, Nicholas Vining, Alla Sheffer, James Gregson, and Riccardo Scateni. 2013. PolyCut: monotone graph-cuts for PolyCube base-complex construction. ACM Transactions on Graphics (TOG) 32, 6 (2013), 171:1–171:12.
35. Loïc Maréchal. 2009. Advances in octree-based all-hexahedral mesh generation: handling sharp features. In Proc. 18th international meshing roundtable. Springer, 65–84.
36. Scott A Mitchell and Stephen A Vavasis. 1992. Quality mesh generation in three dimensions. In Proc. 8th annual symposium on Computational geometry. 212–221.
37. Steven J Owen. 1998. A survey of unstructured mesh generation technology. In Proc. 9th international meshing roundtable. 267–291.
38. Nicolas Ray, Dmitry Sokolov, Maxence Reberol, Franck Ledoux, and Bruno Lévy. 2018. Hex-dominant meshing: mind the gap! Computer-Aided Design 102 (2018), 94–103.
39. Teseo Schneider, Yixin Hu, Xifeng Gao, Jeremie Dumas, Denis Zorin, and Daniele Panozzo. 2019. A Large Scale Comparison of Tetrahedral and Hexahedral Elements for Finite Element Analysis. arXiv:1903.09332 [cs.NA]
40. Robert Schneiders. 1996. A grid-based algorithm for the generation of hexahedral element meshes. Engineering with computers 12, 3-4 (1996), 168–177.
41. Robert Schneiders. 1997. An algorithm for the generation of hexahedral element meshes based on an octree technique. In Proc. 6th International Meshing Roundtable. 195–196.
42. Robert Schneiders. 2000a. Algorithms for quadrilateral and hexahedral mesh generation. In Proc. VKI Lecture Series on Computational Fluid Dynamic. 2000–2004.
43. Robert Schneiders. 2000b. Octree-based hexahedral mesh generation. International Journal of Computational Geometry & Applications 10, 4 (2000), 383–398.
44. Robert Schneiders and Rolf Bünten. 1995. Automatic generation of hexahedral finite element meshes. Computer Aided Geometric Design 12, 7 (1995), 693–707.
45. Robert Schneiders, Roland Schindler, and Frank Weiler. 1996. Octree-based generation of hexahedral element meshes. In Proc. 5th International Meshing Roundtable. Sandia National Labs, 205–216.
46. Lior Shapira, Ariel Shamir, and Daniel Cohen-Or. 2008. Consistent mesh partitioning and skeletonisation using the shape diameter function. The Visual Computer 24, 4 (2008), 249.
47. Jason F Shepherd and Chris R Johnson. 2008. Hexahedral mesh generation constraints. Engineering with Computers 24, 3 (2008), 195–213.
48. Matthew L Staten, Robert A Kerr, Steven J Owen, Ted D Blacker, Marco Stupazzini, and Kenji Shimada. 2010. Unconstrained plastering—Hexahedral mesh generation via advancing-front geometry decomposition. Internat. J. Numer. Methods Engrg. 81, 2 (2010), 135–171.
49. Marco Tarini, Kai Hormann, Paolo Cignoni, and Claudio Montani. 2004. Polycube-maps. ACM Transactions on Graphics (TOG) 23, 3 (2004), 853–860.
50. Timothy J Tautges. 2001. The generation of hexahedral meshes for assembly geometry: survey and progress. Internat. J. Numer. Methods Engrg. 50, 12 (2001), 2617–2642.
51. Wei Wang, Yong Cao, and Tsubasa Okaze. 2021. Comparison of hexahedral, tetrahedral and polyhedral cells for reproducing the wind field around an isolated building by LES. Building and Environment 195 (2021), 107717.
52. Haiyan Wu, Shuming Gao, Rui Wang, and Jinming Chen. 2018. Fuzzy clustering based pseudo-swept volume decomposition for hexahedral meshing. Computer-Aided Design 96 (2018), 42–58.
53. Kaoji Xu, Xifeng Gao, Zhigang Deng, and Guoning Chen. 2017. Hexahedral meshing with varying element sizes. Computer Graphics Forum 36, 8 (2017), 540–553.
54. Yongjie Zhang and Chandrajit Bajaj. 2006. Adaptive and quality quadrilateral/hexahedral meshing from volumetric data. Computer methods in applied mechanics and engineering 195, 9-12 (2006), 942–960.