“Large steps in inverse rendering of geometry” by Nicolet, Jacobson and Jakob
Conference:
Type(s):
Title:
- Large steps in inverse rendering of geometry
Session/Category Title: Reconstruction
Presenter(s)/Author(s):
Abstract:
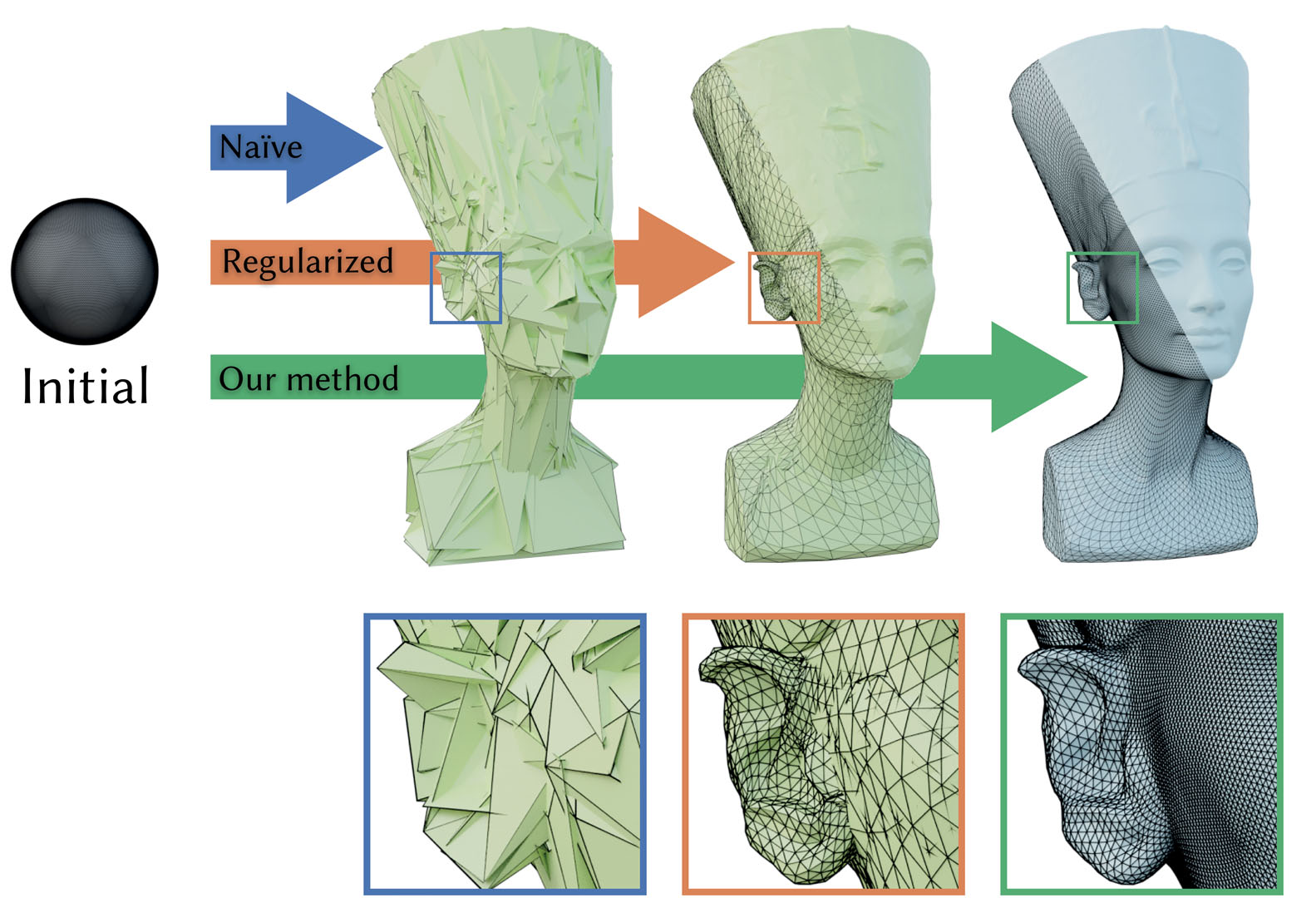
Inverse reconstruction from images is a central problem in many scientific and engineering disciplines. Recent progress on differentiable rendering has led to methods that can efficiently differentiate the full process of image formation with respect to millions of parameters to solve such problems via gradient-based optimization.At the same time, the availability of cheap derivatives does not necessarily make an inverse problem easy to solve. Mesh-based representations remain a particular source of irritation: an adverse gradient step involving vertex positions could turn parts of the mesh inside-out, introduce numerous local self-intersections, or lead to inadequate usage of the vertex budget due to distortion. These types of issues are often irrecoverable in the sense that subsequent optimization steps will further exacerbate them. In other words, the optimization lacks robustness due to an objective function with substantial non-convexity.Such robustness issues are commonly mitigated by imposing additional regularization, typically in the form of Laplacian energies that quantify and improve the smoothness of the current iterate. However, regularization introduces its own set of problems: solutions must now compromise between solving the problem and being smooth. Furthermore, gradient steps involving a Laplacian energy resemble Jacobi’s iterative method for solving linear equations that is known for its exceptionally slow convergence.We propose a simple and practical alternative that casts differentiable rendering into the framework of preconditioned gradient descent. Our pre-conditioner biases gradient steps towards smooth solutions without requiring the final solution to be smooth. In contrast to Jacobi-style iteration, each gradient step propagates information among all variables, enabling convergence using fewer and larger steps.Our method is not restricted to meshes and can also accelerate the reconstruction of other representations, where smooth solutions are generally expected. We demonstrate its superior performance in the context of geometric optimization and texture reconstruction.
References:
1. Sai Praveen Bangaru, Tzu-Mao Li, and Frédo Durand. 2020. Unbiased warped-area sampling for differentiable rendering. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1–18.
2. David Baraff and Andrew Witkin. 1998. Large Steps in Cloth Simulation. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’98). Association for Computing Machinery, New York, NY, USA, 43–54.
3. Mario Botsch and Leif Kobbelt. 2004a. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 23, 3 (2004), 630–634.
4. Mario Botsch and Leif Kobbelt. 2004b. A Remeshing Approach to Multiresolution Modeling. In Second Eurographics Symposium on Geometry Processing, Nice, France, July 8-10, 2004 (ACM International Conference Proceeding Series), Jean-Daniel Boissonnat and Pierre Alliez (Eds.), Vol. 71. Eurographics Association, 185–192.
5. Mario Botsch, Leif Kobbelt, Mark Pauly, Pierre Alliez, and Bruno Lévy. 2010. Polygon Mesh Processing. A K Peters. http://www.crcpress.com/product/isbn/9781568814261
6. Yanqing Chen, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. 2008. Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate. ACM Trans. Math. Softw. 35, 3, Article 22 (Oct. 2008).
7. Sebastian Claici, Mikhail Bessmeltsev, Scott Schaefer, and Justin Solomon. 2017. Isometry-Aware Preconditioning for Mesh Parameterization. Comput. Graph. Forum 36, 5 (2017), 37–47.
8. Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan H. Barr. 1999. Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1999, Los Angeles, CA, USA, August 8-13, 1999, Warren N. Waggenspack (Ed.). ACM, 317–324.
9. Gerhard Dziuk. 1988. Finite elements for the Beltrami operator on arbitrary surfaces. In Partial differential equations and calculus of variations. Springer, 142–155.
10. Kyle Genova, Forrester Cole, Aaron Maschinot, Aaron Sarna, Daniel Vlasic, and William T Freeman. 2018. Unsupervised training for 3d morphable model regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 8377–8386.
11. Ioannis Gkioulekas, Anat Levin, and Todd Zickler. 2016. An evaluation of computational imaging techniques for heterogeneous inverse scattering. In European Conference on Computer Vision. Springer, 685–701.
12. Andreas Griewank and Andrea Walther. 2008. Evaluating derivatives: principles and techniques of algorithmic differentiation. SIAM.
13. Alec Jacobson, Elif Tosun, Olga Sorkine, and Denis Zorin. 2010. Mixed Finite Elements for Variational Surface Modeling. Comput. Graph. Forum 29, 5 (2010), 1565–1574.
14. J. Karátson and L. Lóczi. 2005. Sobolev Gradient Preconditioning for the Electrostatic Potential Equation. Comp. and Math. with App. (2005).
15. Hiroharu Kato, Yoshitaka Ushiku, and Tatsuya Harada. 2018. Neural 3d mesh renderer. In Proceedings of the IEEE conference on computer vision and pattern recognition. 3907–3916.
16. Michael Kazhdan, Jake Solomon, and Mirela Ben-Chen. 2012. Can Mean-Curvature Flow be Modified to be Non-singular? Comput. Graph. Forum 31, 5 (2012), 1745–1754.
17. Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
18. Shahar Z. Kovalsky, Meirav Galun, and Yaron Lipman. 2016. Accelerated Quadratic Proxy for Geometric Optimization. ACM Transactions on Graphics (proceedings of ACM SIGGRAPH) (2016).
19. Samuli Laine, Janne Hellsten, Tero Karras, Yeongho Seol, Jaakko Lehtinen, and Timo Aila. 2020. Modular primitives for high-performance differentiable rendering. ACM Transactions on Graphics (TOG) 39, 6 (2020), 1–14.
20. Tzu-Mao Li, Miika Aittala, Frédo Durand, and Jaakko Lehtinen. 2018. Differentiable monte carlo ray tracing through edge sampling. ACM Transactions on Graphics (TOG) 37, 6 (2018), 1–11.
21. Yaron Lipman, Olga Sorkine, Daniel Cohen-Or, David Levin, Christian Rössl, and Hans-Peter Seidel. 2004. Differential Coordinates for Interactive Mesh Editing. In 2004 International Conference on Shape Modeling and Applications (SMI 2004), 7-9 June 2004, Genova, Italy. IEEE Computer Society, 181–190. 2004.1314505
22. Hsueh-Ti Derek Liu, Michael Tao, and Alec Jacobson. 2018. Paparazzi: surface editing by way of multi-view image processing. ACM Trans. Graph. 37, 6 (2018), 221:1–221:11.
23. Shichen Liu, Tianye Li, Weikai Chen, and Hao Li. 2019. Soft rasterizer: A differentiable renderer for image-based 3d reasoning. In Proceedings of the IEEE International Conference on Computer Vision. 7708–7717.
24. Matthew M Loper and Michael J Black. 2014. OpenDR: An approximate differentiable renderer. In European Conference on Computer Vision. Springer, 154–169.
25. Guillaume Loubet, Nicolas Holzschuch, and Wenzel Jakob. 2019. Reparameterizing discontinuous integrands for differentiable rendering. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1–14.
26. Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. 2020. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision. Springer, 405–421.
27. Maxim Naumov. 2011. Parallel solution of sparse triangular linear systems in the preconditioned iterative methods on the GPU. NVIDIA Corp., Westford, MA, USA, Tech. Rep. NVR-2011 1 (2011).
28. Andrew Nealen, Takeo Igarashi, Olga Sorkine, and Marc Alexa. 2006. Laplacian mesh optimization. In Proceedings of the 4th International Conference on Computer Graphics and Interactive Techniques in Australasia and Southeast Asia 2006, Kuala Lumpur, Malaysia, November 29 – December 2, 2006, Y. T. Lee, Siti Mariyam Hj. Shamsuddin, Diego Gutierrez, and Norhaida Mohd. Suaib (Eds.). ACM, 381–389.
29. J. W. Neuberger. 1985. Steepest descent and differential equations. Journal of the Mathematical Society of Japan 37, 2 (1985), 187 — 195.
30. Merlin Nimier-David, Sébastien Speierer, Benoît Ruiz, and Wenzel Jakob. 2020. Radiative backpropagation: an adjoint method for lightning-fast differentiable rendering. ACM Transactions on Graphics (TOG) 39, 4 (2020), 146–1.
31. Merlin Nimier-David, Delio Vicini, Tizian Zeltner, and Wenzel Jakob. 2019. Mitsuba 2: A retargetable forward and inverse renderer. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1–17.
32. Stanley J. Osher, Bao Wang, Penghang Yin, Xiyang Luo, Minh Pham, and Alex Tong Lin. 2018. Laplacian Smoothing Gradient Descent. CoRR abs/1806.06317 (2018). arXiv:1806.06317 http://arxiv.org/abs/1806.06317
33. Jea-Hyun Park, Abner J. Salgado, and Steven M. Wise. 2021. Preconditioned accelerated gradient descent methods for locally Lipschitz smooth objectives with applications to the solution of nonlinear PDEs. arXiv:math.NA/2006.06732
34. Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. 2019. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, and R. Garnett (Eds.). Curran Associates, Inc., 8024–8035. http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf
35. Gustavo Patow and Xavier Pueyo. 2003. A survey of inverse rendering problems. In Computer graphics forum, Vol. 22. Wiley Online Library, 663–687.
36. Ulrich Pinkall and Konrad Polthier. 1993. Computing discrete minimal surfaces and their conjugates. Experimental mathematics 2, 1 (1993), 15–36.
37. Michael Rabinovich, Roi Poranne, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Scalable Locally Injective Mappings. ACM Trans. Graph. 36, 2, Article 16 (April 2017), 16 pages.
38. Ravi Ramamoorthi and Pat Hanrahan. 2001. An efficient representation for irradiance environment maps. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques. 497–500.
39. Nikhila Ravi, Jeremy Reizenstein, David Novotny, Taylor Gordon, Wan-Yen Lo, Justin Johnson, and Georgia Gkioxari. 2020. Accelerating 3D Deep Learning with PyTorch3D. arXiv:2007.08501 (2020).
40. Justin Solomon, Keegan Crane, and Etienne Vouga. 2014. Laplace-Beltrami: The Swiss army knife of geometry processing. In Symposium on Geometry Processing graduate school (Cardiff, UK, 2014), Vol. 2.
41. Olga Sorkine. 2005. Laplacian Mesh Processing. In Eurographics, State of the Art Report. 53–70.
42. Olga Sorkine. 2006. Differential representations for mesh processing. In Computer Graphics Forum, Vol. 25. Wiley Online Library, 789–807.
43. Demetri Terzopoulos, Andrew Witkin, and Michael Kass. 1988. Constraints on deformable models: Recovering 3D shape and nonrigid motion. Artificial intelligence 36, 1 (1988), 91–123.
44. Delio Vicini, Sébastien Speierer, and Wenzel Jakob. 2021. Path Replay Backpropagation: Differentiating Light Paths using Constant Memory and Linear Time. Transactions on Graphics (Proceedings of SIGGRAPH) 40, 4 (Aug. 2021), 108:1–108:14.
45. Yu Wang and Justin Solomon. 2021. Fast quasi-harmonic weights for geometric data interpolation. ACM Trans. Graph. 40, 4 (2021), 73:1–73:15.
46. Udaranga Wickramasinghe, Pascal Fua, and Graham Knott. 2021. Deep Active Surface Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 11652–11661.
47. Chris Yu, Henrik Schumacher, and Keenan Crane. 2021. Repulsive Curves. ACM Trans. Graph. 40, 2 (2021).
48. Tizian Zeltner, Sébastien Speierer, Iliyan Georgiev, and Wenzel Jakob. 2021. Monte Carlo Estimators for Differential Light Transport. Transactions on Graphics (Proceedings of SIGGRAPH) 40, 4 (Aug. 2021).
49. Cheng Zhang, Zhao Dong, Michael Doggett, and Shuang Zhao. 2021. Antithetic Sampling for Monte Carlo Differentiable Rendering. ACM Trans. Graph. 40, 4 (2021), 77:1–77:12.
50. Cheng Zhang, Bailey Miller, Kai Yan, Ioannis Gkioulekas, and Shuang Zhao. 2020. Path-Space Differentiable Rendering. ACM Trans. Graph. 39, 4 (July 2020).
51. Cheng Zhang, Lifan Wu, Changxi Zheng, Ioannis Gkioulekas, Ravi Ramamoorthi, and Shuang Zhao. 2019. A differential theory of radiative transfer. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1–16.
52. Yufeng Zhu, Robert Bridson, and Danny M. Kaufman. 2018. Blended Cured Quasi-Newton for Distortion Optimization. to appear ACM Trans. on Graphics (SIGGRAPH 2018) (2018).